On Applications of Bootstrap in Continuous Space Reinforcement Learning

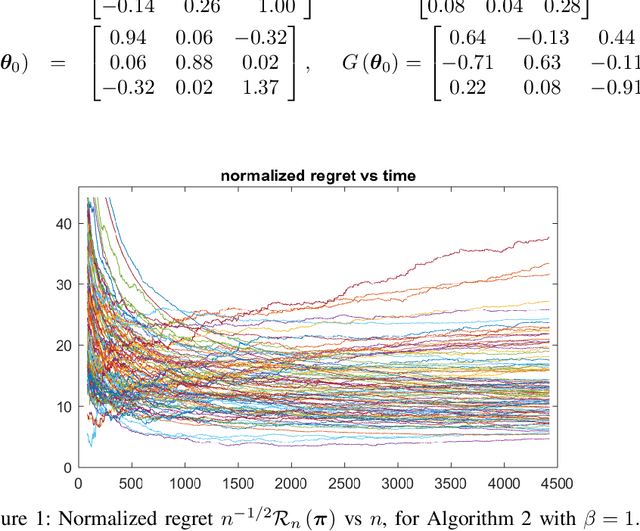
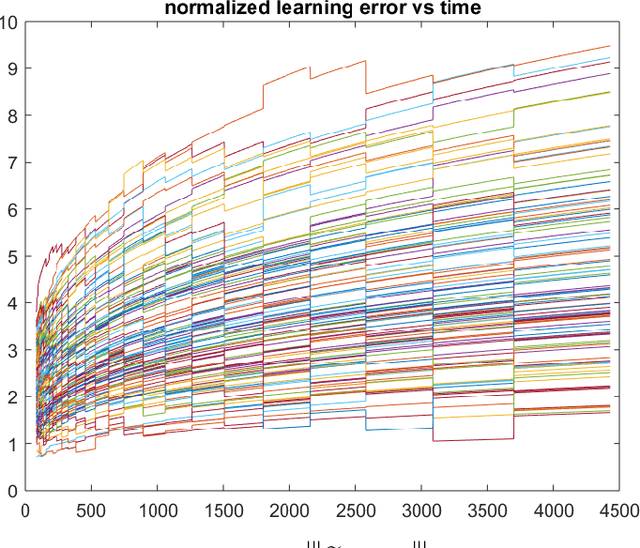
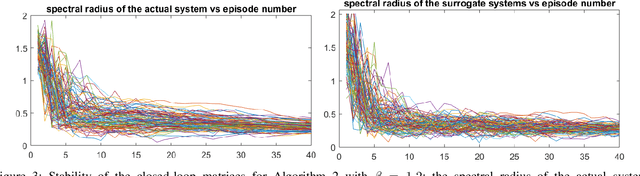
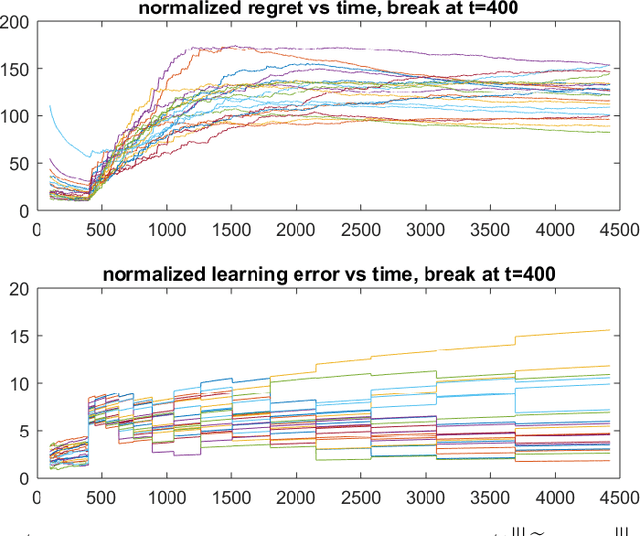
In decision making problems for continuous state and action spaces, linear dynamical models are widely employed. Specifically, policies for stochastic linear systems subject to quadratic cost functions capture a large number of applications in reinforcement learning. Selected randomized policies have been studied in the literature recently that address the trade-off between identification and control. However, little is known about policies based on bootstrapping observed states and actions. In this work, we show that bootstrap-based policies achieve a square root scaling of regret with respect to time. We also obtain results on the accuracy of learning the model's dynamics. Corroborative numerical analysis that illustrates the technical results is also provided.

On the Optimality of Perturbations in Stochastic and Adversarial Multi-armed Bandit Problems

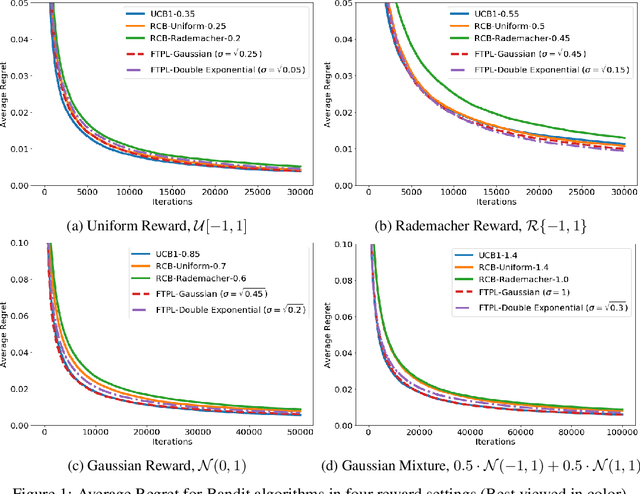
We investigate the optimality of perturbation based algorithms in the stochastic and adversarial multi-armed bandit problems. For the stochastic case, we provide a unified analysis for all sub-Weibull perturbations. The sub-Weibull family includes sub-Gaussian and sub-Exponential distributions. Our bounds are instance optimal for a range of the sub-Weibull parameter. For the adversarial setting, we prove rigorous barriers against two natural solution approaches using tools from discrete choice theory and extreme value theory. Our results suggest that the optimal perturbation, if it exists, will be of Frechet-type.

Input Perturbations for Adaptive Regulation and Learning

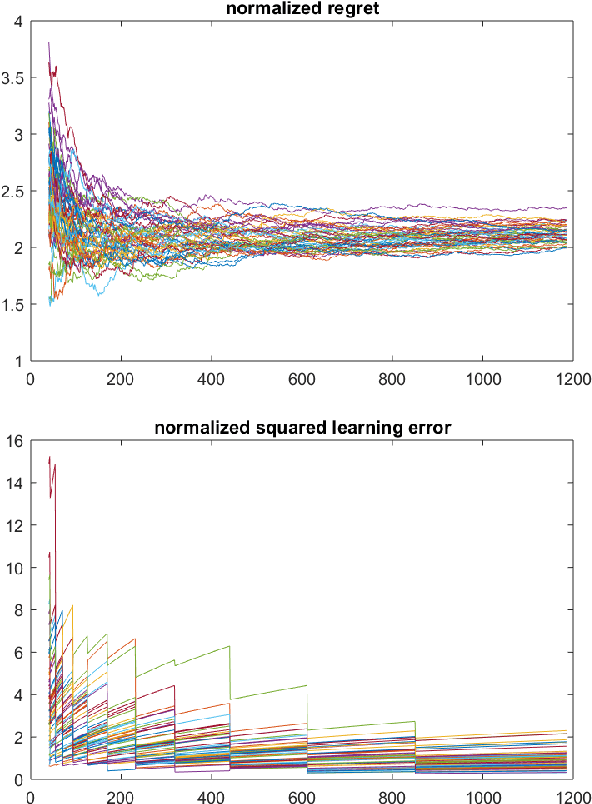
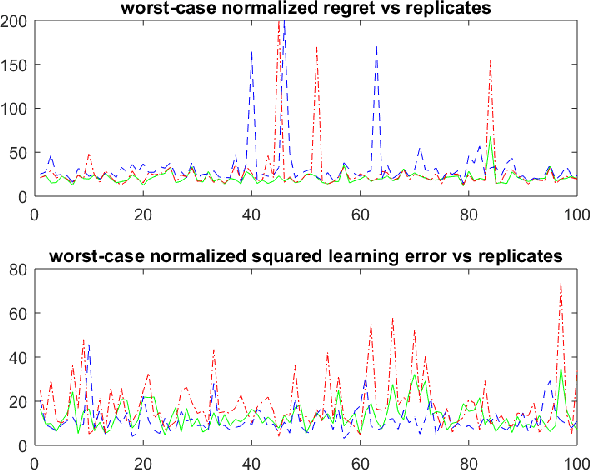
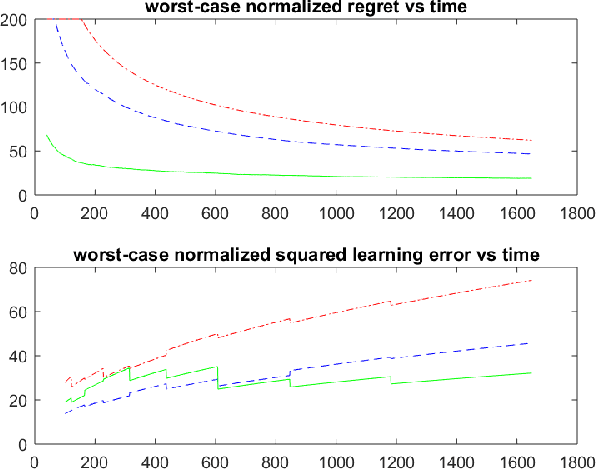
Design of adaptive algorithms for simultaneous regulation and estimation of MIMO linear dynamical systems is a canonical reinforcement learning problem. Efficient policies whose regret (i.e. increase in the cost due to uncertainty) scales at a square-root rate of time have been studied extensively in the recent literature. Nevertheless, existing strategies are computationally intractable and require a priori knowledge of key system parameters. The only exception is a randomized Greedy regulator, for which asymptotic regret bounds have been recently established. However, randomized Greedy leads to probable fluctuations in the trajectory of the system, which renders its finite time regret suboptimal. This work addresses the above issues by designing policies that utilize input signals perturbations. We show that perturbed Greedy guarantees non-asymptotic regret bounds of (nearly) square-root magnitude w.r.t. time. More generally, we establish high probability bounds on both the regret and the learning accuracy under arbitrary input perturbations. The settings where Greedy attains the information theoretic lower bound of logarithmic regret are also discussed. To obtain the results, state-of-the-art tools from martingale theory together with the recently introduced method of policy decomposition are leveraged. Beside adaptive regulators, analysis of input perturbations captures key applications including remote sensing and distributed control.

Online Multiclass Boosting with Bandit Feedback

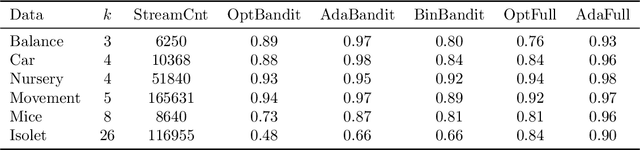
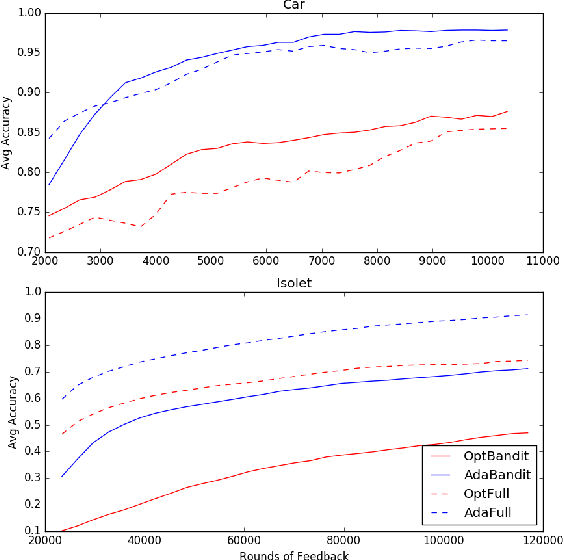
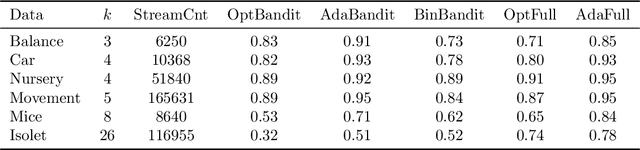
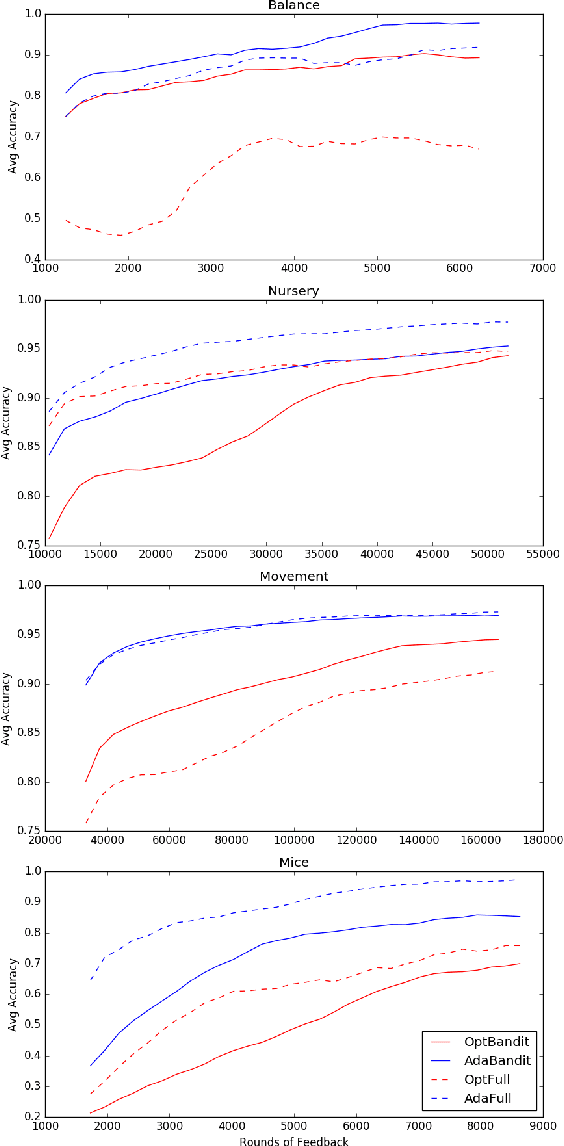
We present online boosting algorithms for multiclass classification with bandit feedback, where the learner only receives feedback about the correctness of its prediction. We propose an unbiased estimate of the loss using a randomized prediction, allowing the model to update its weak learners with limited information. Using the unbiased estimate, we extend two full information boosting algorithms (Jung et al., 2017) to the bandit setting. We prove that the asymptotic error bounds of the bandit algorithms exactly match their full information counterparts. The cost of restricted feedback is reflected in the larger sample complexity. Experimental results also support our theoretical findings, and performance of the proposed models is comparable to the that of an existing bandit boosting algorithm, which is limited to use binary weak learners.

Fighting Contextual Bandits with Stochastic Smoothing

We introduce a new stochastic smoothing perspective to study adversarial contextual bandit problems. We propose a general algorithm template that represents random perturbation based algorithms and identify several perturbation distributions that lead to strong regret bounds. Using the idea of smoothness, we provide an $O(\sqrt{T})$ zero-order bound for the vanilla algorithm and an $O(L^{*2/3}_{T})$ first-order bound for the clipped version. These bounds hold when the algorithms use with a variety of distributions that have a bounded hazard rate. Our algorithm template includes EXP4 as a special case corresponding to the Gumbel perturbation. Our regret bounds match existing results for EXP4 without relying on the specific properties of the algorithm.

Random ReLU Features: Universality, Approximation, and Composition

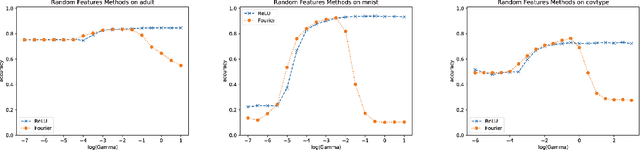
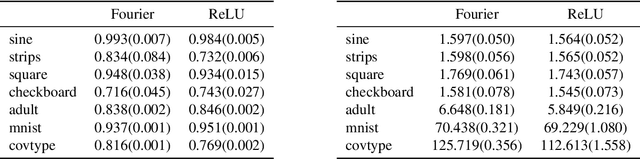
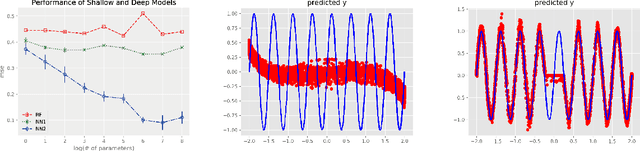
We propose random ReLU features models in this work. Its motivation is rooted in both kernel methods and neural networks. We prove the universality and generalization performance of random ReLU features. Parallel to Barron's theorem, we consider the ReLU feature class, extended from the reproducing kernel Hilbert space of random ReLU features, and prove a strong quantitative approximation theorem, where both inner weights and outer weights of the the neural network with ReLU nodes as an approximator are bounded by constants. We also prove a similar approximation theorem for composition of functions in ReLU feature class by multi-layer ReLU networks. Separation theorem between ReLU feature class and their composition is proved as a consequence of separation between shallow and deep networks. These results reveal nice properties of ReLU nodes from the view of approximation theory, providing support for regularization on weights of ReLU networks and for the use of random ReLU features in practice. Our experiments confirm that the performance of random ReLU features is comparable with random Fourier features.

But How Does It Work in Theory? Linear SVM with Random Features

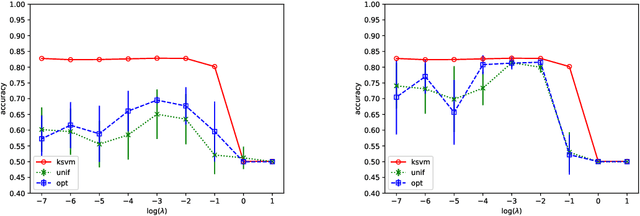
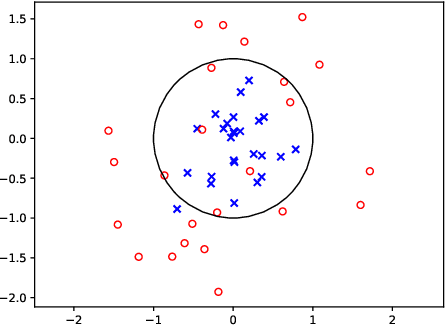
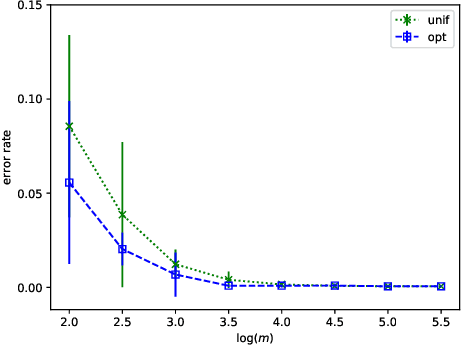
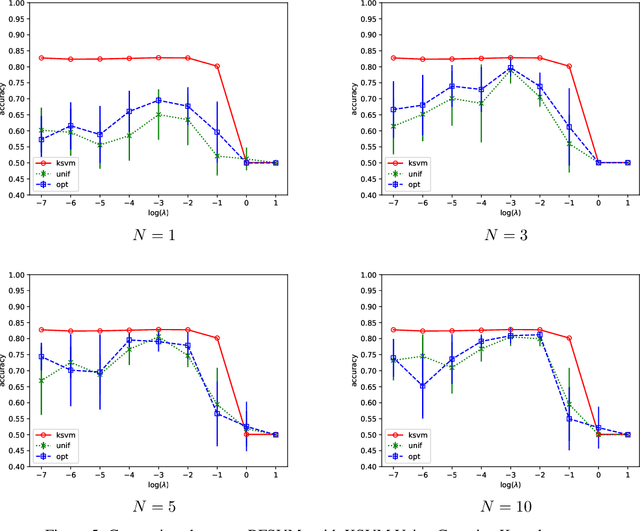
We prove that, under low noise assumptions, the support vector machine with $N\ll m$ random features (RFSVM) can achieve the learning rate faster than $O(1/\sqrt{m})$ on a training set with $m$ samples when an optimized feature map is used. Our work extends the previous fast rate analysis of random features method from least square loss to 0-1 loss. We also show that the reweighted feature selection method, which approximates the optimized feature map, helps improve the performance of RFSVM in experiments on a synthetic data set.

Regret Analysis for Adaptive Linear-Quadratic Policies

In the classical problem of Linear-Quadratic (LQ) control, when the parameters of the system's dynamics are unknown, an adaptive policy is needed to learn those parameters and also plan a control action. The resulting trade-off between accurate parameter estimation (exploration) and effective control (exploitation) represents the main challenge in the area of adaptive control. Asymptotic approaches have been extensively studied in the literature, but there is a dearth of non-asymptotic results that in addition are rather incomplete. This study establishes high probability regret bounds for the aforementioned problem that are optimal up to logarithmic factors. The results on finite time analysis of the regret are obtained under very mild assumptions, requiring: (i) stabilizability of the system's dynamics, and (ii) limiting the degree of heaviness of the noise distribution. To establish such bounds, certain novel techniques are introduced to comprehensively address the probabilistic behavior of dependent random matrices with heavy-tailed distributions.

Finite Time Adaptive Stabilization of LQ Systems

Stabilization of linear systems with unknown dynamics is a canonical problem in adaptive control. Since the lack of knowledge of system parameters can cause it to become destabilized, an adaptive stabilization procedure is needed prior to regulation. Therefore, the adaptive stabilization needs to be completed in finite time. In order to achieve this goal, asymptotic approaches are not very helpful. There are only a few existing non-asymptotic results and a full treatment of the problem is not currently available. In this work, leveraging the novel method of random linear feedbacks, we establish high probability guarantees for finite time stabilization. Our results hold for remarkably general settings because we carefully choose a minimal set of assumptions. These include stabilizability of the underlying system and restricting the degree of heaviness of the noise distribution. To derive our results, we also introduce a number of new concepts and technical tools to address regularity and instability of the closed-loop matrix.

Online Boosting Algorithms for Multi-label Ranking

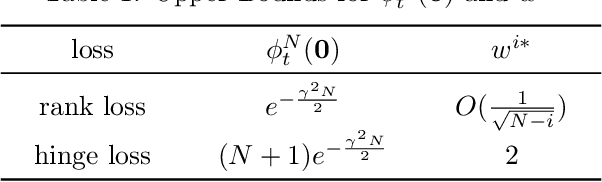
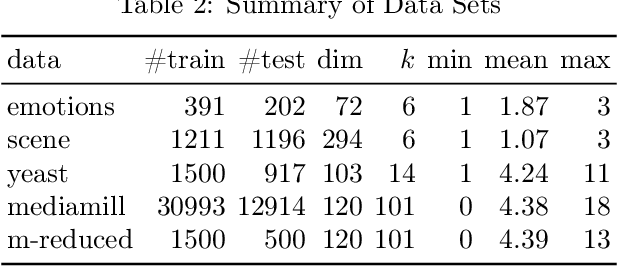
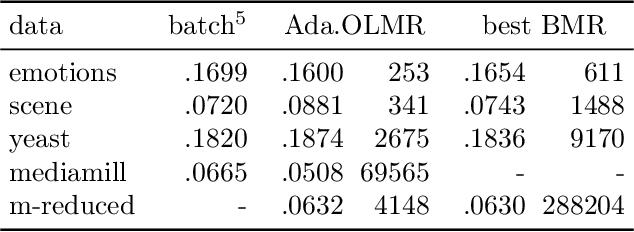
We consider the multi-label ranking approach to multi-label learning. Boosting is a natural method for multi-label ranking as it aggregates weak predictions through majority votes, which can be directly used as scores to produce a ranking of the labels. We design online boosting algorithms with provable loss bounds for multi-label ranking. We show that our first algorithm is optimal in terms of the number of learners required to attain a desired accuracy, but it requires knowledge of the edge of the weak learners. We also design an adaptive algorithm that does not require this knowledge and is hence more practical. Experimental results on real data sets demonstrate that our algorithms are at least as good as existing batch boosting algorithms.