Revisiting the Necessity of Graph Learning and Common Graph Benchmarks

Graph machine learning has enjoyed a meteoric rise in popularity since the introduction of deep learning in graph contexts. This is no surprise due to the ubiquity of graph data in large scale industrial settings. Tacitly assumed in all graph learning tasks is the separation of the graph structure and node features: node features strictly encode individual data while the graph structure consists only of pairwise interactions. The driving belief is that node features are (by themselves) insufficient for these tasks, so benchmark performance accurately reflects improvements in graph learning. In our paper, we challenge this orthodoxy by showing that, surprisingly, node features are oftentimes more-than-sufficient for many common graph benchmarks, breaking this critical assumption. When comparing against a well-tuned feature-only MLP baseline on seven of the most commonly used graph learning datasets, one gains little benefit from using graph structure on five datasets. We posit that these datasets do not benefit considerably from graph learning because the features themselves already contain enough graph information to obviate or substantially reduce the need for the graph. To illustrate this point, we perform a feature study on these datasets and show how the features are responsible for closing the gap between MLP and graph-method performance. Further, in service of introducing better empirical measures of progress for graph neural networks, we present a challenging parametric family of principled synthetic datasets that necessitate graph information for nontrivial performance. Lastly, we section out a subset of real-world datasets that are not trivially solved by an MLP and hence serve as reasonable benchmarks for graph neural networks.

Shedding Light on Problems with Hyperbolic Graph Learning

Recent papers in the graph machine learning literature have introduced a number of approaches for hyperbolic representation learning. The asserted benefits are improved performance on a variety of graph tasks, node classification and link prediction included. Claims have also been made about the geometric suitability of particular hierarchical graph datasets to representation in hyperbolic space. Despite these claims, our work makes a surprising discovery: when simple Euclidean models with comparable numbers of parameters are properly trained in the same environment, in most cases, they perform as well, if not better, than all introduced hyperbolic graph representation learning models, even on graph datasets previously claimed to be the most hyperbolic as measured by Gromov $\delta$-hyperbolicity (i.e., perfect trees). This observation gives rise to a simple question: how can this be? We answer this question by taking a careful look at the field of hyperbolic graph representation learning as it stands today, and find that a number of papers fail to diligently present baselines, make faulty modelling assumptions when constructing algorithms, and use misleading metrics to quantify geometry of graph datasets. We take a closer look at each of these three problems, elucidate the issues, perform an analysis of methods, and introduce a parametric family of benchmark datasets to ascertain the applicability of (hyperbolic) graph neural networks.

Wasserstein Wormhole: Scalable Optimal Transport Distance with Transformers

Optimal transport (OT) and the related Wasserstein metric (W) are powerful and ubiquitous tools for comparing distributions. However, computing pairwise Wasserstein distances rapidly becomes intractable as cohort size grows. An attractive alternative would be to find an embedding space in which pairwise Euclidean distances map to OT distances, akin to standard multidimensional scaling (MDS). We present Wasserstein Wormhole, a transformer-based autoencoder that embeds empirical distributions into a latent space wherein Euclidean distances approximate OT distances. Extending MDS theory, we show that our objective function implies a bound on the error incurred when embedding non-Euclidean distances. Empirically, distances between Wormhole embeddings closely match Wasserstein distances, enabling linear time computation of OT distances. Along with an encoder that maps distributions to embeddings, Wasserstein Wormhole includes a decoder that maps embeddings back to distributions, allowing for operations in the embedding space to generalize to OT spaces, such as Wasserstein barycenter estimation and OT interpolation. By lending scalability and interpretability to OT approaches, Wasserstein Wormhole unlocks new avenues for data analysis in the fields of computational geometry and single-cell biology.

Random ReLU Features: Universality, Approximation, and Composition

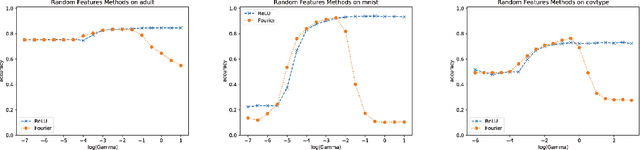
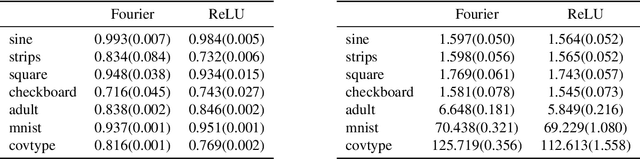
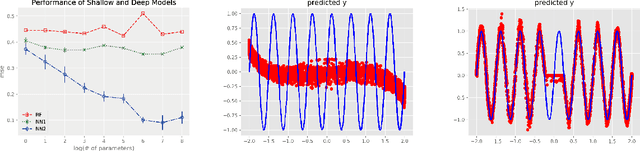
We propose random ReLU features models in this work. Its motivation is rooted in both kernel methods and neural networks. We prove the universality and generalization performance of random ReLU features. Parallel to Barron's theorem, we consider the ReLU feature class, extended from the reproducing kernel Hilbert space of random ReLU features, and prove a strong quantitative approximation theorem, where both inner weights and outer weights of the the neural network with ReLU nodes as an approximator are bounded by constants. We also prove a similar approximation theorem for composition of functions in ReLU feature class by multi-layer ReLU networks. Separation theorem between ReLU feature class and their composition is proved as a consequence of separation between shallow and deep networks. These results reveal nice properties of ReLU nodes from the view of approximation theory, providing support for regularization on weights of ReLU networks and for the use of random ReLU features in practice. Our experiments confirm that the performance of random ReLU features is comparable with random Fourier features.

But How Does It Work in Theory? Linear SVM with Random Features

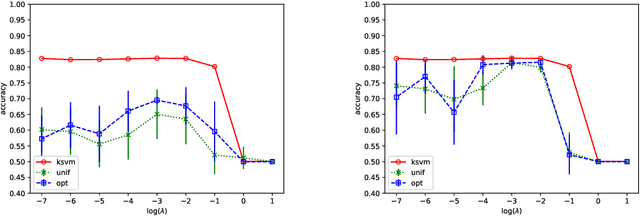
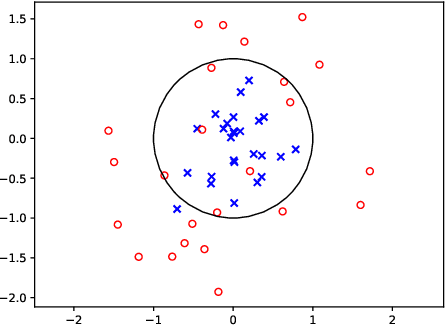
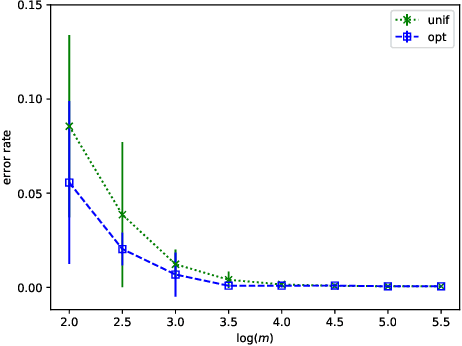
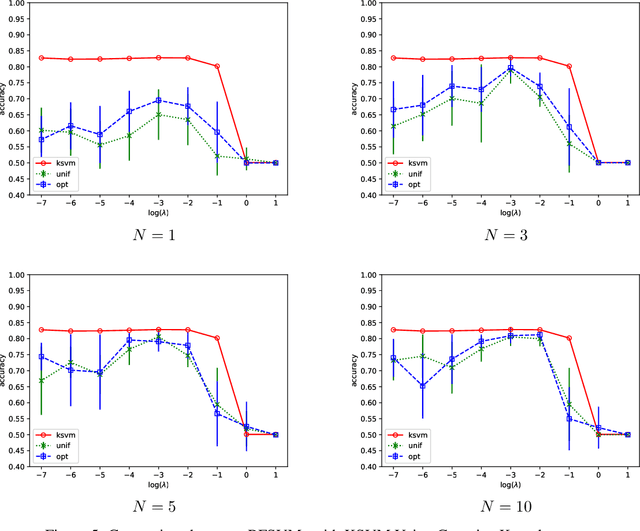
We prove that, under low noise assumptions, the support vector machine with $N\ll m$ random features (RFSVM) can achieve the learning rate faster than $O(1/\sqrt{m})$ on a training set with $m$ samples when an optimized feature map is used. Our work extends the previous fast rate analysis of random features method from least square loss to 0-1 loss. We also show that the reweighted feature selection method, which approximates the optimized feature map, helps improve the performance of RFSVM in experiments on a synthetic data set.