Data Amplification: A Unified and Competitive Approach to Property Estimation

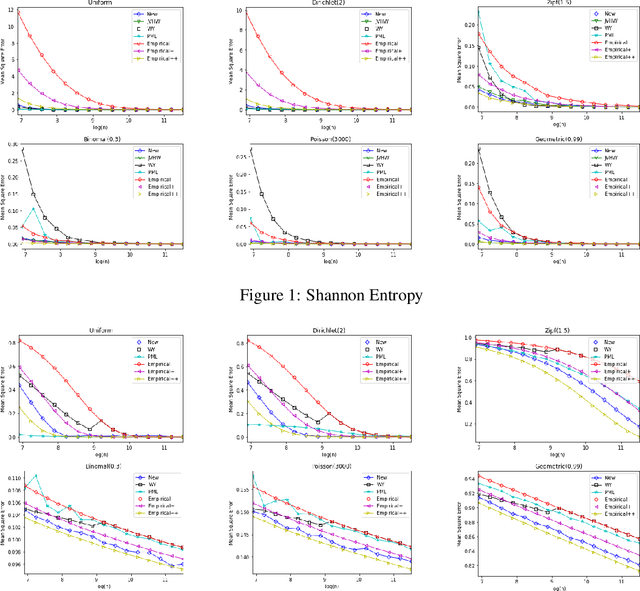
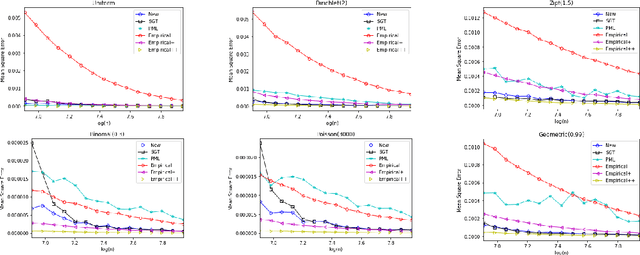
Estimating properties of discrete distributions is a fundamental problem in statistical learning. We design the first unified, linear-time, competitive, property estimator that for a wide class of properties and for all underlying distributions uses just $2n$ samples to achieve the performance attained by the empirical estimator with $n\sqrt{\log n}$ samples. This provides off-the-shelf, distribution-independent, "amplification" of the amount of data available relative to common-practice estimators. We illustrate the estimator's practical advantages by comparing it to existing estimators for a wide variety of properties and distributions. In most cases, its performance with $n$ samples is even as good as that of the empirical estimator with $n\log n$ samples, and for essentially all properties, its performance is comparable to that of the best existing estimator designed specifically for that property.

Data Amplification: Instance-Optimal Property Estimation

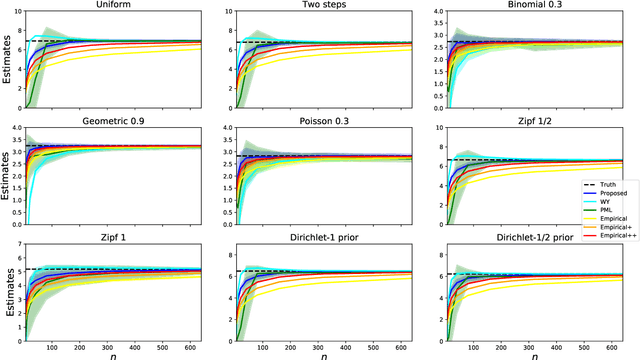
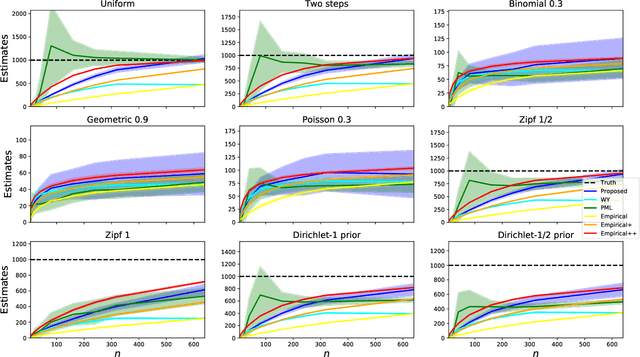
The best-known and most commonly used distribution-property estimation technique uses a plug-in estimator, with empirical frequency replacing the underlying distribution. We present novel linear-time-computable estimators that significantly "amplify" the effective amount of data available. For a large variety of distribution properties including four of the most popular ones and for every underlying distribution, they achieve the accuracy that the empirical-frequency plug-in estimators would attain using a logarithmic-factor more samples. Specifically, for Shannon entropy and a very broad class of properties including $\ell_1$-distance, the new estimators use $n$ samples to achieve the accuracy attained by the empirical estimators with $n\log n$ samples. For support-size and coverage, the new estimators use $n$ samples to achieve the performance of empirical frequency with sample size $n$ times the logarithm of the property value. Significantly strengthening the traditional min-max formulation, these results hold not only for the worst distributions, but for each and every underlying distribution. Furthermore, the logarithmic amplification factors are optimal. Experiments on a wide variety of distributions show that the new estimators outperform the previous state-of-the-art estimators designed for each specific property.

On Learning Markov Chains

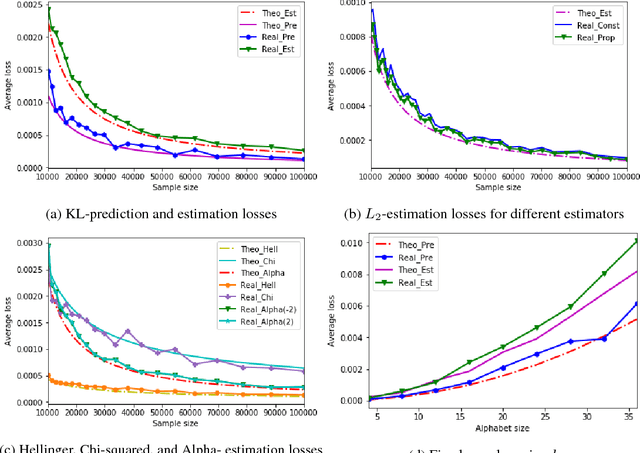
The problem of estimating an unknown discrete distribution from its samples is a fundamental tenet of statistical learning. Over the past decade, it attracted significant research effort and has been solved for a variety of divergence measures. Surprisingly, an equally important problem, estimating an unknown Markov chain from its samples, is still far from understood. We consider two problems related to the min-max risk (expected loss) of estimating an unknown $k$-state Markov chain from its $n$ sequential samples: predicting the conditional distribution of the next sample with respect to the KL-divergence, and estimating the transition matrix with respect to a natural loss induced by KL or a more general $f$-divergence measure. For the first measure, we determine the min-max prediction risk to within a linear factor in the alphabet size, showing it is $\Omega(k\log\log n\ / n)$ and $\mathcal{O}(k^2\log\log n\ / n)$. For the second, if the transition probabilities can be arbitrarily small, then only trivial uniform risk upper bounds can be derived. We therefore consider transition probabilities that are bounded away from zero, and resolve the problem for essentially all sufficiently smooth $f$-divergences, including KL-, $L_2$-, Chi-squared, Hellinger, and Alpha-divergences.

Maximum Selection and Ranking under Noisy Comparisons

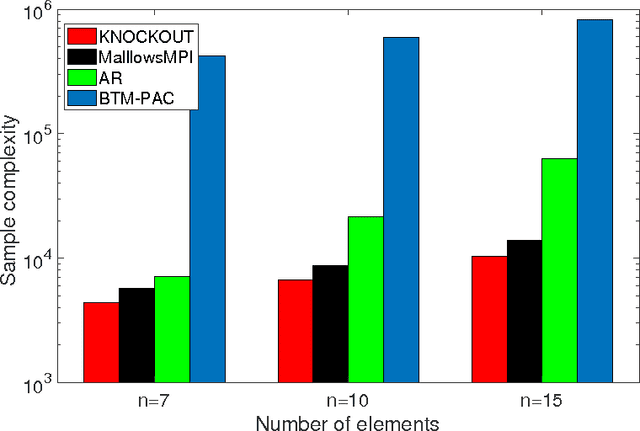
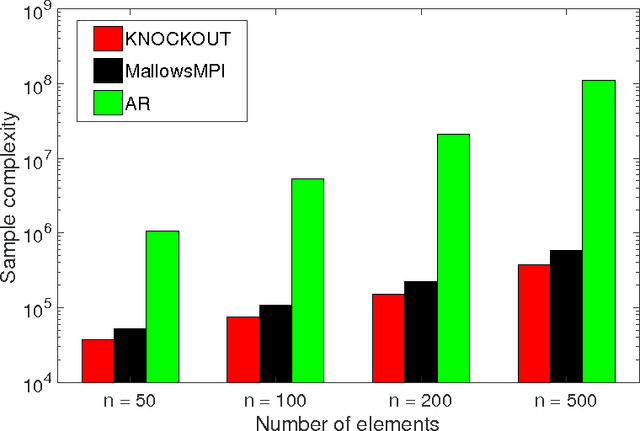
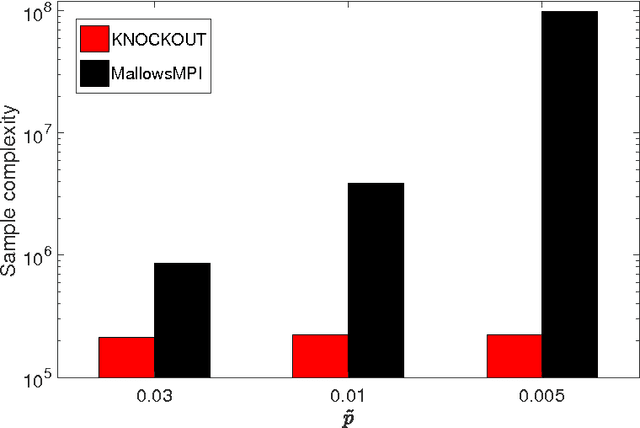
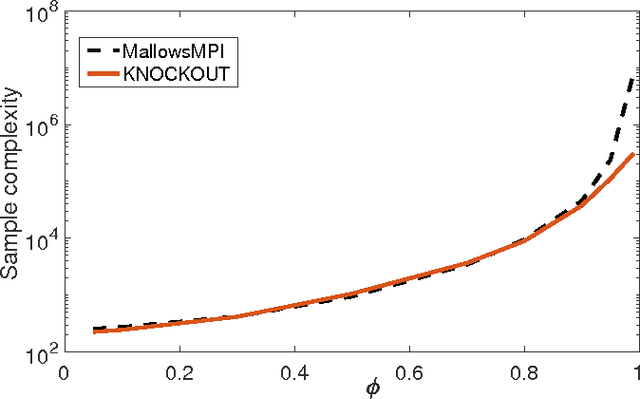
We consider $(\epsilon,\delta)$-PAC maximum-selection and ranking for general probabilistic models whose comparisons probabilities satisfy strong stochastic transitivity and stochastic triangle inequality. Modifying the popular knockout tournament, we propose a maximum-selection algorithm that uses $\mathcal{O}\left(\frac{n}{\epsilon^2}\log \frac{1}{\delta}\right)$ comparisons, a number tight up to a constant factor. We then derive a general framework that improves the performance of many ranking algorithms, and combine it with merge sort and binary search to obtain a ranking algorithm that uses $\mathcal{O}\left(\frac{n\log n (\log \log n)^3}{\epsilon^2}\right)$ comparisons for any $\delta\ge\frac1n$, a number optimal up to a $(\log \log n)^3$ factor.

A Unified Maximum Likelihood Approach for Optimal Distribution Property Estimation

The advent of data science has spurred interest in estimating properties of distributions over large alphabets. Fundamental symmetric properties such as support size, support coverage, entropy, and proximity to uniformity, received most attention, with each property estimated using a different technique and often intricate analysis tools. We prove that for all these properties, a single, simple, plug-in estimator---profile maximum likelihood (PML)---performs as well as the best specialized techniques. This raises the possibility that PML may optimally estimate many other symmetric properties.

Estimating Renyi Entropy of Discrete Distributions

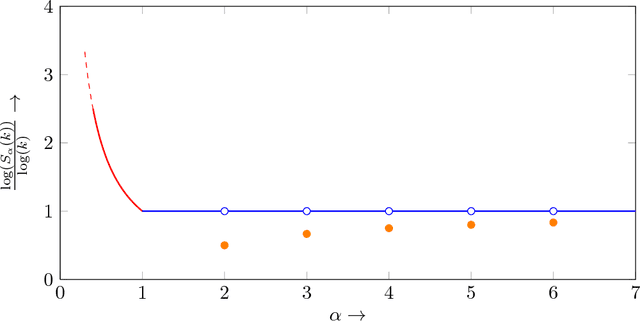
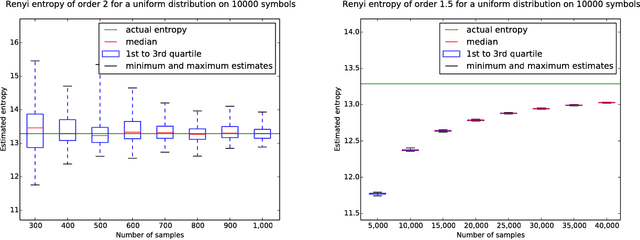
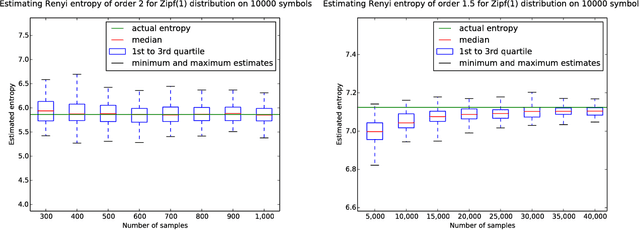
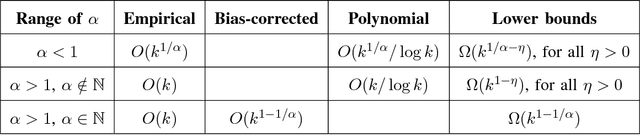
It was recently shown that estimating the Shannon entropy $H({\rm p})$ of a discrete $k$-symbol distribution ${\rm p}$ requires $\Theta(k/\log k)$ samples, a number that grows near-linearly in the support size. In many applications $H({\rm p})$ can be replaced by the more general R\'enyi entropy of order $\alpha$, $H_\alpha({\rm p})$. We determine the number of samples needed to estimate $H_\alpha({\rm p})$ for all $\alpha$, showing that $\alpha < 1$ requires a super-linear, roughly $k^{1/\alpha}$ samples, noninteger $\alpha>1$ requires a near-linear $k$ samples, but, perhaps surprisingly, integer $\alpha>1$ requires only $\Theta(k^{1-1/\alpha})$ samples. Furthermore, developing on a recently established connection between polynomial approximation and estimation of additive functions of the form $\sum_{x} f({\rm p}_x)$, we reduce the sample complexity for noninteger values of $\alpha$ by a factor of $\log k$ compared to the empirical estimator. The estimators achieving these bounds are simple and run in time linear in the number of samples. Our lower bounds provide explicit constructions of distributions with different R\'enyi entropies that are hard to distinguish.

Estimating the number of unseen species: A bird in the hand is worth $\log n $ in the bush

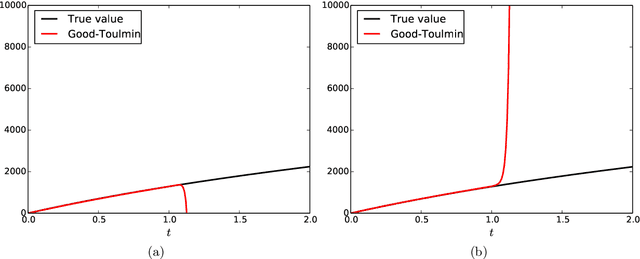
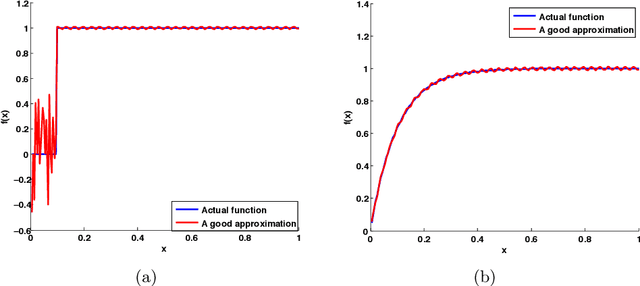
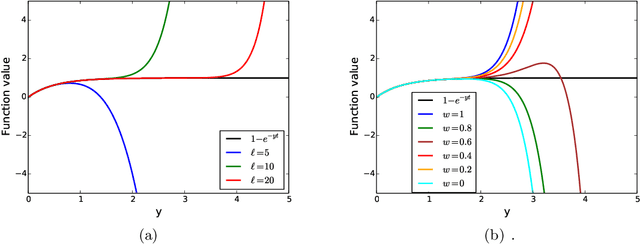
Estimating the number of unseen species is an important problem in many scientific endeavors. Its most popular formulation, introduced by Fisher, uses $n$ samples to predict the number $U$ of hitherto unseen species that would be observed if $t\cdot n$ new samples were collected. Of considerable interest is the largest ratio $t$ between the number of new and existing samples for which $U$ can be accurately predicted. In seminal works, Good and Toulmin constructed an intriguing estimator that predicts $U$ for all $t\le 1$, thereby showing that the number of species can be estimated for a population twice as large as that observed. Subsequently Efron and Thisted obtained a modified estimator that empirically predicts $U$ even for some $t>1$, but without provable guarantees. We derive a class of estimators that $\textit{provably}$ predict $U$ not just for constant $t>1$, but all the way up to $t$ proportional to $\log n$. This shows that the number of species can be estimated for a population $\log n$ times larger than that observed, a factor that grows arbitrarily large as $n$ increases. We also show that this range is the best possible and that the estimators' mean-square error is optimal up to constants for any $t$. Our approach yields the first provable guarantee for the Efron-Thisted estimator and, in addition, a variant which achieves stronger theoretical and experimental performance than existing methodologies on a variety of synthetic and real datasets. The estimators we derive are simple linear estimators that are computable in time proportional to $n$. The performance guarantees hold uniformly for all distributions, and apply to all four standard sampling models commonly used across various scientific disciplines: multinomial, Poisson, hypergeometric, and Bernoulli product.

Faster Algorithms for Testing under Conditional Sampling

There has been considerable recent interest in distribution-tests whose run-time and sample requirements are sublinear in the domain-size $k$. We study two of the most important tests under the conditional-sampling model where each query specifies a subset $S$ of the domain, and the response is a sample drawn from $S$ according to the underlying distribution. For identity testing, which asks whether the underlying distribution equals a specific given distribution or $\epsilon$-differs from it, we reduce the known time and sample complexities from $\tilde{\mathcal{O}}(\epsilon^{-4})$ to $\tilde{\mathcal{O}}(\epsilon^{-2})$, thereby matching the information theoretic lower bound. For closeness testing, which asks whether two distributions underlying observed data sets are equal or different, we reduce existing complexity from $\tilde{\mathcal{O}}(\epsilon^{-4} \log^5 k)$ to an even sub-logarithmic $\tilde{\mathcal{O}}(\epsilon^{-5} \log \log k)$ thus providing a better bound to an open problem in Bertinoro Workshop on Sublinear Algorithms [Fisher, 2004].

Competitive Distribution Estimation

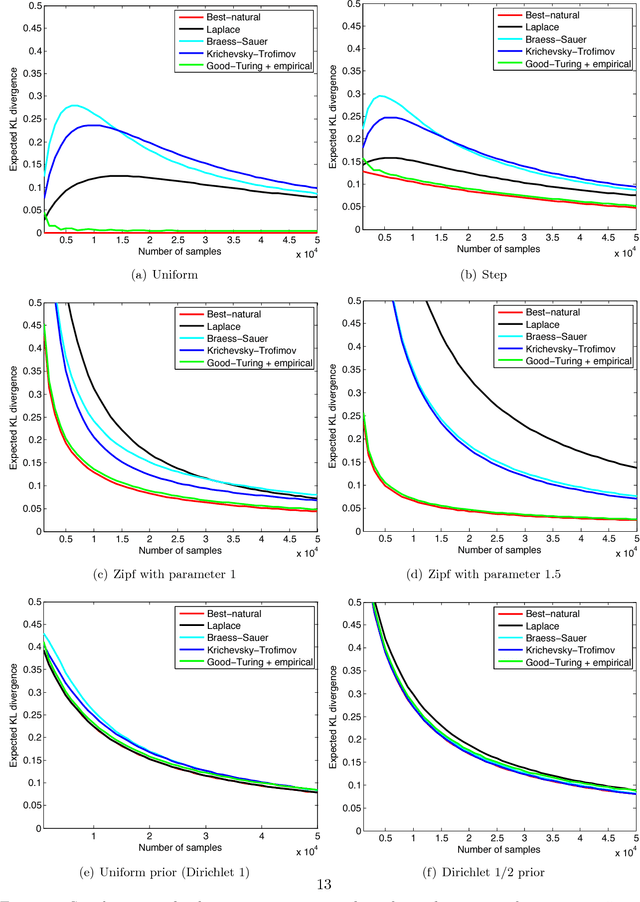
Estimating an unknown distribution from its samples is a fundamental problem in statistics. The common, min-max, formulation of this goal considers the performance of the best estimator over all distributions in a class. It shows that with $n$ samples, distributions over $k$ symbols can be learned to a KL divergence that decreases to zero with the sample size $n$, but grows unboundedly with the alphabet size $k$. Min-max performance can be viewed as regret relative to an oracle that knows the underlying distribution. We consider two natural and modest limits on the oracle's power. One where it knows the underlying distribution only up to symbol permutations, and the other where it knows the exact distribution but is restricted to use natural estimators that assign the same probability to symbols that appeared equally many times in the sample. We show that in both cases the competitive regret reduces to $\min(k/n,\tilde{\mathcal{O}}(1/\sqrt n))$, a quantity upper bounded uniformly for every alphabet size. This shows that distributions can be estimated nearly as well as when they are essentially known in advance, and nearly as well as when they are completely known in advance but need to be estimated via a natural estimator. We also provide an estimator that runs in linear time and incurs competitive regret of $\tilde{\mathcal{O}}(\min(k/n,1/\sqrt n))$, and show that for natural estimators this competitive regret is inevitable. We also demonstrate the effectiveness of competitive estimators using simulations.

Universal Compression of Envelope Classes: Tight Characterization via Poisson Sampling

The Poisson-sampling technique eliminates dependencies among symbol appearances in a random sequence. It has been used to simplify the analysis and strengthen the performance guarantees of randomized algorithms. Applying this method to universal compression, we relate the redundancies of fixed-length and Poisson-sampled sequences, use the relation to derive a simple single-letter formula that approximates the redundancy of any envelope class to within an additive logarithmic term. As a first application, we consider i.i.d. distributions over a small alphabet as a step-envelope class, and provide a short proof that determines the redundancy of discrete distributions over a small al- phabet up to the first order terms. We then show the strength of our method by applying the formula to tighten the existing bounds on the redundancy of exponential and power-law classes, in particular answering a question posed by Boucheron, Garivier and Gassiat.