ORBIT: Preserving Foundational Language Capabilities in GenRetrieval via Origin-Regulated Merging

Despite the rapid advancements in large language model (LLM) development, fine-tuning them for specific tasks often results in the catastrophic forgetting of their general, language-based reasoning abilities. This work investigates and addresses this challenge in the context of the Generative Retrieval (GenRetrieval) task. During GenRetrieval fine-tuning, we find this forgetting occurs rapidly and correlates with the distance between the fine-tuned and original model parameters. Given these observations, we propose ORBIT, a novel approach that actively tracks the distance between fine-tuned and initial model weights, and uses a weight averaging strategy to constrain model drift during GenRetrieval fine-tuning when this inter-model distance exceeds a maximum threshold. Our results show that ORBIT retains substantial text and retrieval performance by outperforming both common continual learning baselines and related regularization methods that also employ weight averaging.

PLUM: Adapting Pre-trained Language Models for Industrial-scale Generative Recommendations

Large Language Models (LLMs) pose a new paradigm of modeling and computation for information tasks. Recommendation systems are a critical application domain poised to benefit significantly from the sequence modeling capabilities and world knowledge inherent in these large models. In this paper, we introduce PLUM, a framework designed to adapt pre-trained LLMs for industry-scale recommendation tasks. PLUM consists of item tokenization using Semantic IDs, continued pre-training (CPT) on domain-specific data, and task-specific fine-tuning for recommendation objectives. For fine-tuning, we focus particularly on generative retrieval, where the model is directly trained to generate Semantic IDs of recommended items based on user context. We conduct comprehensive experiments on large-scale internal video recommendation datasets. Our results demonstrate that PLUM achieves substantial improvements for retrieval compared to a heavily-optimized production model built with large embedding tables. We also present a scaling study for the model's retrieval performance, our learnings about CPT, a few enhancements to Semantic IDs, along with an overview of the training and inference methods that enable launching this framework to billions of users in YouTube.

Stochastic Frank-Wolfe for Constrained Finite-Sum Minimization

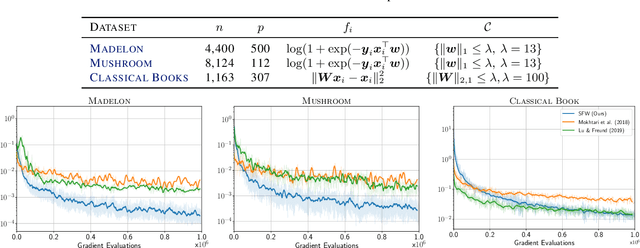
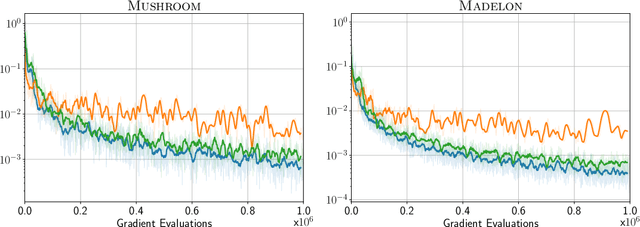
We propose a novel Stochastic Frank-Wolfe (a.k.a. Conditional Gradient) algorithm with a fixed batch size tailored to the constrained optimization of a finite sum of smooth objectives. The design of our method hinges on a primal-dual interpretation of the Frank-Wolfe algorithm. Recent work to design stochastic variants of the Frank-Wolfe algorithm falls into two categories: algorithms with increasing batch size, and algorithms with a given, constant, batch size. The former have faster convergence rates but are impractical; the latter are practical but slower. The proposed method combines the advantages of both: it converges for unit batch size, and has faster theoretical worst-case rates than previous unit batch size algorithms. Our experiments also show faster empirical convergence than previous unit batch size methods for several tasks. Finally, we construct a stochastic estimator of the Frank-Wolfe gap. It allows us to bound the true Frank-Wolfe gap, which in the convex setting bounds the primal-dual gap in the convex case while in general is a measure of stationarity. Our gap estimator can therefore be used as a practical stopping criterion in all cases.