Asynchronous adaptive networks

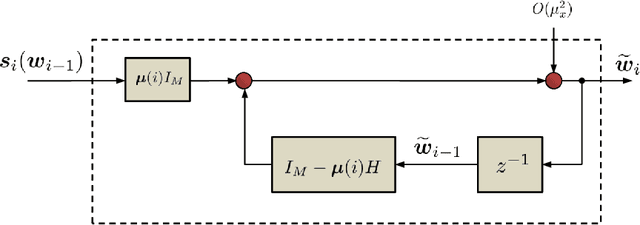
In a recent article [1] we surveyed advances related to adaptation, learning, and optimization over synchronous networks. Various distributed strategies were discussed that enable a collection of networked agents to interact locally in response to streaming data and to continually learn and adapt to track drifts in the data and models. Under reasonable technical conditions on the data, the adaptive networks were shown to be mean-square stable in the slow adaptation regime, and their mean-square-error performance and convergence rate were characterized in terms of the network topology and data statistical moments [2]. Classical results for single-agent adaptation and learning were recovered as special cases. Following the works [3]-[5], this chapter complements the exposition from [1] and extends the results to asynchronous networks. The operation of this class of networks can be subject to various sources of uncertainties that influence their dynamic behavior, including randomly changing topologies, random link failures, random data arrival times, and agents turning on and off randomly. In an asynchronous environment, agents may stop updating their solutions or may stop sending or receiving information in a random manner and without coordination with other agents. The presentation will reveal that the mean-square-error performance of asynchronous networks remains largely unaltered compared to synchronous networks. The results justify the remarkable resilience of cooperative networks in the face of random events.

Performance Limits of Stochastic Sub-Gradient Learning, Part I: Single Agent Case

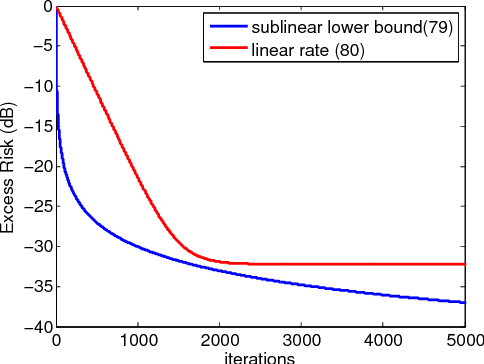
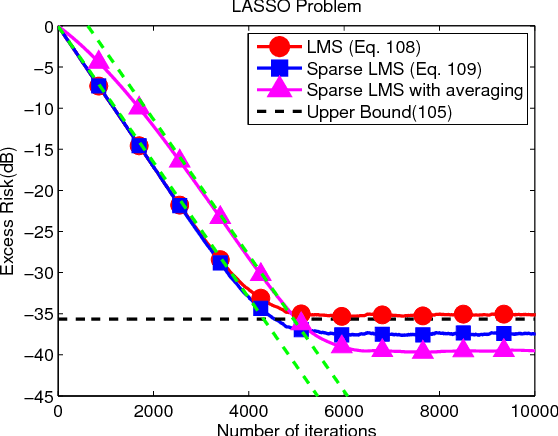
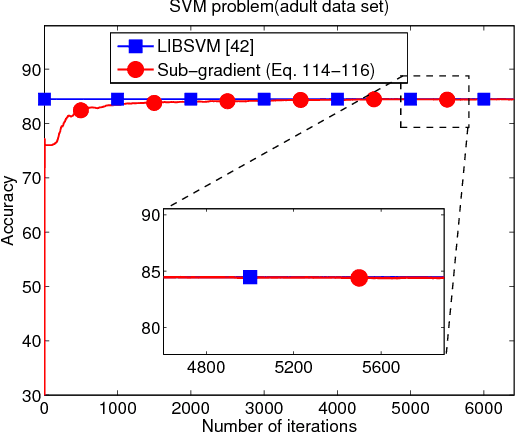
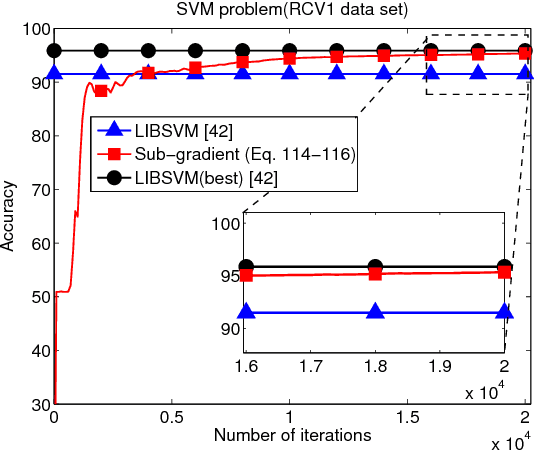
In this work and the supporting Part II, we examine the performance of stochastic sub-gradient learning strategies under weaker conditions than usually considered in the literature. The new conditions are shown to be automatically satisfied by several important cases of interest including SVM, LASSO, and Total-Variation denoising formulations. In comparison, these problems do not satisfy the traditional assumptions used in prior analyses and, therefore, conclusions derived from these earlier treatments are not directly applicable to these problems. The results in this article establish that stochastic sub-gradient strategies can attain linear convergence rates, as opposed to sub-linear rates, to the steady-state regime. A realizable exponential-weighting procedure is employed to smooth the intermediate iterates and guarantee useful performance bounds in terms of convergence rate and excessive risk performance. Part I of this work focuses on single-agent scenarios, which are common in stand-alone learning applications, while Part II extends the analysis to networked learners. The theoretical conclusions are illustrated by several examples and simulations, including comparisons with the FISTA procedure.

Performance Limits of Stochastic Sub-Gradient Learning, Part II: Multi-Agent Case

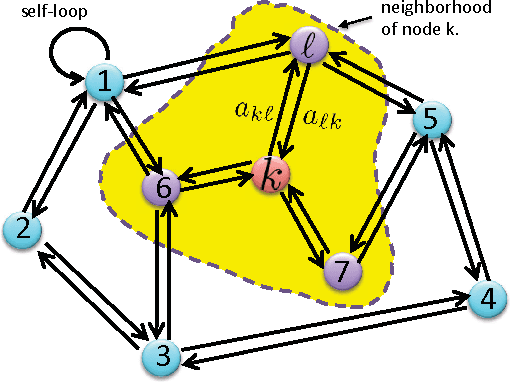
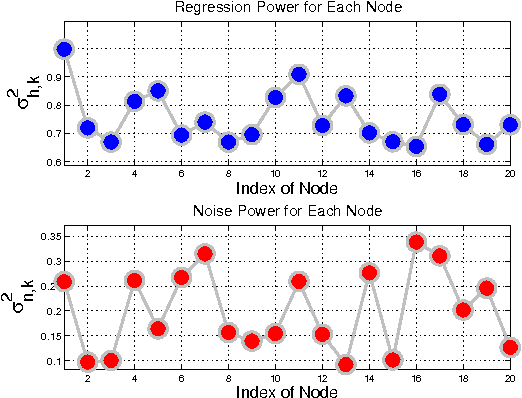
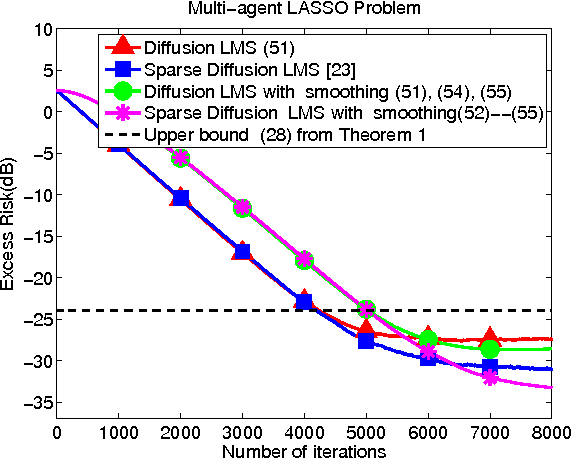
The analysis in Part I revealed interesting properties for subgradient learning algorithms in the context of stochastic optimization when gradient noise is present. These algorithms are used when the risk functions are non-smooth and involve non-differentiable components. They have been long recognized as being slow converging methods. However, it was revealed in Part I that the rate of convergence becomes linear for stochastic optimization problems, with the error iterate converging at an exponential rate $\alpha^i$ to within an $O(\mu)-$neighborhood of the optimizer, for some $\alpha \in (0,1)$ and small step-size $\mu$. The conclusion was established under weaker assumptions than the prior literature and, moreover, several important problems (such as LASSO, SVM, and Total Variation) were shown to satisfy these weaker assumptions automatically (but not the previously used conditions from the literature). These results revealed that sub-gradient learning methods have more favorable behavior than originally thought when used to enable continuous adaptation and learning. The results of Part I were exclusive to single-agent adaptation. The purpose of the current Part II is to examine the implications of these discoveries when a collection of networked agents employs subgradient learning as their cooperative mechanism. The analysis will show that, despite the coupled dynamics that arises in a networked scenario, the agents are still able to attain linear convergence in the stochastic case; they are also able to reach agreement within $O(\mu)$ of the optimizer.

Multitask diffusion adaptation over networks with common latent representations

Online learning with streaming data in a distributed and collaborative manner can be useful in a wide range of applications. This topic has been receiving considerable attention in recent years with emphasis on both single-task and multitask scenarios. In single-task adaptation, agents cooperate to track an objective of common interest, while in multitask adaptation agents track multiple objectives simultaneously. Regularization is one useful technique to promote and exploit similarity among tasks in the latter scenario. This work examines an alternative way to model relations among tasks by assuming that they all share a common latent feature representation. As a result, a new multitask learning formulation is presented and algorithms are developed for its solution in a distributed online manner. We present a unified framework to analyze the mean-square-error performance of the adaptive strategies, and conduct simulations to illustrate the theoretical findings and potential applications.

Decentralized Clustering and Linking by Networked Agents

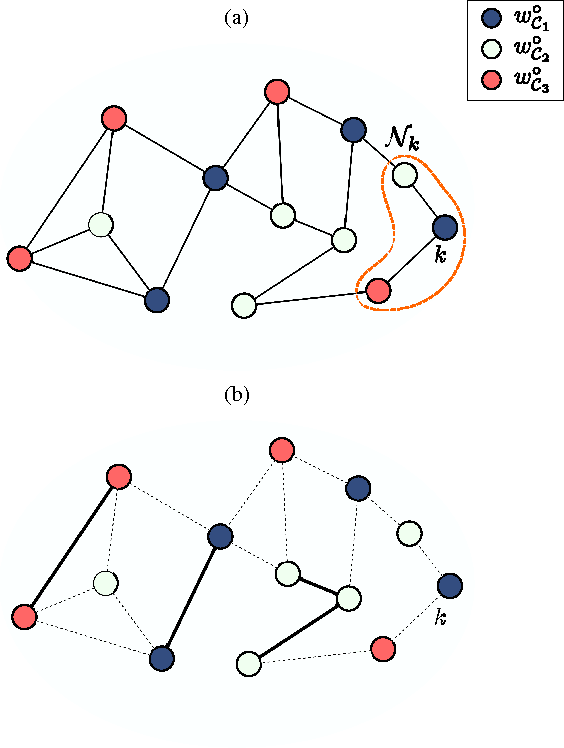
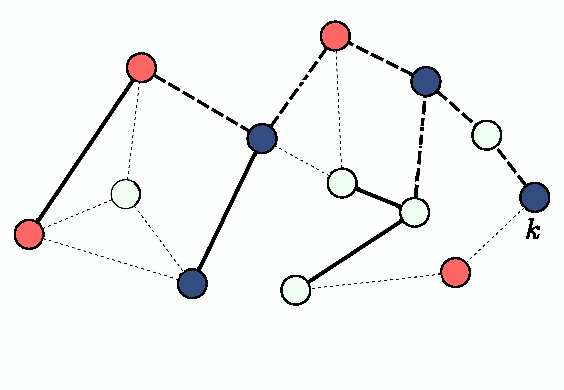
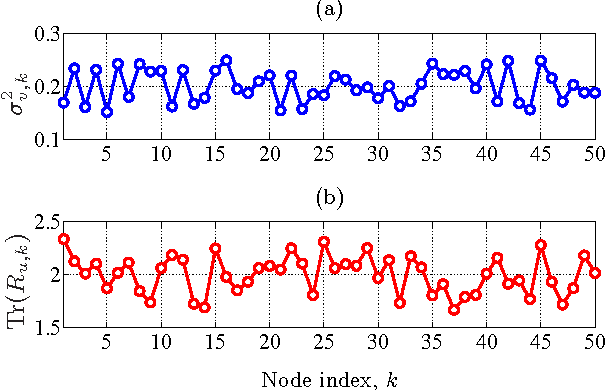
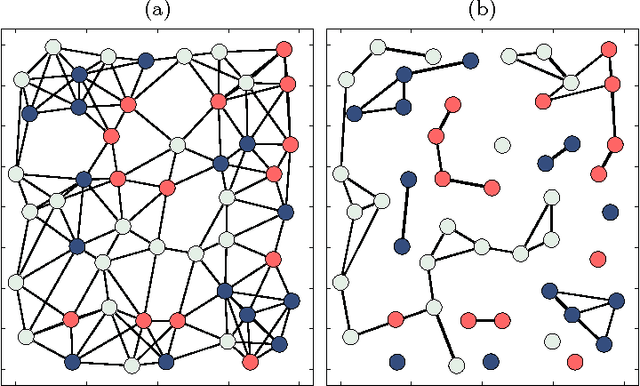
We consider the problem of decentralized clustering and estimation over multi-task networks, where agents infer and track different models of interest. The agents do not know beforehand which model is generating their own data. They also do not know which agents in their neighborhood belong to the same cluster. We propose a decentralized clustering algorithm aimed at identifying and forming clusters of agents of similar objectives, and at guiding cooperation to enhance the inference performance. One key feature of the proposed technique is the integration of the learning and clustering tasks into a single strategy. We analyze the performance of the procedure and show that the error probabilities of types I and II decay exponentially to zero with the step-size parameter. While links between agents following different objectives are ignored in the clustering process, we nevertheless show how to exploit these links to relay critical information across the network for enhanced performance. Simulation results illustrate the performance of the proposed method in comparison to other useful techniques.

On the Influence of Momentum Acceleration on Online Learning

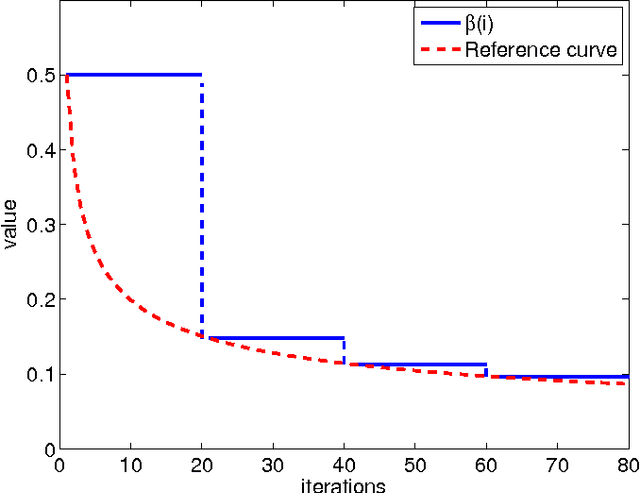
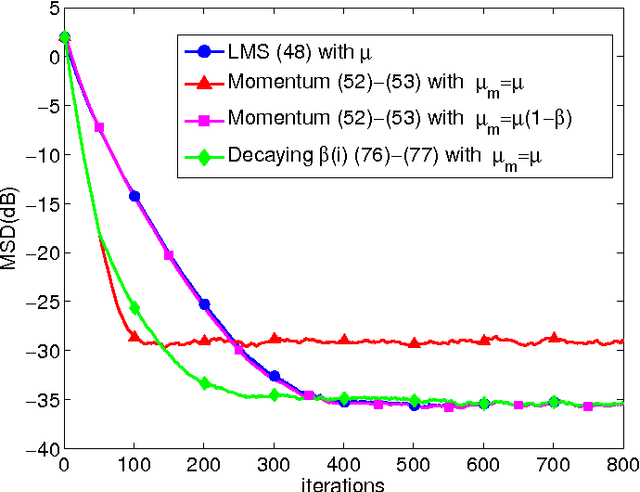
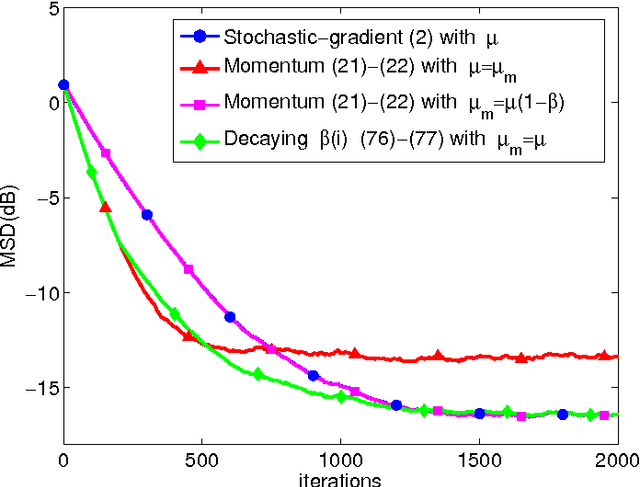
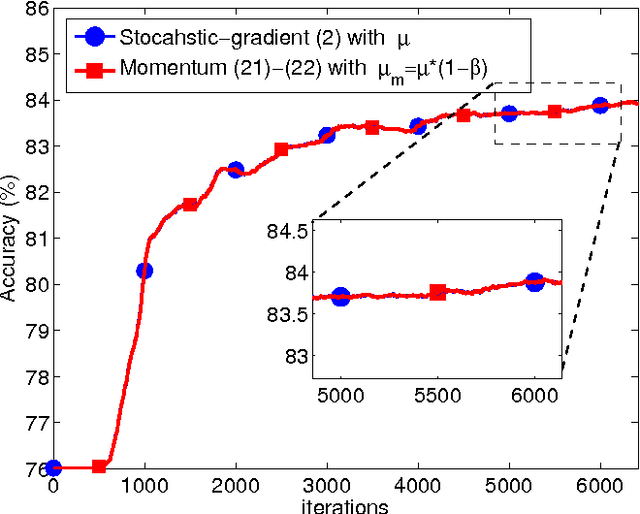
The article examines in some detail the convergence rate and mean-square-error performance of momentum stochastic gradient methods in the constant step-size and slow adaptation regime. The results establish that momentum methods are equivalent to the standard stochastic gradient method with a re-scaled (larger) step-size value. The size of the re-scaling is determined by the value of the momentum parameter. The equivalence result is established for all time instants and not only in steady-state. The analysis is carried out for general strongly convex and smooth risk functions, and is not limited to quadratic risks. One notable conclusion is that the well-known bene ts of momentum constructions for deterministic optimization problems do not necessarily carry over to the adaptive online setting when small constant step-sizes are used to enable continuous adaptation and learn- ing in the presence of persistent gradient noise. From simulations, the equivalence between momentum and standard stochastic gradient methods is also observed for non-differentiable and non-convex problems.

Online Dual Coordinate Ascent Learning

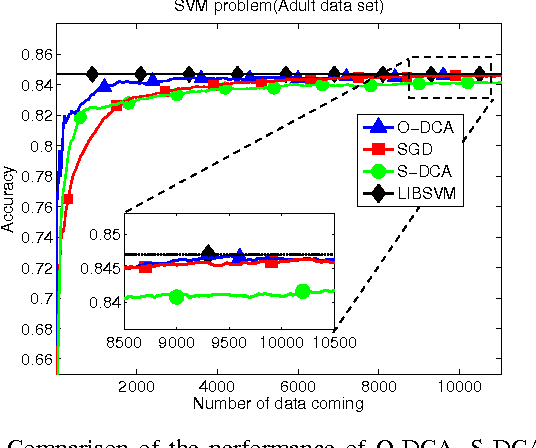
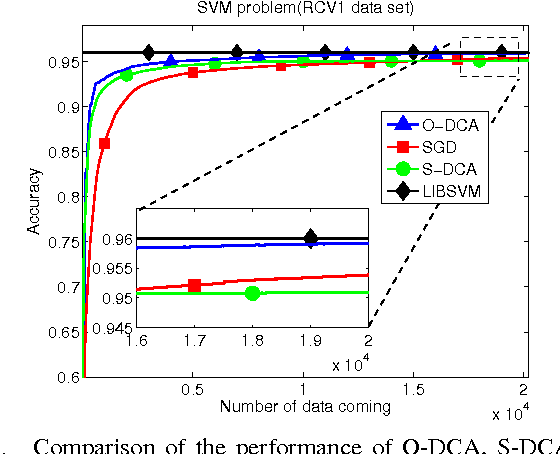
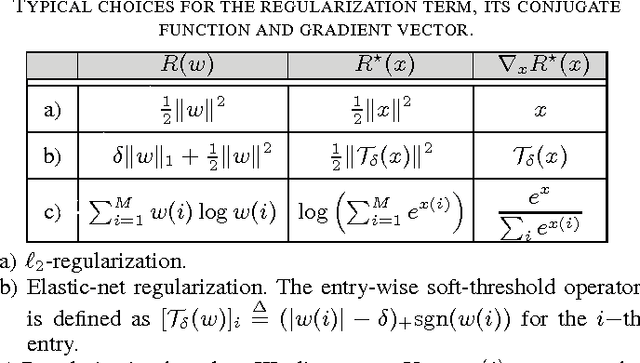
The stochastic dual coordinate-ascent (S-DCA) technique is a useful alternative to the traditional stochastic gradient-descent algorithm for solving large-scale optimization problems due to its scalability to large data sets and strong theoretical guarantees. However, the available S-DCA formulation is limited to finite sample sizes and relies on performing multiple passes over the same data. This formulation is not well-suited for online implementations where data keep streaming in. In this work, we develop an {\em online} dual coordinate-ascent (O-DCA) algorithm that is able to respond to streaming data and does not need to revisit the past data. This feature embeds the resulting construction with continuous adaptation, learning, and tracking abilities, which are particularly attractive for online learning scenarios.

Information Exchange and Learning Dynamics over Weakly-Connected Adaptive Networks

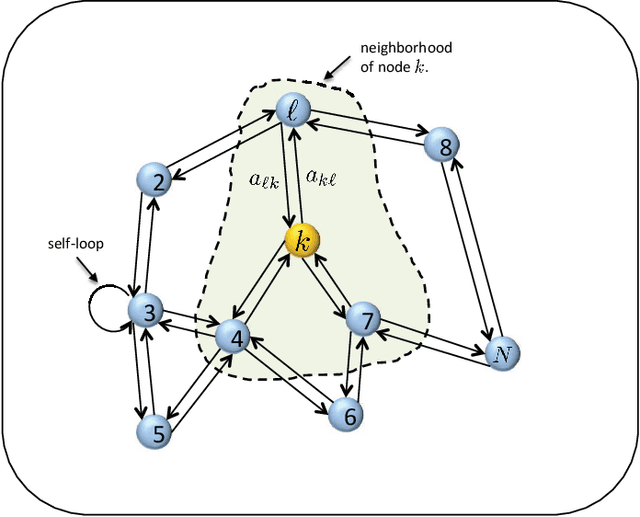
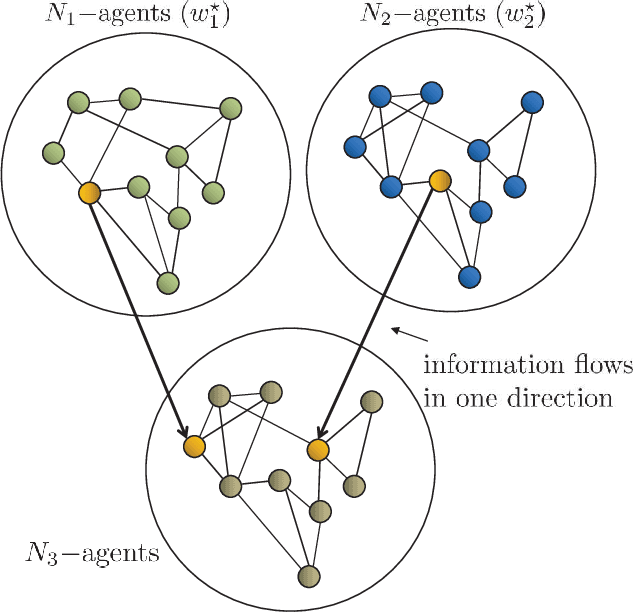
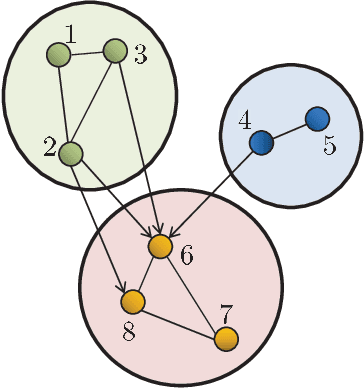
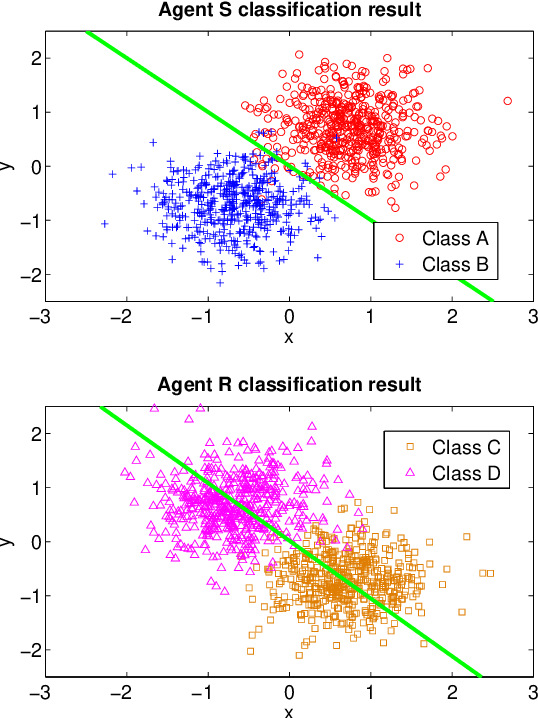
The paper examines the learning mechanism of adaptive agents over weakly-connected graphs and reveals an interesting behavior on how information flows through such topologies. The results clarify how asymmetries in the exchange of data can mask local information at certain agents and make them totally dependent on other agents. A leader-follower relationship develops with the performance of some agents being fully determined by the performance of other agents that are outside their domain of influence. This scenario can arise, for example, due to intruder attacks by malicious agents or as the result of failures by some critical links. The findings in this work help explain why strong-connectivity of the network topology, adaptation of the combination weights, and clustering of agents are important ingredients to equalize the learning abilities of all agents against such disturbances. The results also clarify how weak-connectivity can be helpful in reducing the effect of outlier data on learning performance.

Stability and Performance Limits of Adaptive Primal-Dual Networks

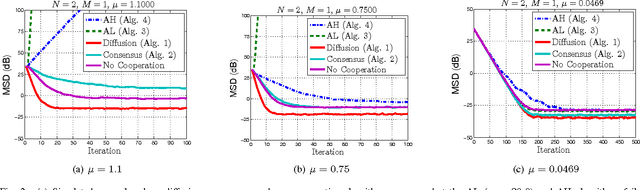
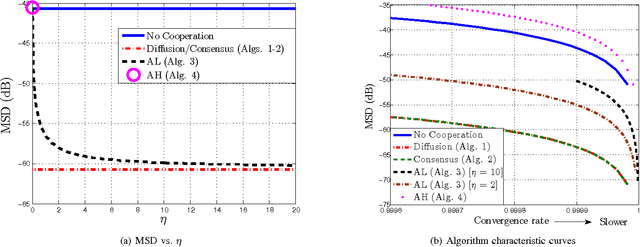
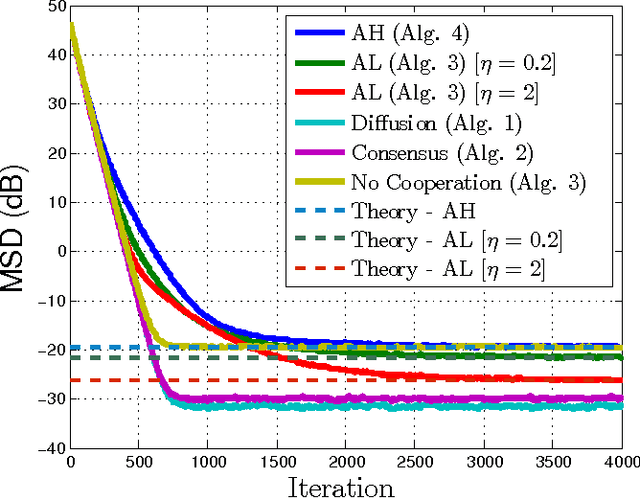
This work studies distributed primal-dual strategies for adaptation and learning over networks from streaming data. Two first-order methods are considered based on the Arrow-Hurwicz (AH) and augmented Lagrangian (AL) techniques. Several revealing results are discovered in relation to the performance and stability of these strategies when employed over adaptive networks. The conclusions establish that the advantages that these methods have for deterministic optimization problems do not necessarily carry over to stochastic optimization problems. It is found that they have narrower stability ranges and worse steady-state mean-square-error performance than primal methods of the consensus and diffusion type. It is also found that the AH technique can become unstable under a partial observation model, while the other techniques are able to recover the unknown under this scenario. A method to enhance the performance of AL strategies is proposed by tying the selection of the step-size to their regularization parameter. It is shown that this method allows the AL algorithm to approach the performance of consensus and diffusion strategies but that it remains less stable than these other strategies.

Asynchronous Adaptation and Learning over Networks - Part III: Comparison Analysis

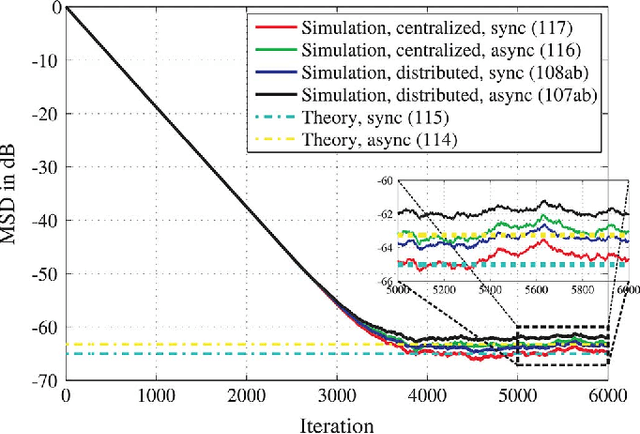
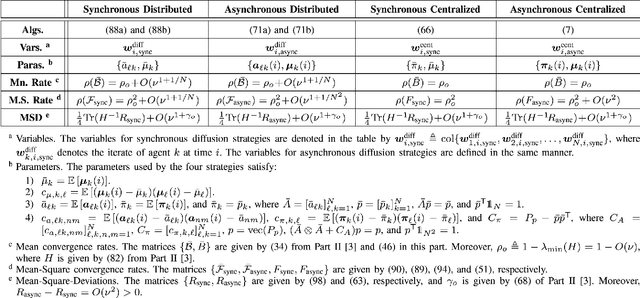
In Part II [3] we carried out a detailed mean-square-error analysis of the performance of asynchronous adaptation and learning over networks under a fairly general model for asynchronous events including random topologies, random link failures, random data arrival times, and agents turning on and off randomly. In this Part III, we compare the performance of synchronous and asynchronous networks. We also compare the performance of decentralized adaptation against centralized stochastic-gradient (batch) solutions. Two interesting conclusions stand out. First, the results establish that the performance of adaptive networks is largely immune to the effect of asynchronous events: the mean and mean-square convergence rates and the asymptotic bias values are not degraded relative to synchronous or centralized implementations. Only the steady-state mean-square-deviation suffers a degradation in the order of $\nu$, which represents the small step-size parameters used for adaptation. Second, the results show that the adaptive distributed network matches the performance of the centralized solution. These conclusions highlight another critical benefit of cooperation by networked agents: cooperation does not only enhance performance in comparison to stand-alone single-agent processing, but it also endows the network with remarkable resilience to various forms of random failure events and is able to deliver performance that is as powerful as batch solutions.