Ali H. Sayed
On the Arithmetic and Geometric Fusion of Beliefs for Distributed Inference
Apr 28, 2022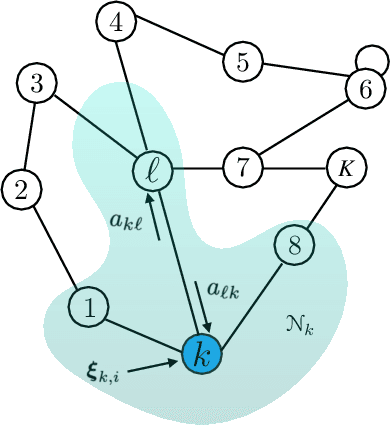
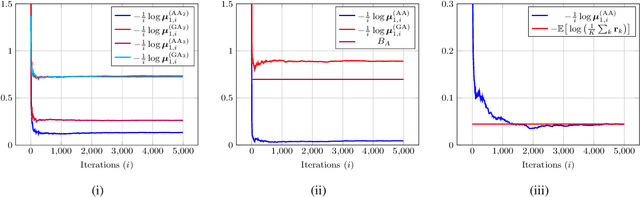
Abstract:We study the asymptotic learning rates under linear and log-linear combination rules of belief vectors in a distributed hypothesis testing problem. We show that under both combination strategies, agents are able to learn the truth exponentially fast, with a faster rate under log-linear fusion. We examine the gap between the rates in terms of network connectivity and information diversity. We also provide closed-form expressions for special cases involving federated architectures and exchangeable networks.
Dencentralized learning in the presence of low-rank noise
Mar 18, 2022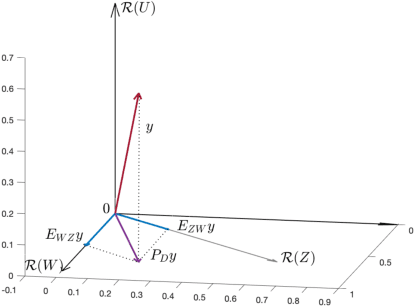
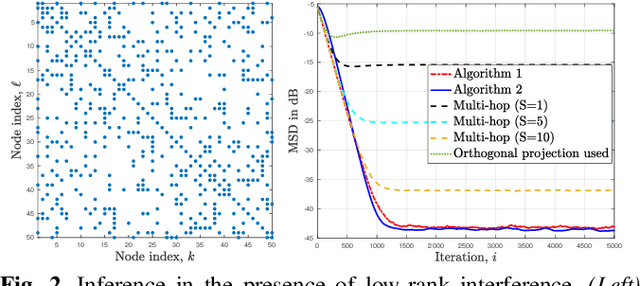
Abstract:Observations collected by agents in a network may be unreliable due to observation noise or interference. This paper proposes a distributed algorithm that allows each node to improve the reliability of its own observation by relying solely on local computations and interactions with immediate neighbors, assuming that the field (graph signal) monitored by the network lies in a low-dimensional subspace and that a low-rank noise is present in addition to the usual full-rank noise. While oblique projections can be used to project measurements onto a low-rank subspace along a direction that is oblique to the subspace, the resulting solution is not distributed. Starting from the centralized solution, we propose an algorithm that performs the oblique projection of the overall set of observations onto the signal subspace in an iterative and distributed manner. We then show how the oblique projection framework can be extended to handle distributed learning and adaptation problems over networks.
Explainability and Graph Learning from Social Interactions
Mar 14, 2022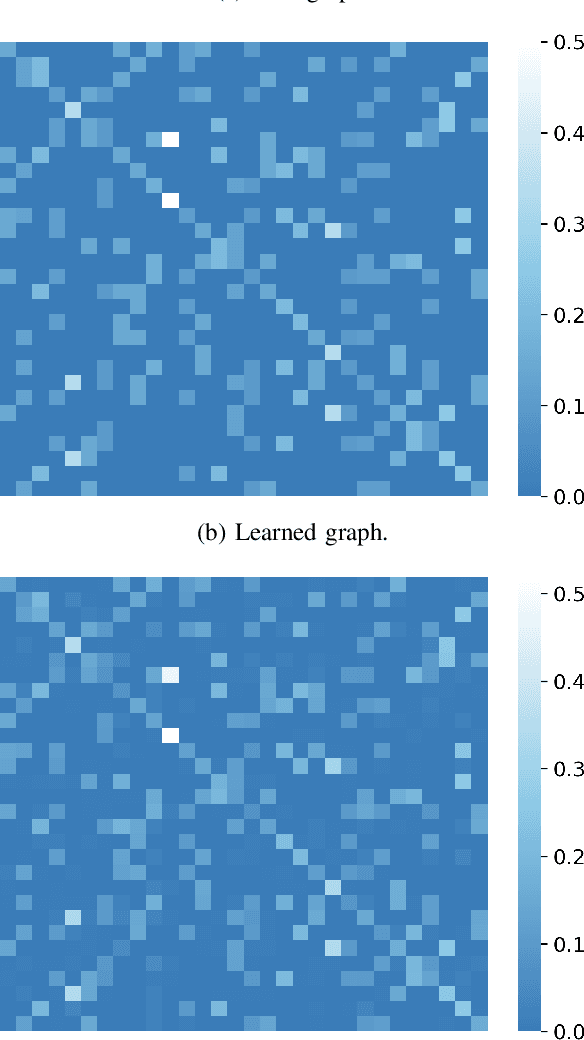
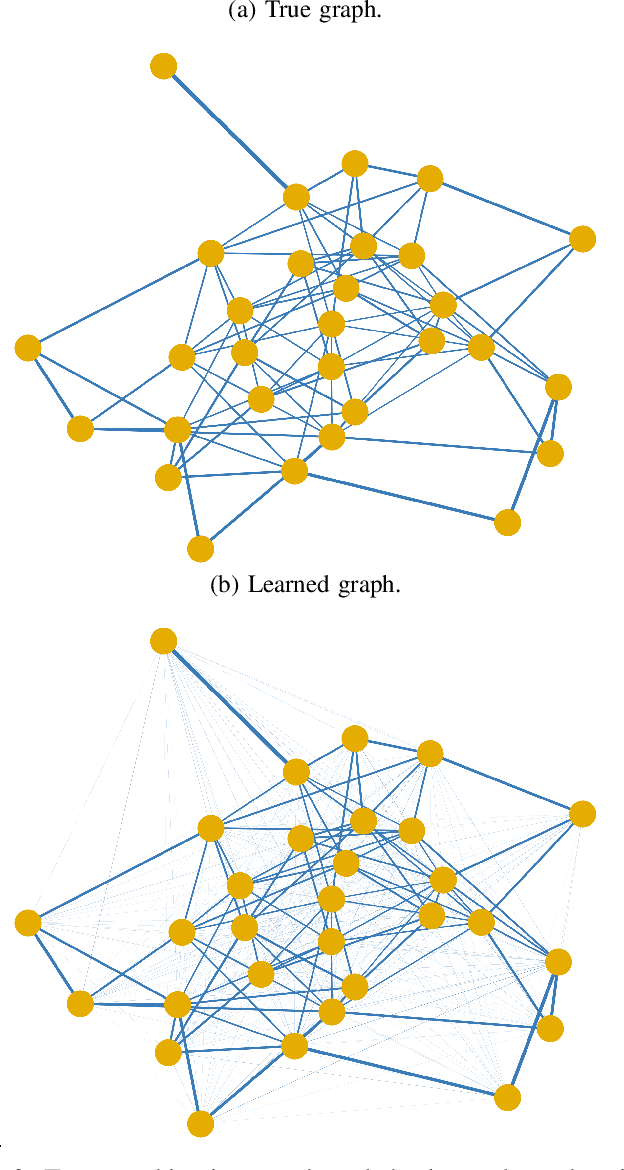
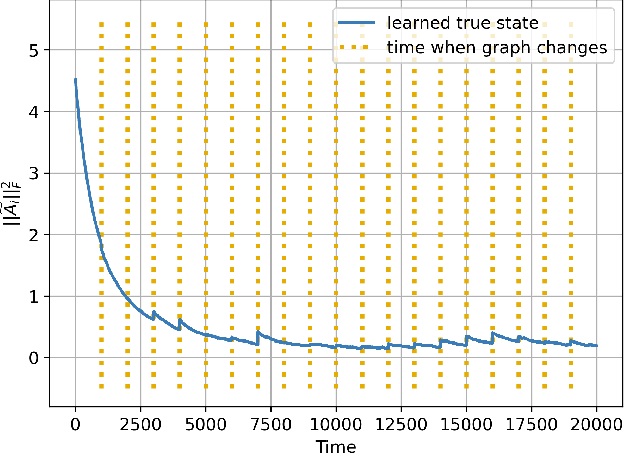
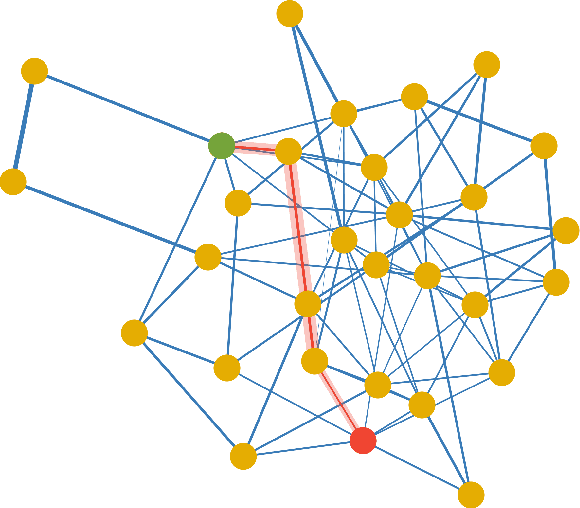
Abstract:Social learning algorithms provide models for the formation of opinions over social networks resulting from local reasoning and peer-to-peer exchanges. Interactions occur over an underlying graph topology, which describes the flow of information among the agents. In this work, we propose a technique that addresses questions of explainability and interpretability when the graph is hidden. Given observations of the evolution of the belief over time, we aim to infer the underlying graph topology, discover pairwise influences between the agents, and identify significant trajectories in the network. The proposed framework is online in nature and can adapt dynamically to changes in the graph topology or the true hypothesis.
Privatized Graph Federated Learning
Mar 14, 2022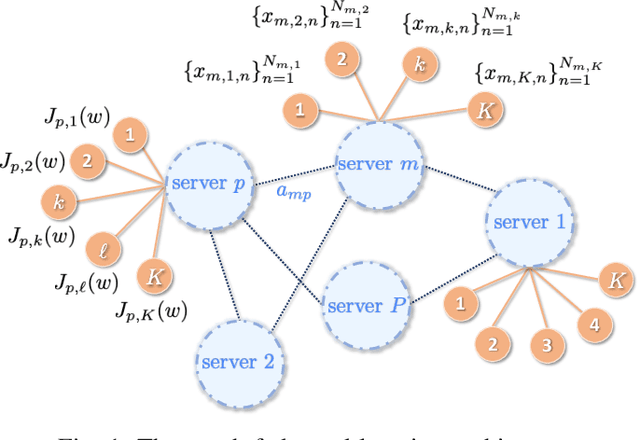
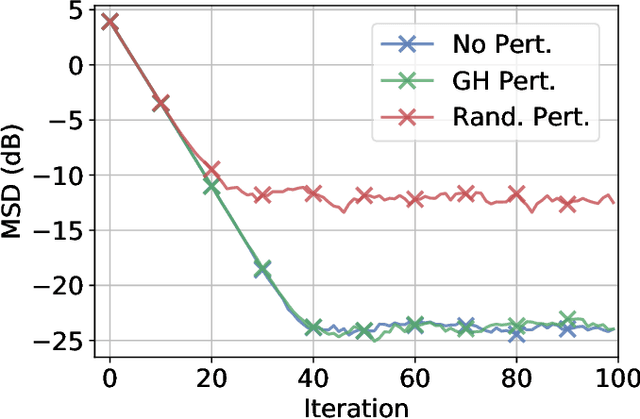
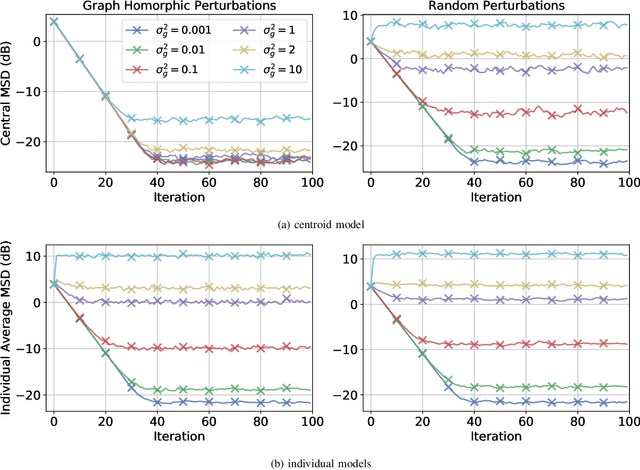
Abstract:Federated learning is a semi-distributed algorithm, where a server communicates with multiple dispersed clients to learn a global model. The federated architecture is not robust and is sensitive to communication and computational overloads due to its one-master multi-client structure. It can also be subject to privacy attacks targeting personal information on the communication links. In this work, we introduce graph federated learning (GFL), which consists of multiple federated units connected by a graph. We then show how graph homomorphic perturbations can be used to ensure the algorithm is differentially private. We conduct both convergence and privacy theoretical analyses and illustrate performance by means of computer simulations.
Optimal Aggregation Strategies for Social Learning over Graphs
Mar 14, 2022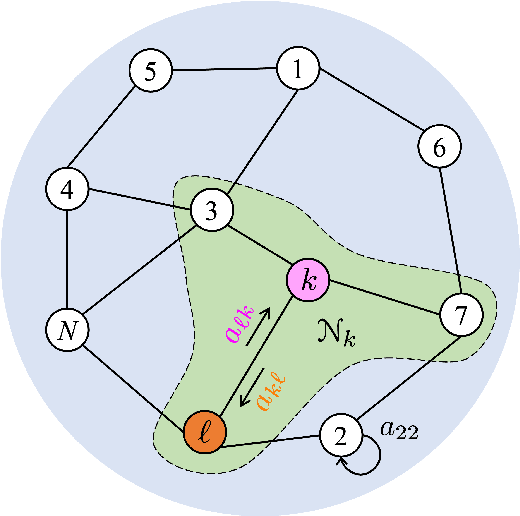
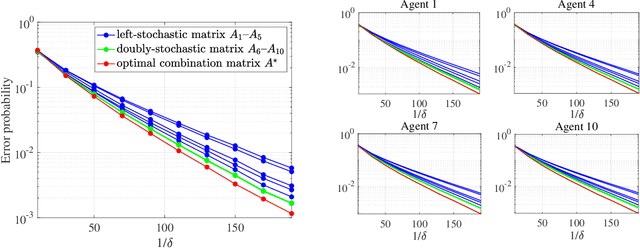
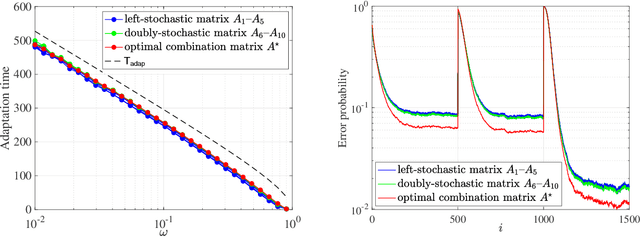
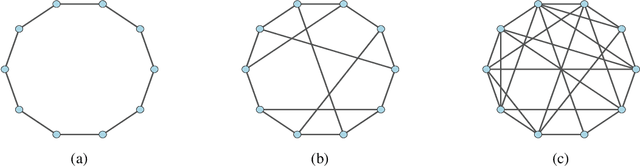
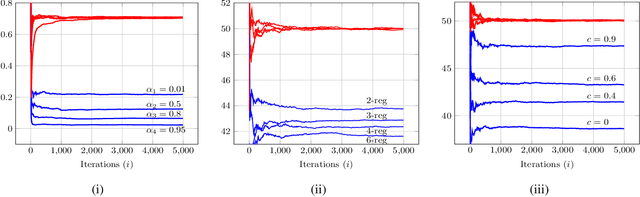
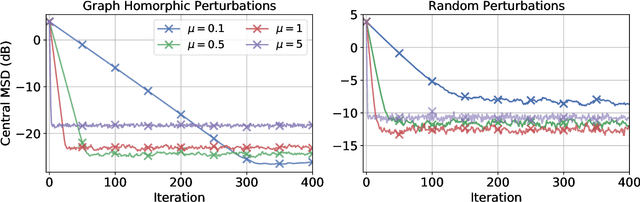
Abstract:Adaptive social learning is a useful tool for studying distributed decision-making problems over graphs. This paper investigates the effect of combination policies on the performance of adaptive social learning strategies. Using large-deviation analysis, it first derives a bound on the probability of error and characterizes the optimal selection for the Perron eigenvectors of the combination policies. It subsequently studies the effect of the combination policy on the transient behavior of the learning strategy by estimating the adaptation time in the small signal-to-noise ratio regime. In the process, it is discovered that, interestingly, the influence of the combination policy on the transient behavior is insignificant, and thus it is more critical to employ policies that enhance the steady-state performance. The theoretical conclusions are illustrated by means of computer simulations.
Online Graph Learning from Social Interactions
Mar 11, 2022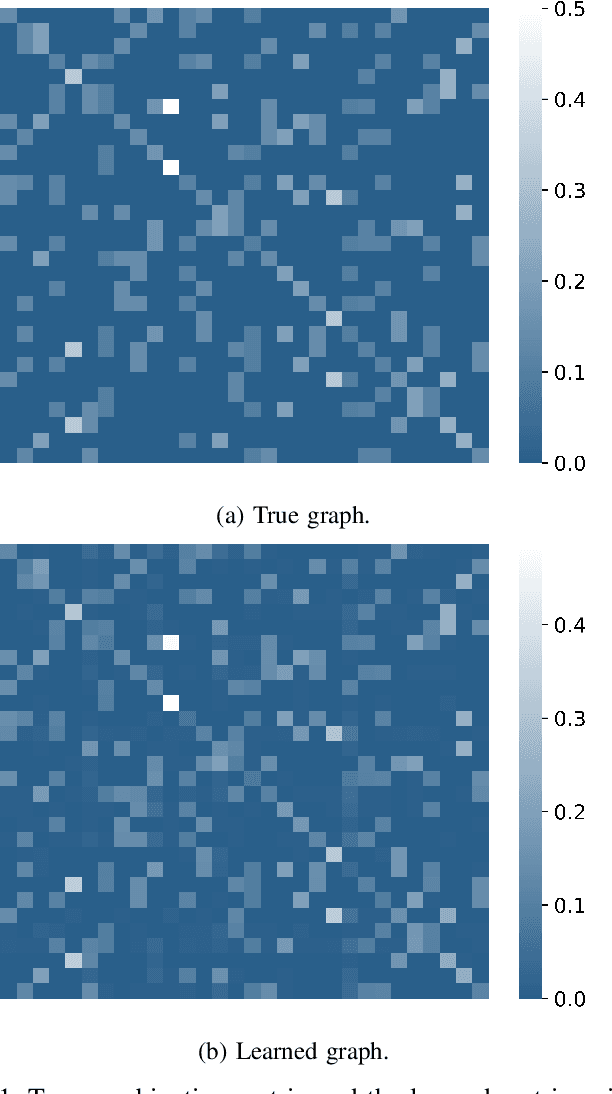
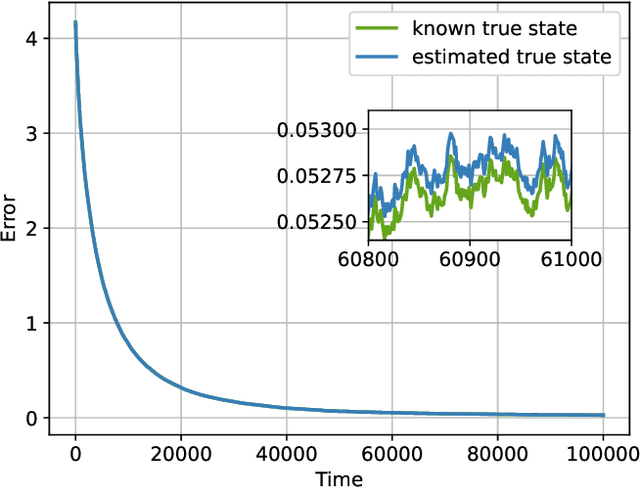
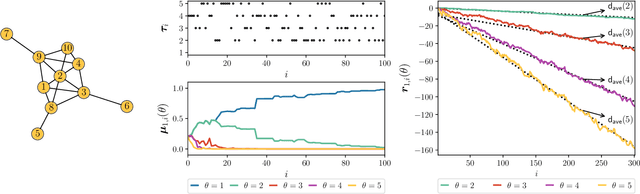
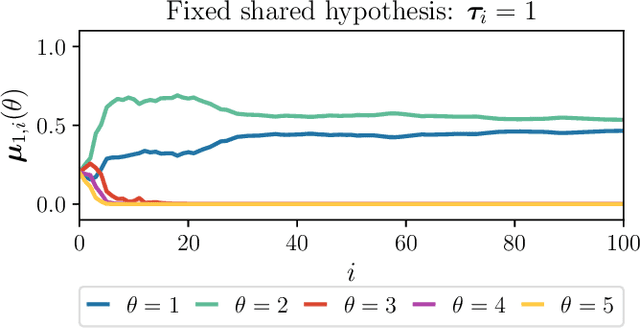
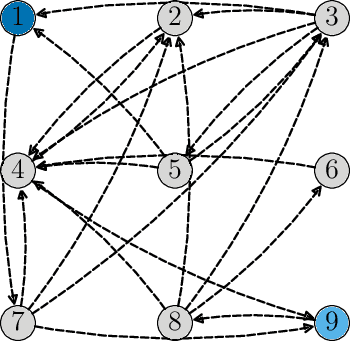
Abstract:Social learning algorithms provide models for the formation of opinions over social networks resulting from local reasoning and peer-to-peer exchanges. Interactions occur over an underlying graph topology, which describes the flow of information and relative influence between pairs of agents. For a given graph topology, these algorithms allow for the prediction of formed opinions. In this work, we study the inverse problem. Given a social learning model and observations of the evolution of beliefs over time, we aim at identifying the underlying graph topology. The learned graph allows for the inference of pairwise influence between agents, the overall influence agents have over the behavior of the network, as well as the flow of information through the social network. The proposed algorithm is online in nature and can adapt dynamically to changes in the graph topology or the true hypothesis.
Random Information Sharing over Social Networks
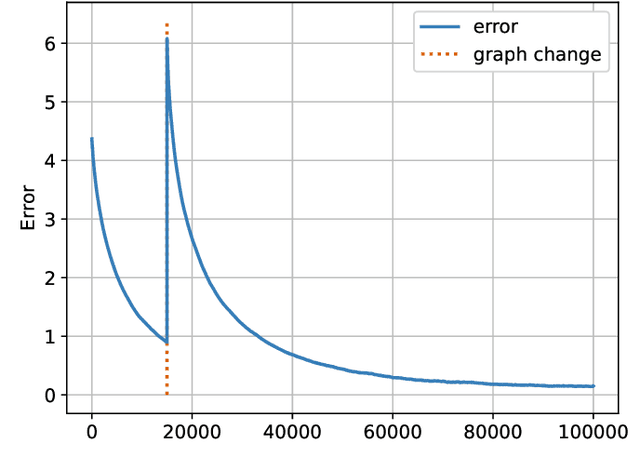
Mar 04, 2022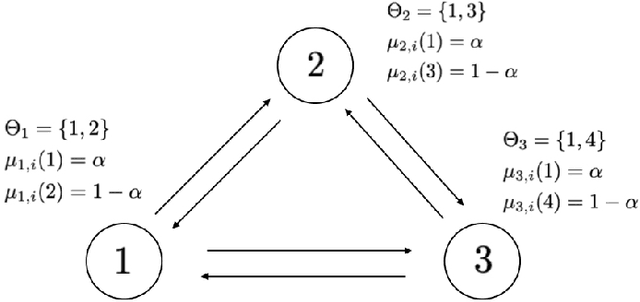

Abstract:This work studies the learning process over social networks under partial and random information sharing. In traditional social learning, agents exchange full information with each other while trying to infer the true state of nature. We study the case where agents share information about only one hypothesis, i.e., the trending topic, which can be randomly changing at every iteration. We show that agents can learn the true hypothesis even if they do not discuss it, at rates comparable to traditional social learning. We also show that using one's own belief as a prior for estimating the neighbors' non-transmitted components might create opinion clusters that prevent learning with full confidence. This practice however avoids the complete rejection of the truth.
Social Learning under Randomized Collaborations
Jan 26, 2022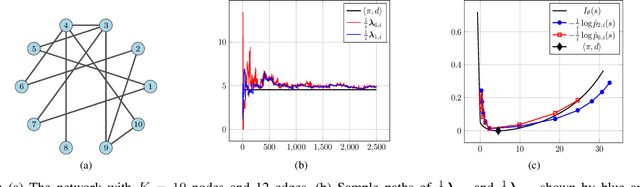
Abstract:We study a social learning scheme where at every time instant, each agent chooses to receive information from one of its neighbors at random. We show that under this sparser communication scheme, the agents learn the truth eventually and the asymptotic convergence rate remains the same as the standard algorithms which use more communication resources. We also derive large deviation estimates of the log-belief ratios for a special case where each agent replaces its belief with that of the chosen neighbor.
Combinations of Adaptive Filters
Dec 22, 2021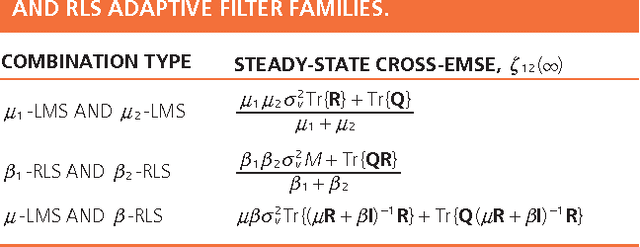

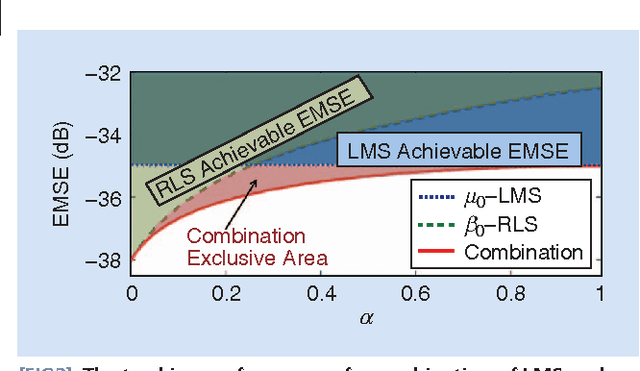
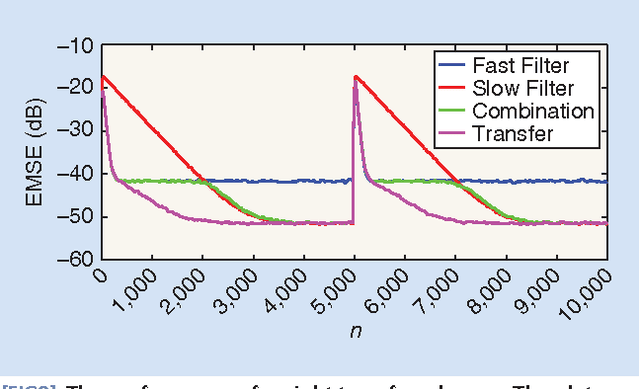
Abstract:Adaptive filters are at the core of many signal processing applications, ranging from acoustic noise supression to echo cancelation, array beamforming, channel equalization, to more recent sensor network applications in surveillance, target localization, and tracking. A trending approach in this direction is to recur to in-network distributed processing in which individual nodes implement adaptation rules and diffuse their estimation to the network. When the a priori knowledge about the filtering scenario is limited or imprecise, selecting the most adequate filter structure and adjusting its parameters becomes a challenging task, and erroneous choices can lead to inadequate performance. To address this difficulty, one useful approach is to rely on combinations of adaptive structures. The combination of adaptive filters exploits to some extent the same divide and conquer principle that has also been successfully exploited by the machine-learning community (e.g., in bagging or boosting). In particular, the problem of combining the outputs of several learning algorithms (mixture of experts) has been studied in the computational learning field under a different perspective: rather than studying the expected performance of the mixture, deterministic bounds are derived that apply to individual sequences and, therefore, reflect worst-case scenarios. These bounds require assumptions different from the ones typically used in adaptive filtering, which is the emphasis of this overview article. We review the key ideas and principles behind these combination schemes, with emphasis on design rules. We also illustrate their performance with a variety of examples.
Learning from Heterogeneous Data Based on Social Interactions over Graphs
Dec 17, 2021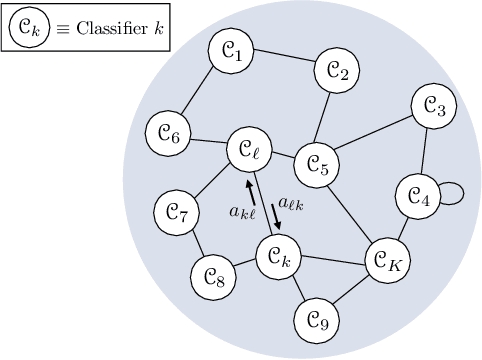
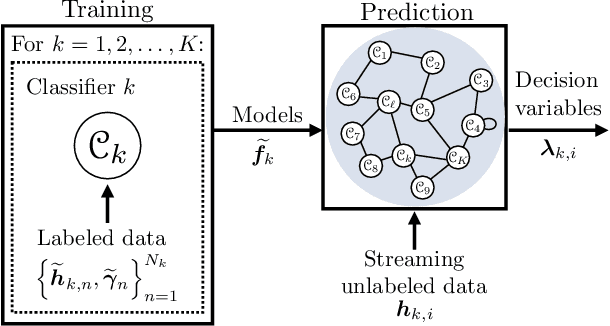
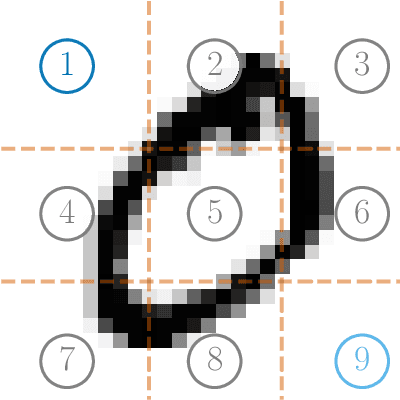
Abstract:This work proposes a decentralized architecture, where individual agents aim at solving a classification problem while observing streaming features of different dimensions and arising from possibly different distributions. In the context of social learning, several useful strategies have been developed, which solve decision making problems through local cooperation across distributed agents and allow them to learn from streaming data. However, traditional social learning strategies rely on the fundamental assumption that each agent has significant prior knowledge of the underlying distribution of the observations. In this work we overcome this issue by introducing a machine learning framework that exploits social interactions over a graph, leading to a fully data-driven solution to the distributed classification problem. In the proposed social machine learning (SML) strategy, two phases are present: in the training phase, classifiers are independently trained to generate a belief over a set of hypotheses using a finite number of training samples; in the prediction phase, classifiers evaluate streaming unlabeled observations and share their instantaneous beliefs with neighboring classifiers. We show that the SML strategy enables the agents to learn consistently under this highly-heterogeneous setting and allows the network to continue learning even during the prediction phase when it is deciding on unlabeled samples. The prediction decisions are used to continually improve performance thereafter in a manner that is markedly different from most existing static classification schemes where, following training, the decisions on unlabeled data are not re-used to improve future performance.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge