Signal from Structure: Exploiting Submodular Upper Bounds in Generative Flow Networks

Generative Flow Networks (GFlowNets; GFNs) are a class of generative models that learn to sample compositional objects proportionally to their a priori unknown value, their reward. We focus on the case where the reward has a specified, actionable structure, namely that it is submodular. We show submodularity can be harnessed to retrieve upper bounds on the reward of compositional objects that have not yet been observed. We provide in-depth analyses of the probability of such bounds occurring, as well as how many unobserved compositional objects can be covered by a bound. Following the Optimism in the Face of Uncertainty principle, we then introduce SUBo-GFN, which uses the submodular upper bounds to train a GFN. We show that SUBo-GFN generates orders of magnitude more training data than classical GFNs for the same number of queries to the reward function. We demonstrate the effectiveness of SUBo-GFN in terms of distribution matching and high-quality candidate generation on synthetic and real-world submodular tasks.

Neural Bandits for Data Mining: Searching for Dangerous Polypharmacy

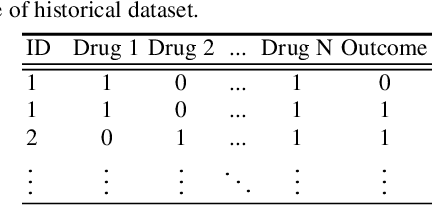
Polypharmacy, most often defined as the simultaneous consumption of five or more drugs at once, is a prevalent phenomenon in the older population. Some of these polypharmacies, deemed inappropriate, may be associated with adverse health outcomes such as death or hospitalization. Considering the combinatorial nature of the problem as well as the size of claims database and the cost to compute an exact association measure for a given drug combination, it is impossible to investigate every possible combination of drugs. Therefore, we propose to optimize the search for potentially inappropriate polypharmacies (PIPs). To this end, we propose the OptimNeuralTS strategy, based on Neural Thompson Sampling and differential evolution, to efficiently mine claims datasets and build a predictive model of the association between drug combinations and health outcomes. We benchmark our method using two datasets generated by an internally developed simulator of polypharmacy data containing 500 drugs and 100 000 distinct combinations. Empirically, our method can detect up to 33\% of PIPs while maintaining an average precision score of 99\% using 10 000 time steps.