Fast and Credible Likelihood-Free Cosmology with Truncated Marginal Neural Ratio Estimation

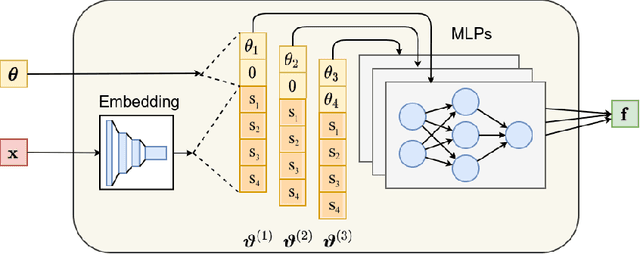
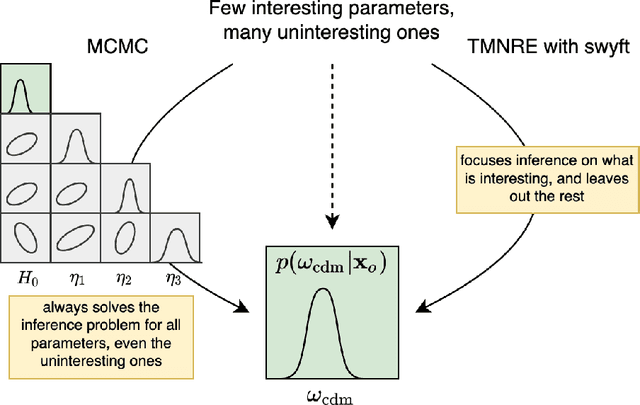
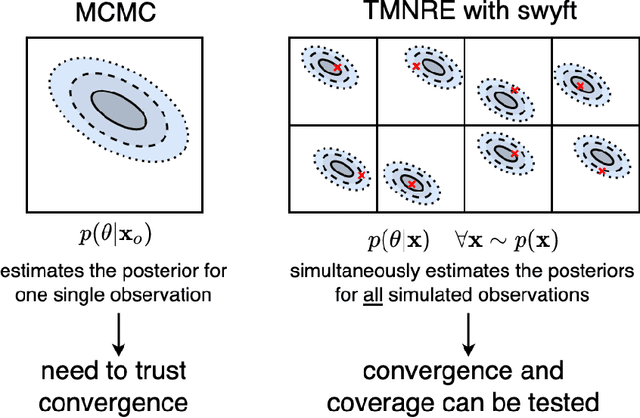
Sampling-based inference techniques are central to modern cosmological data analysis; these methods, however, scale poorly with dimensionality and typically require approximate or intractable likelihoods. In this paper we describe how Truncated Marginal Neural Ratio Estimation (TMNRE) (a new approach in so-called simulation-based inference) naturally evades these issues, improving the $(i)$ efficiency, $(ii)$ scalability, and $(iii)$ trustworthiness of the inferred posteriors. Using measurements of the Cosmic Microwave Background (CMB), we show that TMNRE can achieve converged posteriors using orders of magnitude fewer simulator calls than conventional Markov Chain Monte Carlo (MCMC) methods. Remarkably, the required number of samples is effectively independent of the number of nuisance parameters. In addition, a property called \emph{local amortization} allows the performance of rigorous statistical consistency checks that are not accessible to sampling-based methods. TMNRE promises to become a powerful tool for cosmological data analysis, particularly in the context of extended cosmologies, where the timescale required for conventional sampling-based inference methods to converge can greatly exceed that of simple cosmological models such as $\Lambda$CDM. To perform these computations, we use an implementation of TMNRE via the open-source code \texttt{swyft}.

Truncated Marginal Neural Ratio Estimation

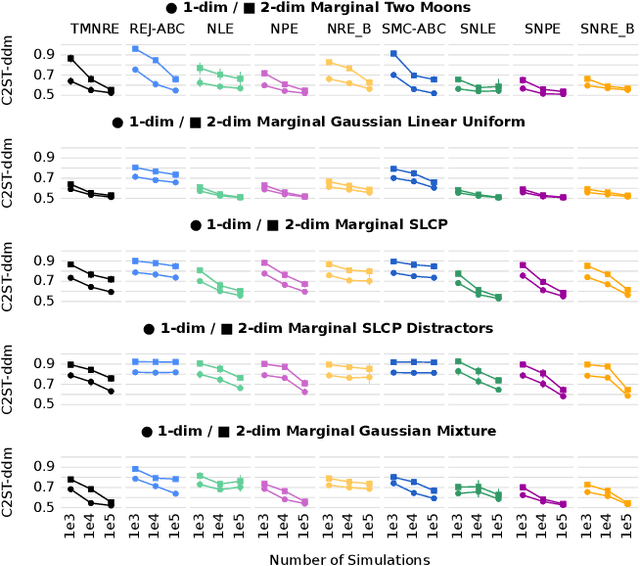
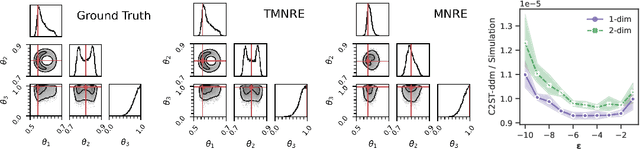
Parametric stochastic simulators are ubiquitous in science, often featuring high-dimensional input parameters and/or an intractable likelihood. Performing Bayesian parameter inference in this context can be challenging. We present a neural simulator-based inference algorithm which simultaneously offers simulation efficiency and fast empirical posterior testability, which is unique among modern algorithms. Our approach is simulation efficient by simultaneously estimating low-dimensional marginal posteriors instead of the joint posterior and by proposing simulations targeted to an observation of interest via a prior suitably truncated by an indicator function. Furthermore, by estimating a locally amortized posterior our algorithm enables efficient empirical tests of the robustness of the inference results. Such tests are important for sanity-checking inference in real-world applications, which do not feature a known ground truth. We perform experiments on a marginalized version of the simulation-based inference benchmark and two complex and narrow posteriors, highlighting the simulator efficiency of our algorithm as well as the quality of the estimated marginal posteriors. Implementation on GitHub.

Topological Echoes of Primordial Physics in the Universe at Large Scales

We present a pipeline for characterizing and constraining initial conditions in cosmology via persistent homology. The cosmological observable of interest is the cosmic web of large scale structure, and the initial conditions in question are non-Gaussianities (NG) of primordial density perturbations. We compute persistence diagrams and derived statistics for simulations of dark matter halos with Gaussian and non-Gaussian initial conditions. For computational reasons and to make contact with experimental observations, our pipeline computes persistence in sub-boxes of full simulations and simulations are subsampled to uniform halo number. We use simulations with large NG ($f_{\rm NL}^{\rm loc}=250$) as templates for identifying data with mild NG ($f_{\rm NL}^{\rm loc}=10$), and running the pipeline on several cubic volumes of size $40~(\textrm{Gpc/h})^{3}$, we detect $f_{\rm NL}^{\rm loc}=10$ at $97.5\%$ confidence on $\sim 85\%$ of the volumes for our best single statistic. Throughout we benefit from the interpretability of topological features as input for statistical inference, which allows us to make contact with previous first-principles calculations and make new predictions.

Interpretable Phase Detection and Classification with Persistent Homology

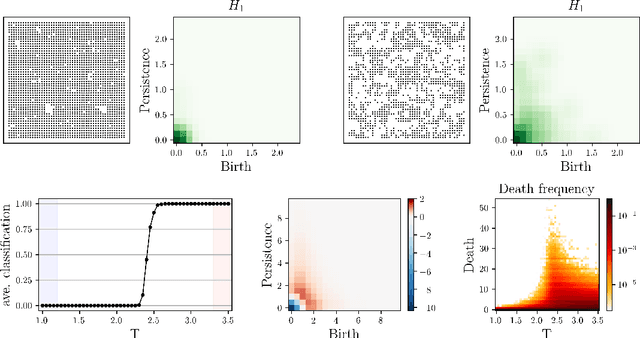
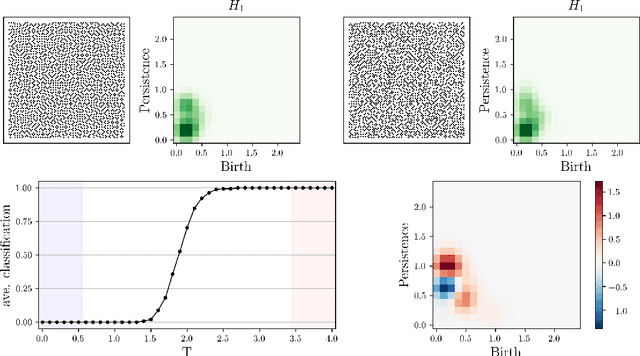
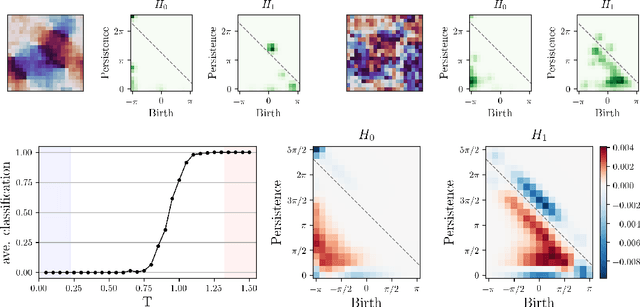
We apply persistent homology to the task of discovering and characterizing phase transitions, using lattice spin models from statistical physics for working examples. Persistence images provide a useful representation of the homological data for conducting statistical tasks. To identify the phase transitions, a simple logistic regression on these images is sufficient for the models we consider, and interpretable order parameters are then read from the weights of the regression. Magnetization, frustration and vortex-antivortex structure are identified as relevant features for characterizing phase transitions.

Simulation-efficient marginal posterior estimation with swyft: stop wasting your precious time

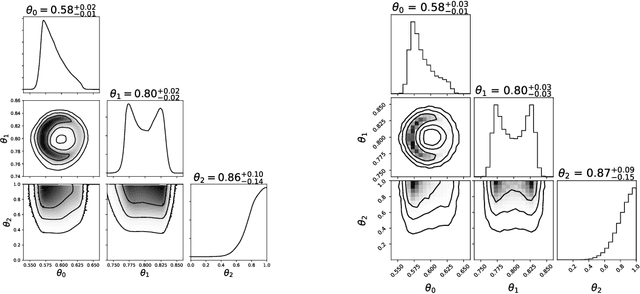
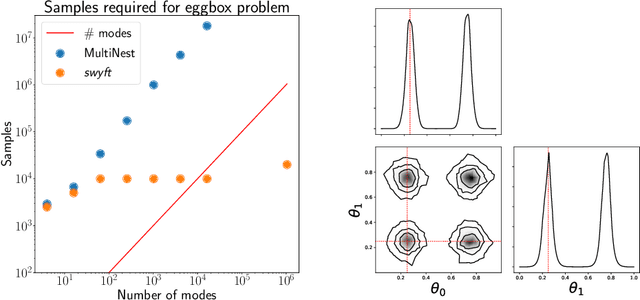
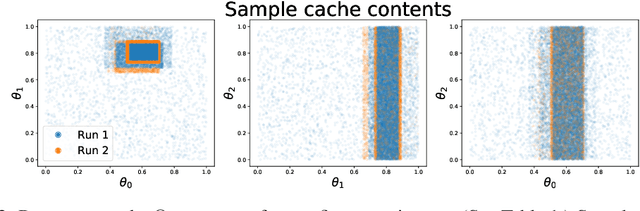
We present algorithms (a) for nested neural likelihood-to-evidence ratio estimation, and (b) for simulation reuse via an inhomogeneous Poisson point process cache of parameters and corresponding simulations. Together, these algorithms enable automatic and extremely simulator efficient estimation of marginal and joint posteriors. The algorithms are applicable to a wide range of physics and astronomy problems and typically offer an order of magnitude better simulator efficiency than traditional likelihood-based sampling methods. Our approach is an example of likelihood-free inference, thus it is also applicable to simulators which do not offer a tractable likelihood function. Simulator runs are never rejected and can be automatically reused in future analysis. As functional prototype implementation we provide the open-source software package swyft.

Searching the Landscape of Flux Vacua with Genetic Algorithms

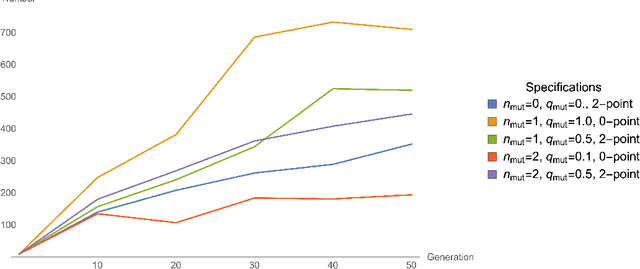
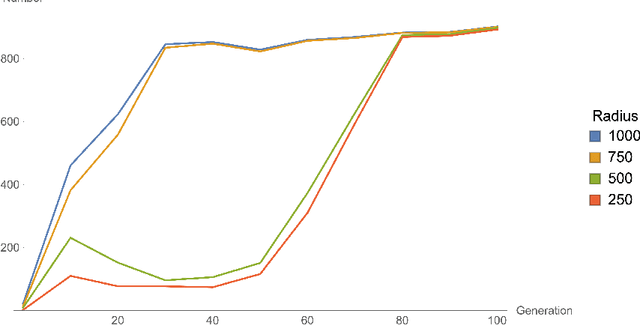
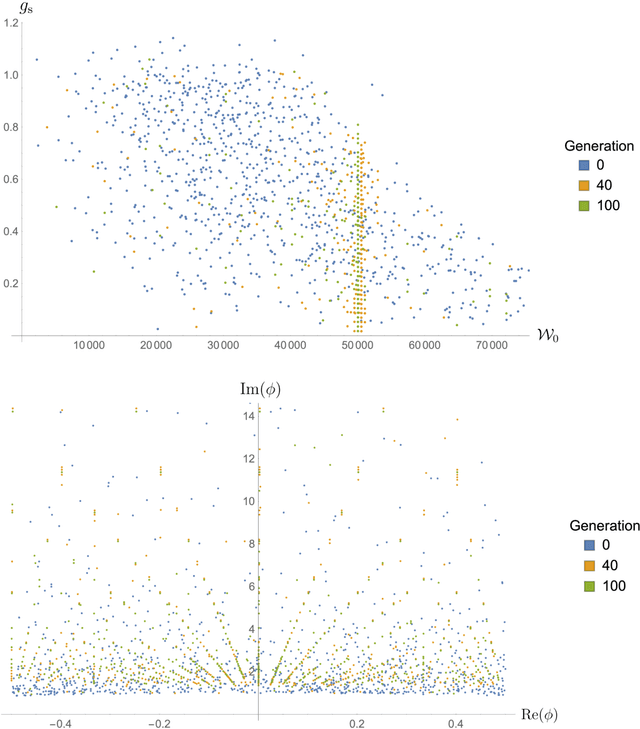
In this paper, we employ genetic algorithms to explore the landscape of type IIB flux vacua. We show that genetic algorithms can efficiently scan the landscape for viable solutions satisfying various criteria. More specifically, we consider a symmetric $T^{6}$ as well as the conifold region of a Calabi-Yau hypersurface. We argue that in both cases genetic algorithms are powerful tools for finding flux vacua with interesting phenomenological properties. We also compare genetic algorithms to algorithms based on different breeding mechanisms as well as random walk approaches.