$ρ$-Diffusion: A diffusion-based density estimation framework for computational physics

In physics, density $\rho(\cdot)$ is a fundamentally important scalar function to model, since it describes a scalar field or a probability density function that governs a physical process. Modeling $\rho(\cdot)$ typically scales poorly with parameter space, however, and quickly becomes prohibitively difficult and computationally expensive. One promising avenue to bypass this is to leverage the capabilities of denoising diffusion models often used in high-fidelity image generation to parameterize $\rho(\cdot)$ from existing scientific data, from which new samples can be trivially sampled from. In this paper, we propose $\rho$-Diffusion, an implementation of denoising diffusion probabilistic models for multidimensional density estimation in physics, which is currently in active development and, from our results, performs well on physically motivated 2D and 3D density functions. Moreover, we propose a novel hashing technique that allows $\rho$-Diffusion to be conditioned by arbitrary amounts of physical parameters of interest.

A hybrid approach for solving the gravitational N-body problem with Artificial Neural Networks

Simulating the evolution of the gravitational N-body problem becomes extremely computationally expensive as N increases since the problem complexity scales quadratically with the number of bodies. We study the use of Artificial Neural Networks (ANNs) to replace expensive parts of the integration of planetary systems. Neural networks that include physical knowledge have grown in popularity in the last few years, although few attempts have been made to use them to speed up the simulation of the motion of celestial bodies. We study the advantages and limitations of using Hamiltonian Neural Networks to replace computationally expensive parts of the numerical simulation. We compare the results of the numerical integration of a planetary system with asteroids with those obtained by a Hamiltonian Neural Network and a conventional Deep Neural Network, with special attention to understanding the challenges of this problem. Due to the non-linear nature of the gravitational equations of motion, errors in the integration propagate. To increase the robustness of a method that uses neural networks, we propose a hybrid integrator that evaluates the prediction of the network and replaces it with the numerical solution if considered inaccurate. Hamiltonian Neural Networks can make predictions that resemble the behavior of symplectic integrators but are challenging to train and in our case fail when the inputs differ ~7 orders of magnitude. In contrast, Deep Neural Networks are easy to train but fail to conserve energy, leading to fast divergence from the reference solution. The hybrid integrator designed to include the neural networks increases the reliability of the method and prevents large energy errors without increasing the computing cost significantly. For this problem, the use of neural networks results in faster simulations when the number of asteroids is >70.

Neural Symplectic Integrator with Hamiltonian Inductive Bias for the Gravitational $N$-body Problem

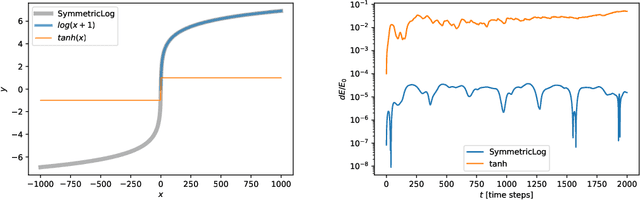
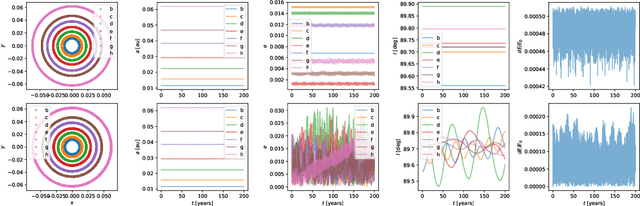
The gravitational $N$-body problem, which is fundamentally important in astrophysics to predict the motion of $N$ celestial bodies under the mutual gravity of each other, is usually solved numerically because there is no known general analytical solution for $N>2$. Can an $N$-body problem be solved accurately by a neural network (NN)? Can a NN observe long-term conservation of energy and orbital angular momentum? Inspired by Wistom & Holman (1991)'s symplectic map, we present a neural $N$-body integrator for splitting the Hamiltonian into a two-body part, solvable analytically, and an interaction part that we approximate with a NN. Our neural symplectic $N$-body code integrates a general three-body system for $10^{5}$ steps without diverting from the ground truth dynamics obtained from a traditional $N$-body integrator. Moreover, it exhibits good inductive bias by successfully predicting the evolution of $N$-body systems that are no part of the training set.

Fast and Credible Likelihood-Free Cosmology with Truncated Marginal Neural Ratio Estimation

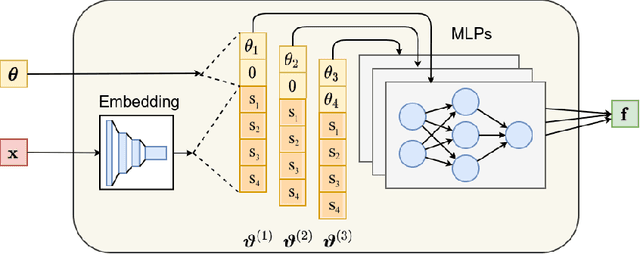
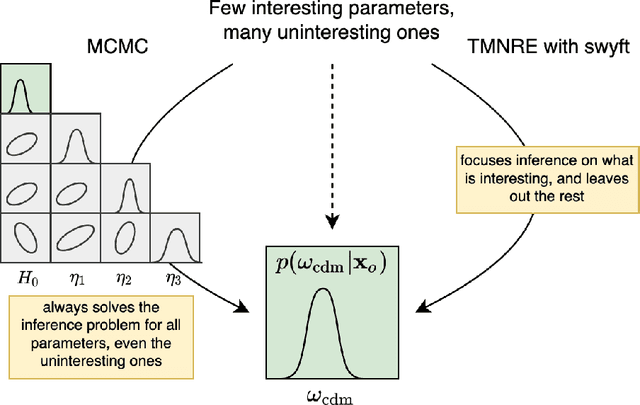
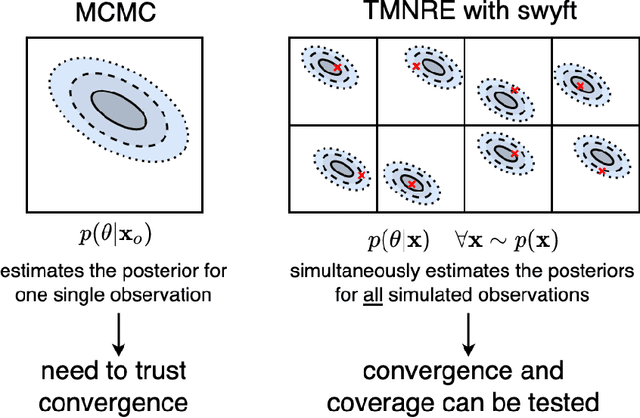
Sampling-based inference techniques are central to modern cosmological data analysis; these methods, however, scale poorly with dimensionality and typically require approximate or intractable likelihoods. In this paper we describe how Truncated Marginal Neural Ratio Estimation (TMNRE) (a new approach in so-called simulation-based inference) naturally evades these issues, improving the $(i)$ efficiency, $(ii)$ scalability, and $(iii)$ trustworthiness of the inferred posteriors. Using measurements of the Cosmic Microwave Background (CMB), we show that TMNRE can achieve converged posteriors using orders of magnitude fewer simulator calls than conventional Markov Chain Monte Carlo (MCMC) methods. Remarkably, the required number of samples is effectively independent of the number of nuisance parameters. In addition, a property called \emph{local amortization} allows the performance of rigorous statistical consistency checks that are not accessible to sampling-based methods. TMNRE promises to become a powerful tool for cosmological data analysis, particularly in the context of extended cosmologies, where the timescale required for conventional sampling-based inference methods to converge can greatly exceed that of simple cosmological models such as $\Lambda$CDM. To perform these computations, we use an implementation of TMNRE via the open-source code \texttt{swyft}.