OpenAI GPT-5 System Card

This is the system card published alongside the OpenAI GPT-5 launch, August 2025. GPT-5 is a unified system with a smart and fast model that answers most questions, a deeper reasoning model for harder problems, and a real-time router that quickly decides which model to use based on conversation type, complexity, tool needs, and explicit intent (for example, if you say 'think hard about this' in the prompt). The router is continuously trained on real signals, including when users switch models, preference rates for responses, and measured correctness, improving over time. Once usage limits are reached, a mini version of each model handles remaining queries. This system card focuses primarily on gpt-5-thinking and gpt-5-main, while evaluations for other models are available in the appendix. The GPT-5 system not only outperforms previous models on benchmarks and answers questions more quickly, but -- more importantly -- is more useful for real-world queries. We've made significant advances in reducing hallucinations, improving instruction following, and minimizing sycophancy, and have leveled up GPT-5's performance in three of ChatGPT's most common uses: writing, coding, and health. All of the GPT-5 models additionally feature safe-completions, our latest approach to safety training to prevent disallowed content. Similarly to ChatGPT agent, we have decided to treat gpt-5-thinking as High capability in the Biological and Chemical domain under our Preparedness Framework, activating the associated safeguards. While we do not have definitive evidence that this model could meaningfully help a novice to create severe biological harm -- our defined threshold for High capability -- we have chosen to take a precautionary approach.

Swift for TensorFlow: A portable, flexible platform for deep learning

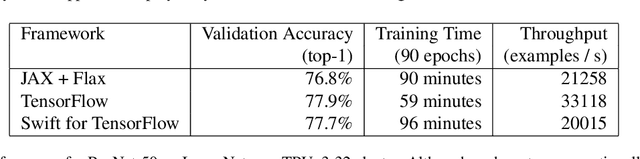
Swift for TensorFlow is a deep learning platform that scales from mobile devices to clusters of hardware accelerators in data centers. It combines a language-integrated automatic differentiation system and multiple Tensor implementations within a modern ahead-of-time compiled language oriented around mutable value semantics. The resulting platform has been validated through use in over 30 deep learning models and has been employed across data center and mobile applications.

Synthesizing Tasks for Block-based Programming

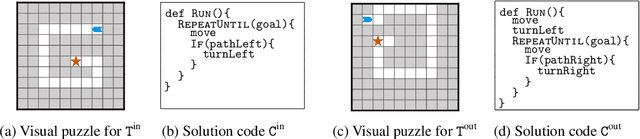
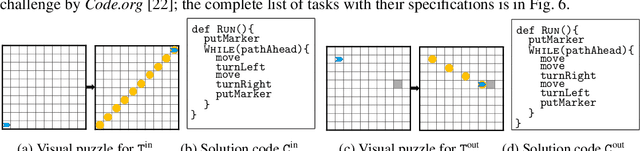
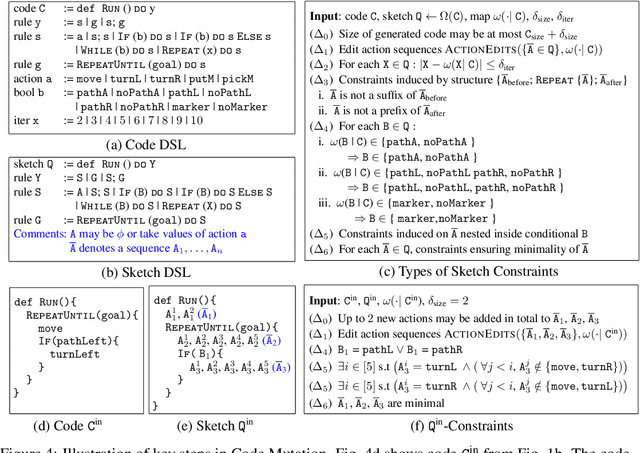
Block-based visual programming environments play a critical role in introducing computing concepts to K-12 students. One of the key pedagogical challenges in these environments is in designing new practice tasks for a student that match a desired level of difficulty and exercise specific programming concepts. In this paper, we formalize the problem of synthesizing visual programming tasks. In particular, given a reference visual task $\rm T^{in}$ and its solution code $\rm C^{in}$, we propose a novel methodology to automatically generate a set $\{(\rm T^{out}, \rm C^{out})\}$ of new tasks along with solution codes such that tasks $\rm T^{in}$ and $\rm T^{out}$ are conceptually similar but visually dissimilar. Our methodology is based on the realization that the mapping from the space of visual tasks to their solution codes is highly discontinuous; hence, directly mutating reference task $\rm T^{in}$ to generate new tasks is futile. Our task synthesis algorithm operates by first mutating code $\rm C^{in}$ to obtain a set of codes $\{\rm C^{out}\}$. Then, the algorithm performs symbolic execution over a code $\rm C^{out}$ to obtain a visual task $\rm T^{out}$; this step uses the Monte Carlo Tree Search (MCTS) procedure to guide the search in the symbolic tree. We demonstrate the effectiveness of our algorithm through an extensive empirical evaluation and user study on reference tasks taken from the \emph{Hour of the Code: Classic Maze} challenge by \emph{Code.org} and the \emph{Intro to Programming with Karel} course by \emph{CodeHS.com}.

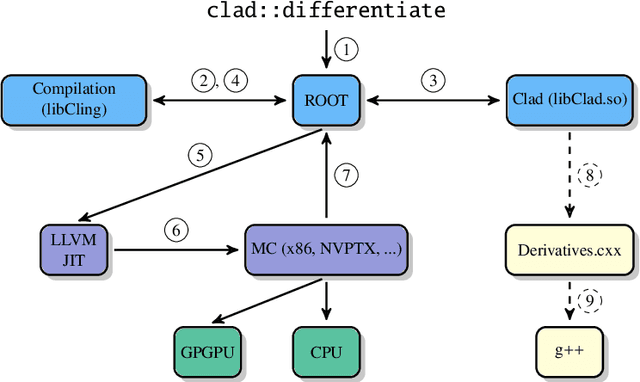
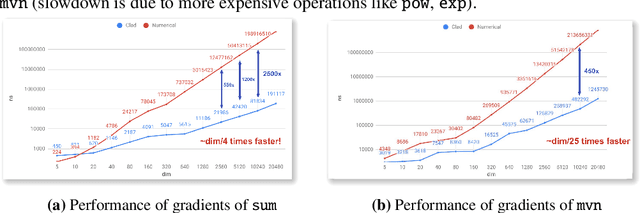
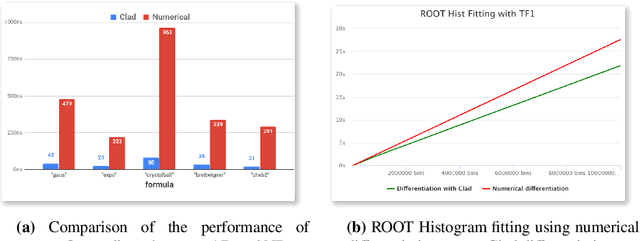
Automatic Differentiation in ROOT

In mathematics and computer algebra, automatic differentiation (AD) is a set of techniques to evaluate the derivative of a function specified by a computer program. AD exploits the fact that every computer program, no matter how complicated, executes a sequence of elementary arithmetic operations (addition, subtraction, multiplication, division, etc.), elementary functions (exp, log, sin, cos, etc.) and control flow statements. AD takes source code of a function as input and produces source code of the derived function. By applying the chain rule repeatedly to these operations, derivatives of arbitrary order can be computed automatically, accurately to working precision, and using at most a small constant factor more arithmetic operations than the original program. This paper presents AD techniques available in ROOT, supported by Cling, to produce derivatives of arbitrary C/C++ functions through implementing source code transformation and employing the chain rule of differential calculus in both forward mode and reverse mode. We explain its current integration for gradient computation in TFormula. We demonstrate the correctness and performance improvements in ROOT's fitting algorithms.