Leveraging State Space Models in Long Range Genomics

Long-range dependencies are critical for understanding genomic structure and function, yet most conventional methods struggle with them. Widely adopted transformer-based models, while excelling at short-context tasks, are limited by the attention module's quadratic computational complexity and inability to extrapolate to sequences longer than those seen in training. In this work, we explore State Space Models (SSMs) as a promising alternative by benchmarking two SSM-inspired architectures, Caduceus and Hawk, on long-range genomics modeling tasks under conditions parallel to a 50M parameter transformer baseline. We discover that SSMs match transformer performance and exhibit impressive zero-shot extrapolation across multiple tasks, handling contexts 10 to 100 times longer than those seen during training, indicating more generalizable representations better suited for modeling the long and complex human genome. Moreover, we demonstrate that these models can efficiently process sequences of 1M tokens on a single GPU, allowing for modeling entire genomic regions at once, even in labs with limited compute. Our findings establish SSMs as efficient and scalable for long-context genomic analysis.

Scaling Properties of Deep Residual Networks

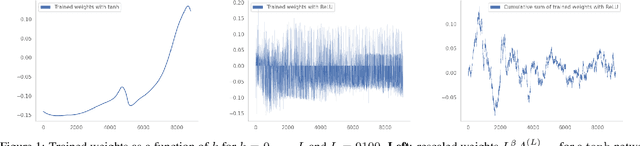
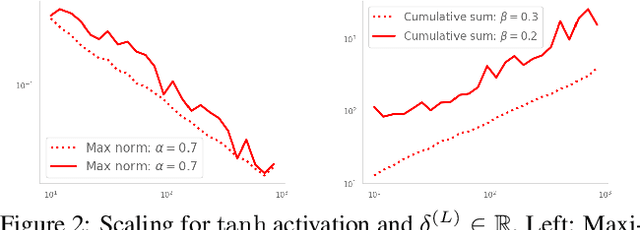
Residual networks (ResNets) have displayed impressive results in pattern recognition and, recently, have garnered considerable theoretical interest due to a perceived link with neural ordinary differential equations (neural ODEs). This link relies on the convergence of network weights to a smooth function as the number of layers increases. We investigate the properties of weights trained by stochastic gradient descent and their scaling with network depth through detailed numerical experiments. We observe the existence of scaling regimes markedly different from those assumed in neural ODE literature. Depending on certain features of the network architecture, such as the smoothness of the activation function, one may obtain an alternative ODE limit, a stochastic differential equation or neither of these. These findings cast doubts on the validity of the neural ODE model as an adequate asymptotic description of deep ResNets and point to an alternative class of differential equations as a better description of the deep network limit.

Ranked Reward: Enabling Self-Play Reinforcement Learning for Combinatorial Optimization

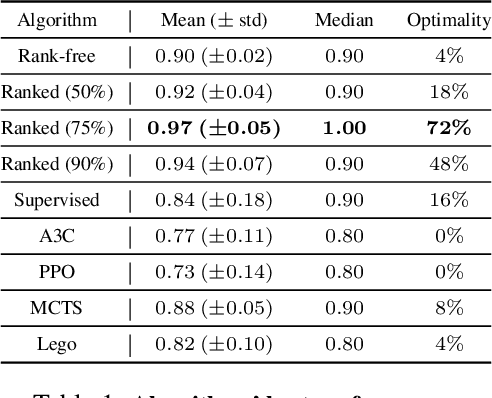
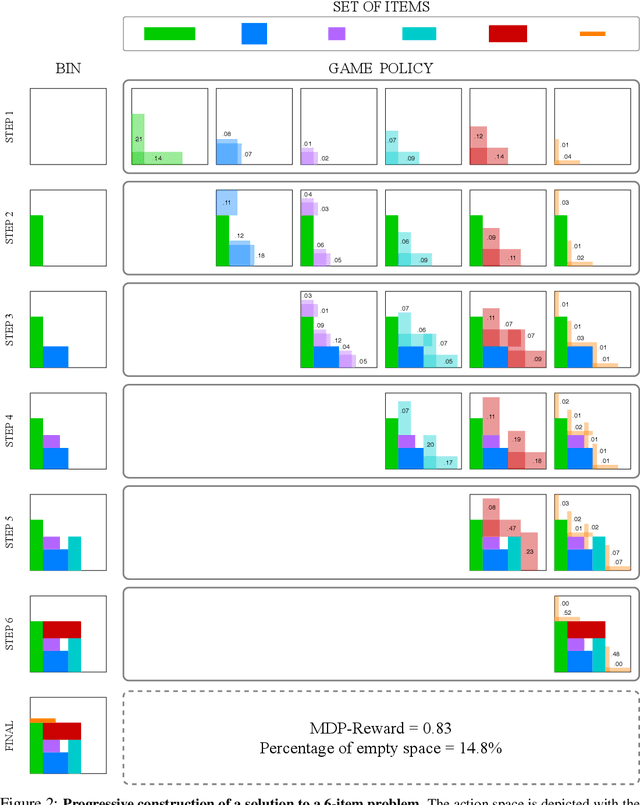
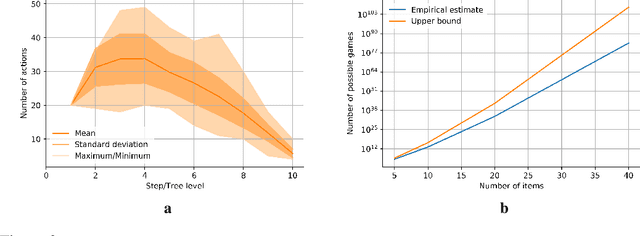
Adversarial self-play in two-player games has delivered impressive results when used with reinforcement learning algorithms that combine deep neural networks and tree search. Algorithms like AlphaZero and Expert Iteration learn tabula-rasa, producing highly informative training data on the fly. However, the self-play training strategy is not directly applicable to single-player games. Recently, several practically important combinatorial optimization problems, such as the traveling salesman problem and the bin packing problem, have been reformulated as reinforcement learning problems, increasing the importance of enabling the benefits of self-play beyond two-player games. We present the Ranked Reward (R2) algorithm which accomplishes this by ranking the rewards obtained by a single agent over multiple games to create a relative performance metric. Results from applying the R2 algorithm to instances of a two-dimensional bin packing problem show that it outperforms generic Monte Carlo tree search, heuristic algorithms and reinforcement learning algorithms not using ranked rewards.