Solving MAP Exactly using Systematic Search

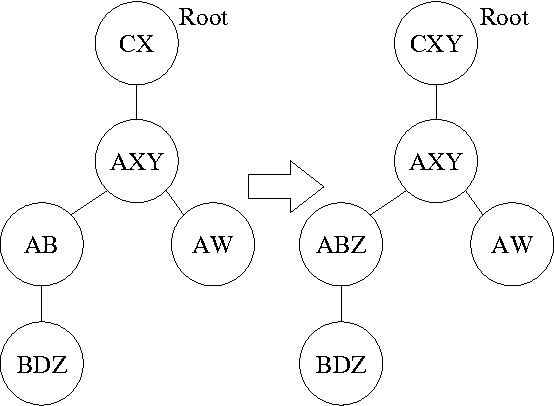
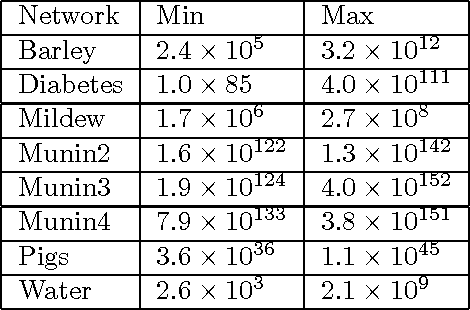
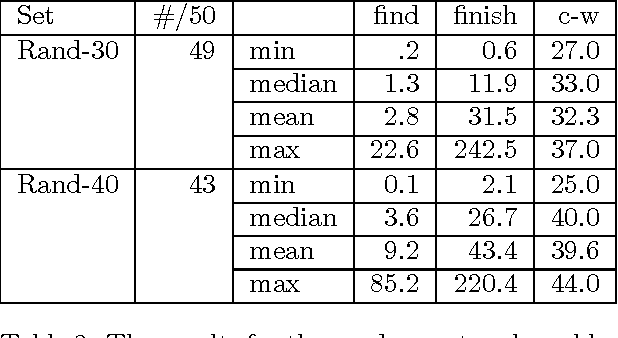
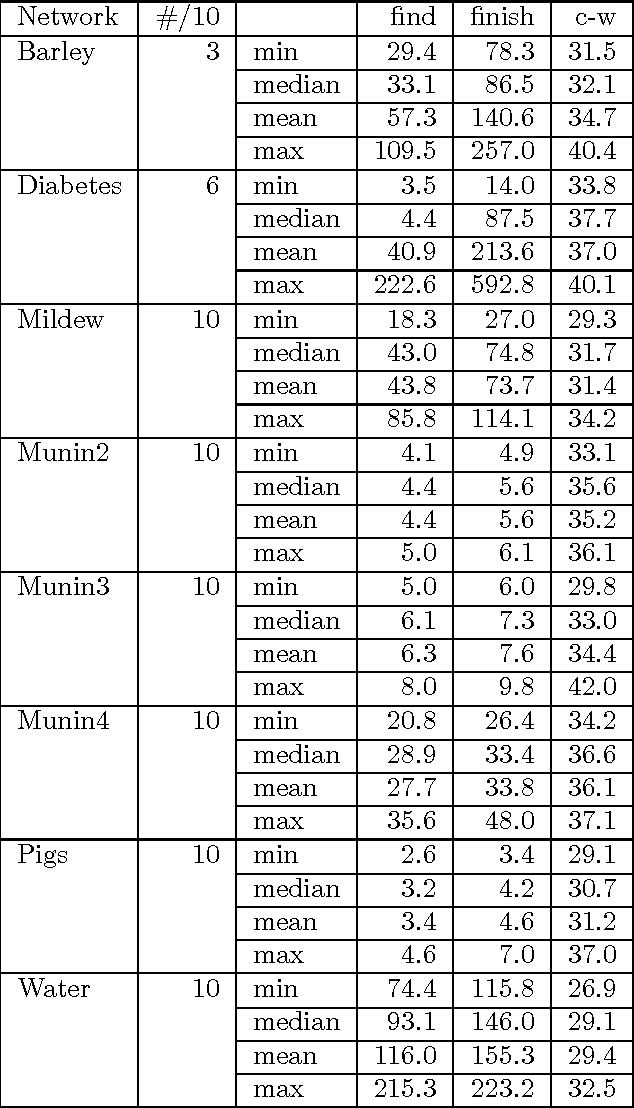
MAP is the problem of finding a most probable instantiation of a set of variables in a Bayesian network given some evidence. Unlike computing posterior probabilities, or MPE (a special case of MAP), the time and space complexity of structural solutions for MAP are not only exponential in the network treewidth, but in a larger parameter known as the "constrained" treewidth. In practice, this means that computing MAP can be orders of magnitude more expensive than computing posterior probabilities or MPE. This paper introduces a new, simple upper bound on the probability of a MAP solution, which admits a tradeoff between the bound quality and the time needed to compute it. The bound is shown to be generally much tighter than those of other methods of comparable complexity. We use this proposed upper bound to develop a branch-and-bound search algorithm for solving MAP exactly. Experimental results demonstrate that the search algorithm is able to solve many problems that are far beyond the reach of any structure-based method for MAP. For example, we show that the proposed algorithm can compute MAP exactly and efficiently for some networks whose constrained treewidth is more than 40.

Reasoning about Bayesian Network Classifiers

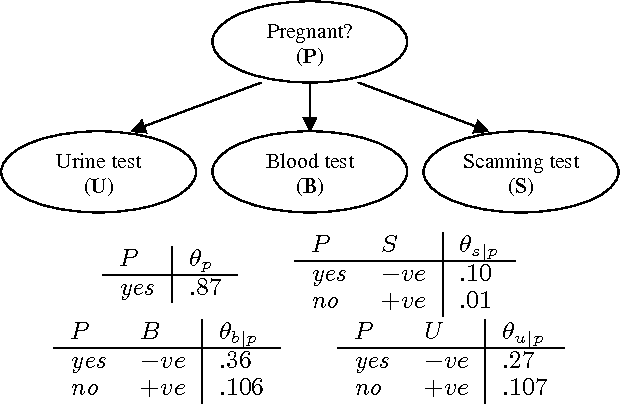
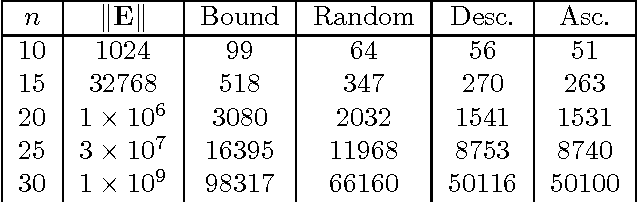
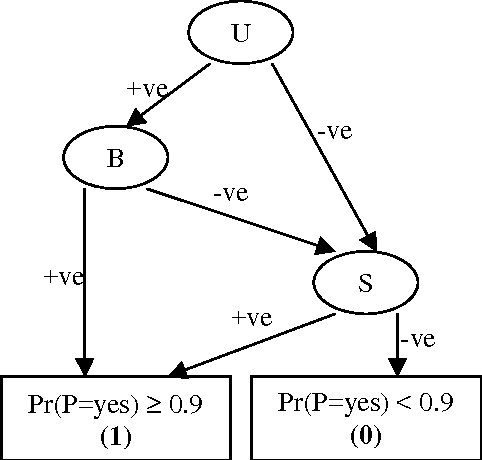
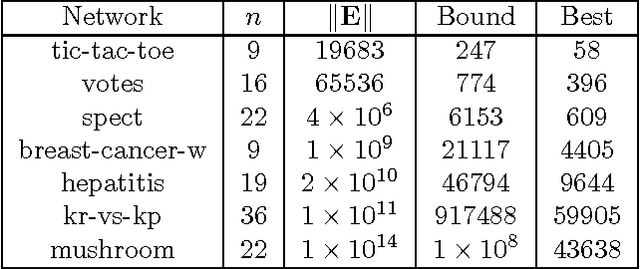
Bayesian network classifiers are used in many fields, and one common class of classifiers are naive Bayes classifiers. In this paper, we introduce an approach for reasoning about Bayesian network classifiers in which we explicitly convert them into Ordered Decision Diagrams (ODDs), which are then used to reason about the properties of these classifiers. Specifically, we present an algorithm for converting any naive Bayes classifier into an ODD, and we show theoretically and experimentally that this algorithm can give us an ODD that is tractable in size even given an intractable number of instances. Since ODDs are tractable representations of classifiers, our algorithm allows us to efficiently test the equivalence of two naive Bayes classifiers and characterize discrepancies between them. We also show a number of additional results including a count of distinct classifiers that can be induced by changing some CPT in a naive Bayes classifier, and the range of allowable changes to a CPT which keeps the current classifier unchanged.

New Advances in Inference by Recursive Conditioning

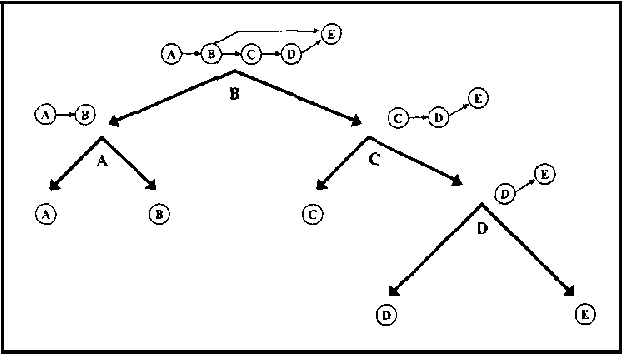
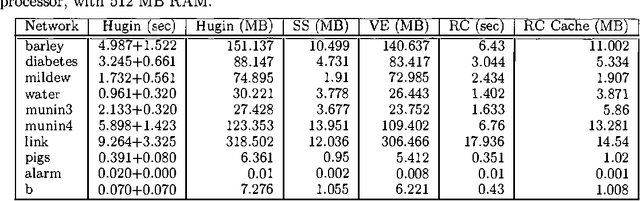
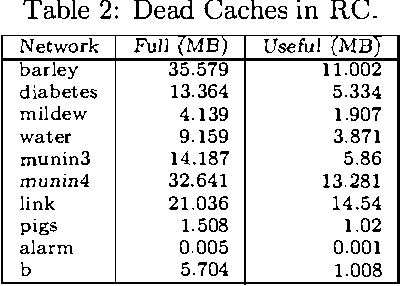
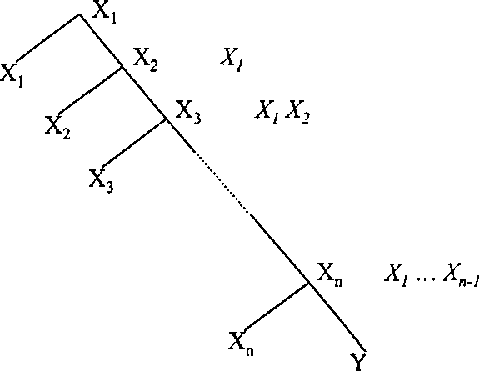
Recursive Conditioning (RC) was introduced recently as the first any-space algorithm for inference in Bayesian networks which can trade time for space by varying the size of its cache at the increment needed to store a floating point number. Under full caching, RC has an asymptotic time and space complexity which is comparable to mainstream algorithms based on variable elimination and clustering (exponential in the network treewidth and linear in its size). We show two main results about RC in this paper. First, we show that its actual space requirements under full caching are much more modest than those needed by mainstream methods and study the implications of this finding. Second, we show that RC can effectively deal with determinism in Bayesian networks by employing standard logical techniques, such as unit resolution, allowing a significant reduction in its time requirements in certain cases. We illustrate our results using a number of benchmark networks, including the very challenging ones that arise in genetic linkage analysis.

New Advances and Theoretical Insights into EDML

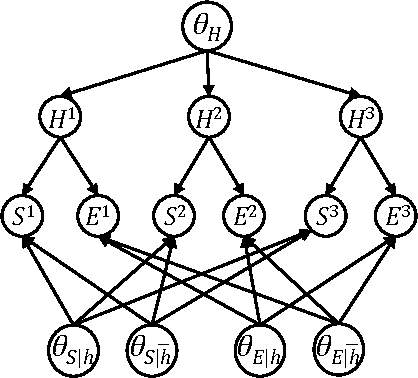
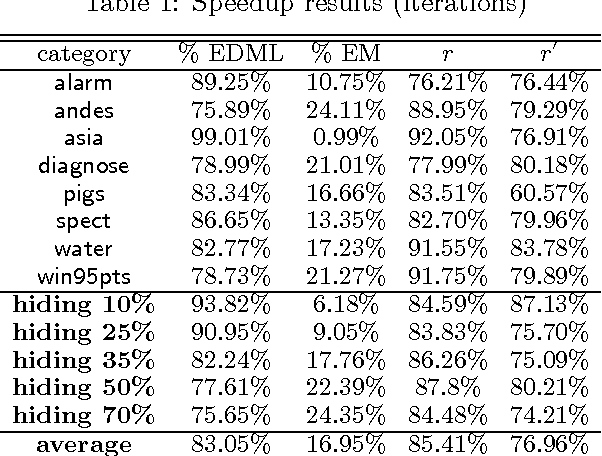
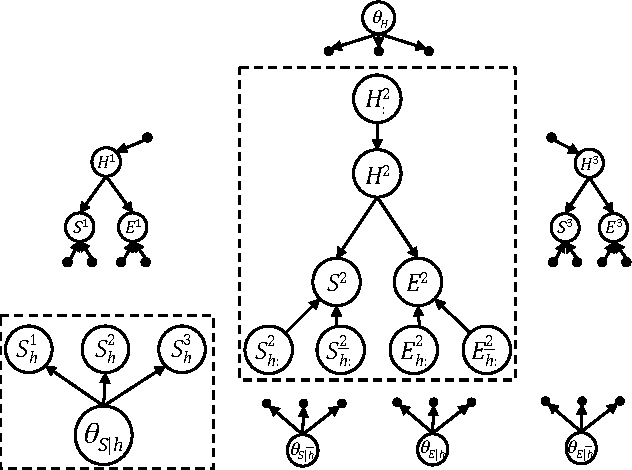
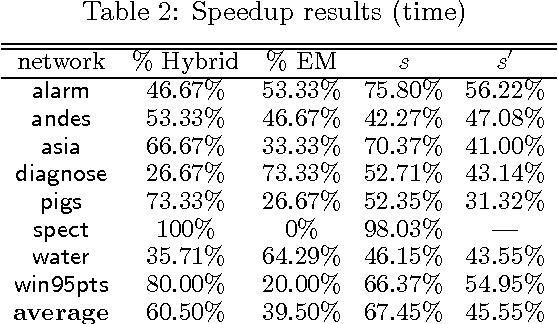
EDML is a recently proposed algorithm for learning MAP parameters in Bayesian networks. In this paper, we present a number of new advances and insights on the EDML algorithm. First, we provide the multivalued extension of EDML, originally proposed for Bayesian networks over binary variables. Next, we identify a simplified characterization of EDML that further implies a simple fixed-point algorithm for the convex optimization problem that underlies it. This characterization further reveals a connection between EDML and EM: a fixed point of EDML is a fixed point of EM, and vice versa. We thus identify also a new characterization of EM fixed points, but in the semantics of EDML. Finally, we propose a hybrid EDML/EM algorithm that takes advantage of the improved empirical convergence behavior of EDML, while maintaining the monotonic improvement property of EM.

Lifted Relax, Compensate and then Recover: From Approximate to Exact Lifted Probabilistic Inference

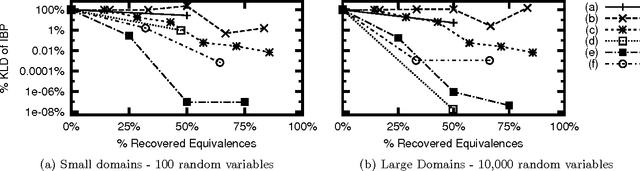
We propose an approach to lifted approximate inference for first-order probabilistic models, such as Markov logic networks. It is based on performing exact lifted inference in a simplified first-order model, which is found by relaxing first-order constraints, and then compensating for the relaxation. These simplified models can be incrementally improved by carefully recovering constraints that have been relaxed, also at the first-order level. This leads to a spectrum of approximations, with lifted belief propagation on one end, and exact lifted inference on the other. We discuss how relaxation, compensation, and recovery can be performed, all at the firstorder level, and show empirically that our approach substantially improves on the approximations of both propositional solvers and lifted belief propagation.

Sensitivity Analysis in Bayesian Networks: From Single to Multiple Parameters

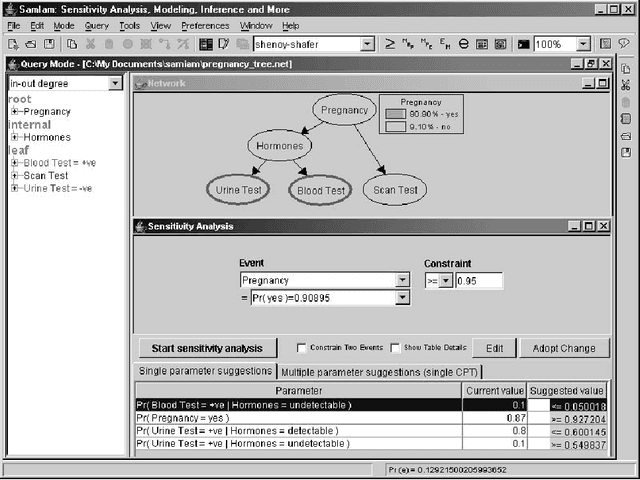
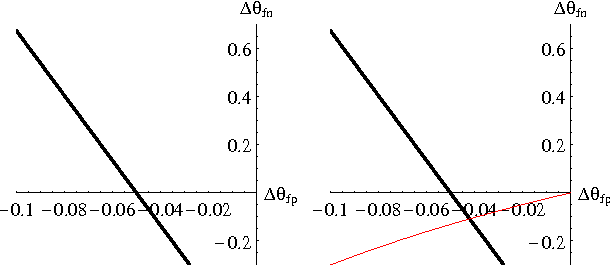
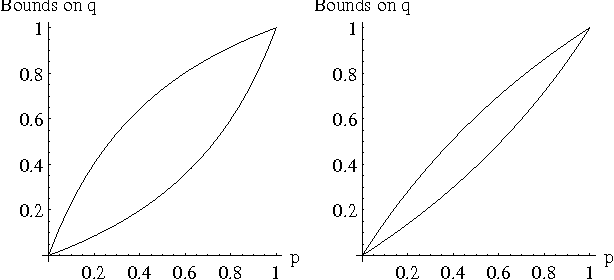
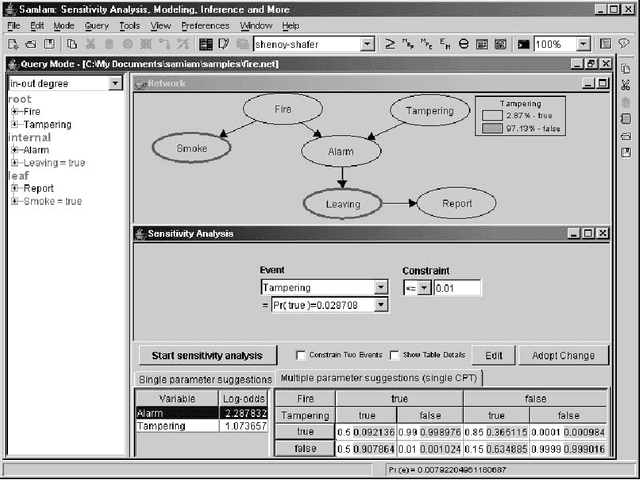
Previous work on sensitivity analysis in Bayesian networks has focused on single parameters, where the goal is to understand the sensitivity of queries to single parameter changes, and to identify single parameter changes that would enforce a certain query constraint. In this paper, we expand the work to multiple parameters which may be in the CPT of a single variable, or the CPTs of multiple variables. Not only do we identify the solution space of multiple parameter changes that would be needed to enforce a query constraint, but we also show how to find the optimal solution, that is, the one which disturbs the current probability distribution the least (with respect to a specific measure of disturbance). We characterize the computational complexity of our new techniques and discuss their applications to developing and debugging Bayesian networks, and to the problem of reasoning about the value (reliability) of new information.

Exploiting Evidence in Probabilistic Inference

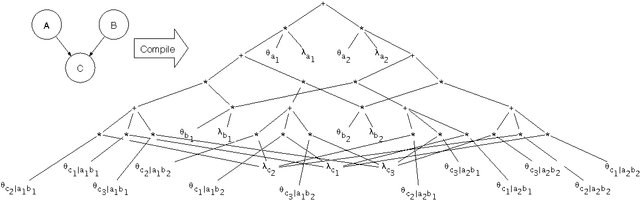
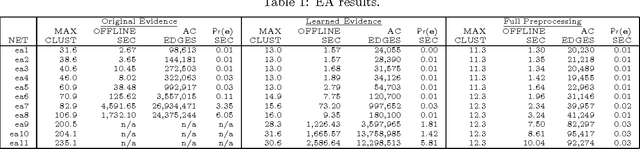
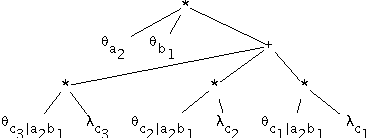
We define the notion of compiling a Bayesian network with evidence and provide a specific approach for evidence-based compilation, which makes use of logical processing. The approach is practical and advantageous in a number of application areas-including maximum likelihood estimation, sensitivity analysis, and MAP computations-and we provide specific empirical results in the domain of genetic linkage analysis. We also show that the approach is applicable for networks that do not contain determinism, and show that it empirically subsumes the performance of the quickscore algorithm when applied to noisy-or networks.

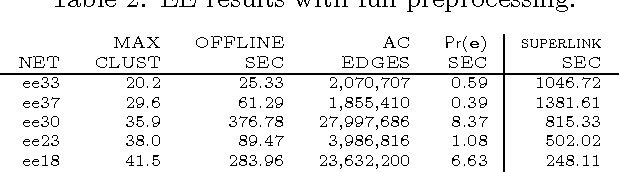
On Bayesian Network Approximation by Edge Deletion

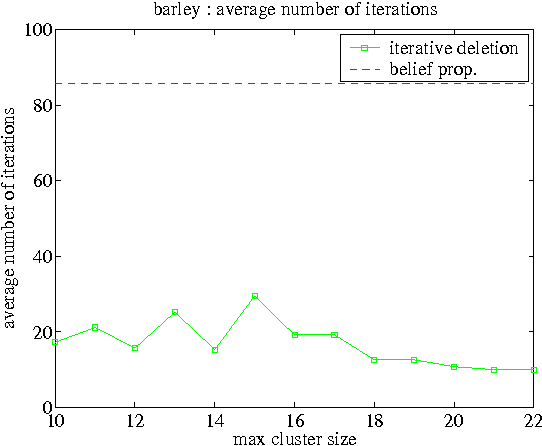
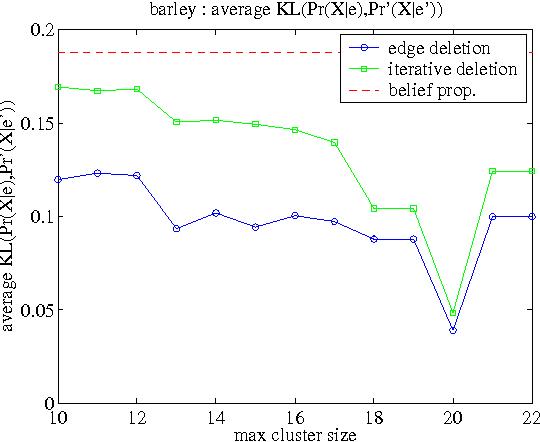
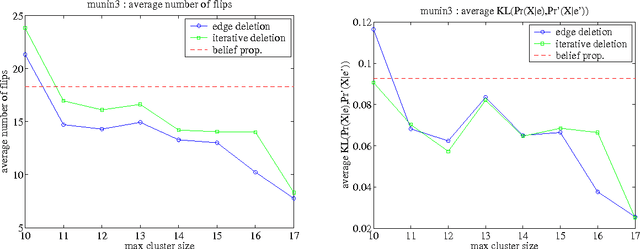
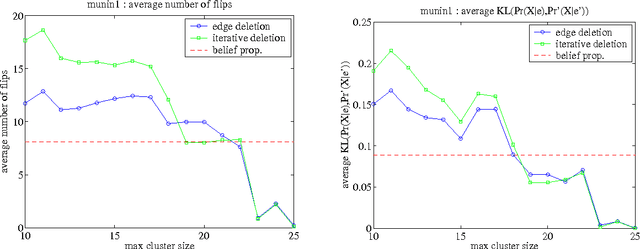
We consider the problem of deleting edges from a Bayesian network for the purpose of simplifying models in probabilistic inference. In particular, we propose a new method for deleting network edges, which is based on the evidence at hand. We provide some interesting bounds on the KL-divergence between original and approximate networks, which highlight the impact of given evidence on the quality of approximation and shed some light on good and bad candidates for edge deletion. We finally demonstrate empirically the promise of the proposed edge deletion technique as a basis for approximate inference.

On the Robustness of Most Probable Explanations

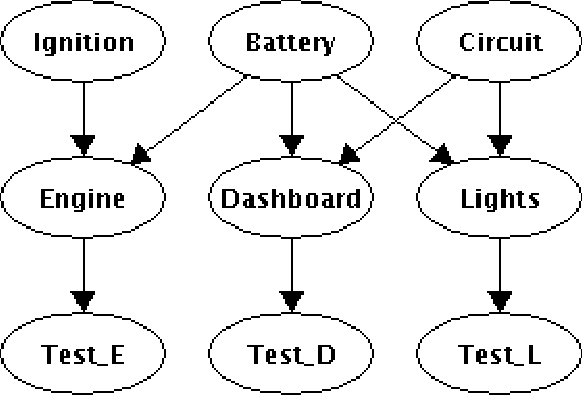
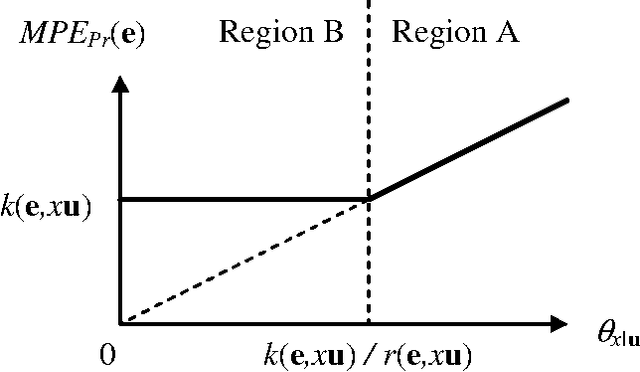
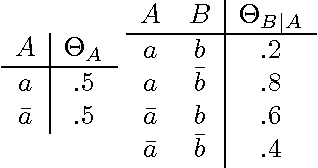
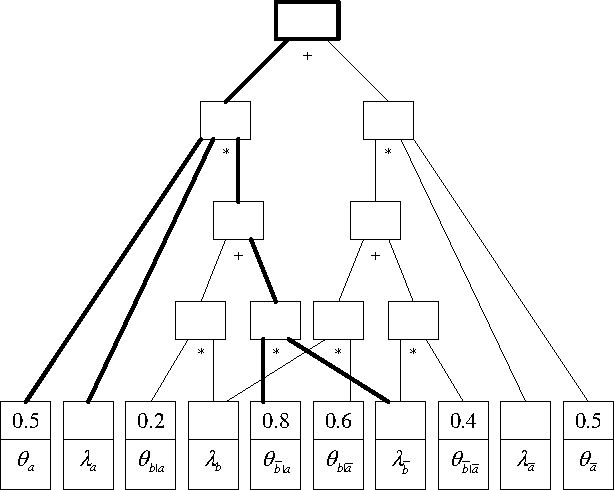
In Bayesian networks, a Most Probable Explanation (MPE) is a complete variable instantiation with a highest probability given the current evidence. In this paper, we discuss the problem of finding robustness conditions of the MPE under single parameter changes. Specifically, we ask the question: How much change in a single network parameter can we afford to apply while keeping the MPE unchanged? We will describe a procedure, which is the first of its kind, that computes this answer for each parameter in the Bayesian network variable in time O(n exp(w)), where n is the number of network variables and w is its treewidth.

A Variational Approach for Approximating Bayesian Networks by Edge Deletion

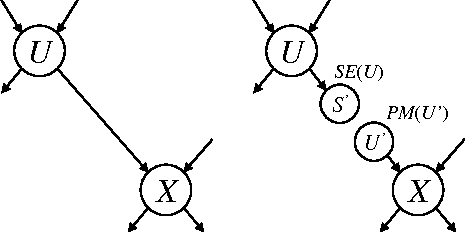
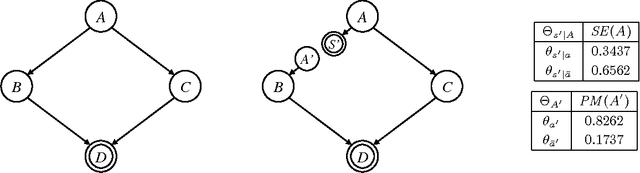
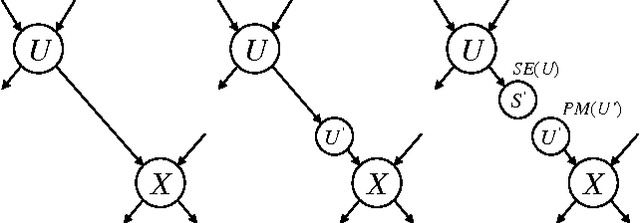
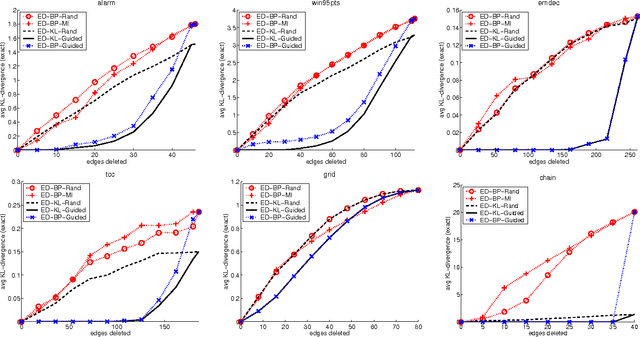
We consider in this paper the formulation of approximate inference in Bayesian networks as a problem of exact inference on an approximate network that results from deleting edges (to reduce treewidth). We have shown in earlier work that deleting edges calls for introducing auxiliary network parameters to compensate for lost dependencies, and proposed intuitive conditions for determining these parameters. We have also shown that our method corresponds to IBP when enough edges are deleted to yield a polytree, and corresponds to some generalizations of IBP when fewer edges are deleted. In this paper, we propose a different criteria for determining auxiliary parameters based on optimizing the KL-divergence between the original and approximate networks. We discuss the relationship between the two methods for selecting parameters, shedding new light on IBP and its generalizations. We also discuss the application of our new method to approximating inference problems which are exponential in constrained treewidth, including MAP and nonmyopic value of information.