James D. Park
Approximating MAP using Local Search
Jan 10, 2013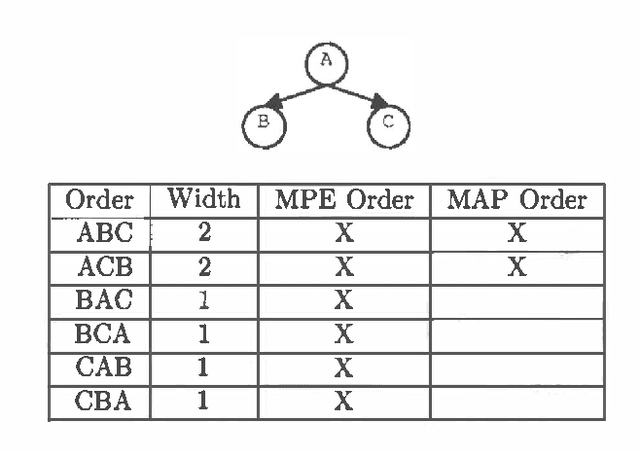
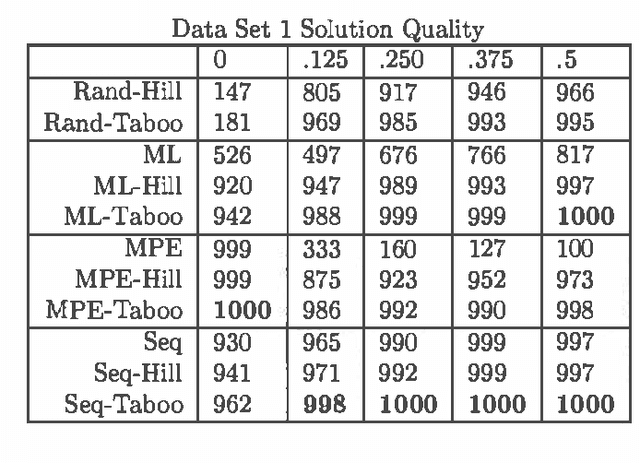
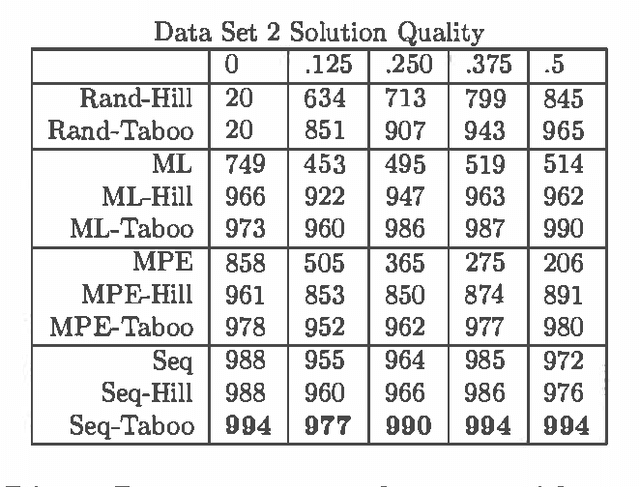
Abstract:MAP is the problem of finding a most probable instantiation of a set of variables in a Bayesian network, given evidence. Unlike computing marginals, posteriors, and MPE (a special case of MAP), the time and space complexity of MAP is not only exponential in the network treewidth, but also in a larger parameter known as the "constrained" treewidth. In practice, this means that computing MAP can be orders of magnitude more expensive than computingposteriors or MPE. Thus, practitioners generally avoid MAP computations, resorting instead to approximating them by the most likely value for each MAP variableseparately, or by MPE.We present a method for approximating MAP using local search. This method has space complexity which is exponential onlyin the treewidth, as is the complexity of each search step. We investigate the effectiveness of different local searchmethods and several initialization strategies and compare them to otherapproximation schemes.Experimental results show that local search provides a much more accurate approximation of MAP, while requiring few search steps.Practically, this means that the complexity of local search is often exponential only in treewidth as opposed to the constrained treewidth, making approximating MAP as efficient as other computations.
MAP Complexity Results and Approximation Methods
Dec 12, 2012
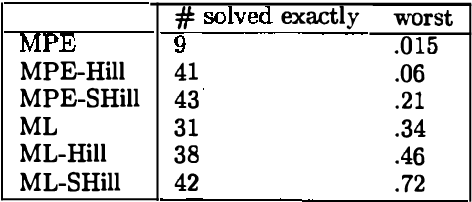
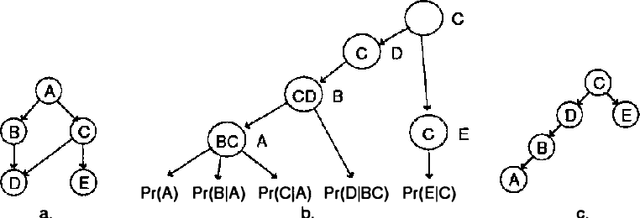

Abstract:MAP is the problem of finding a most probable instantiation of a set of nvariables in a Bayesian network, given some evidence. MAP appears to be a significantly harder problem than the related problems of computing the probability of evidence Pr, or MPE a special case of MAP. Because of the complexity of MAP, and the lack of viable algorithms to approximate it,MAP computations are generally avoided by practitioners. This paper investigates the complexity of MAP. We show that MAP is complete for NP. We also provide negative complexity results for elimination based algorithms. It turns out that MAP remains hard even when MPE, and Pr are easy. We show that MAP is NPcomplete when the networks are restricted to polytrees, and even then can not be effectively approximated. Because there is no approximation algorithm with guaranteed results, we investigate best effort approximations. We introduce a generic MAP approximation framework. As one instantiation of it, we implement local search coupled with belief propagation BP to approximate MAP. We show how to extract approximate evidence retraction information from belief propagation which allows us to perform efficient local search. This allows MAP approximation even on networks that are too complex to even exactly solve the easier problems of computing Pr or MPE. Experimental results indicate that using BP and local search provides accurate MAP estimates in many cases.
Solving MAP Exactly using Systematic Search
Oct 19, 2012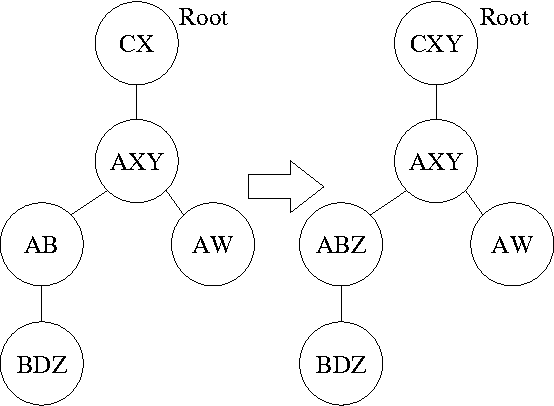
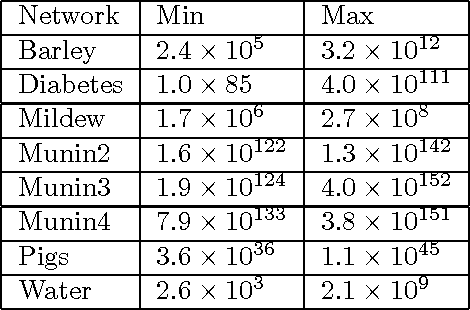
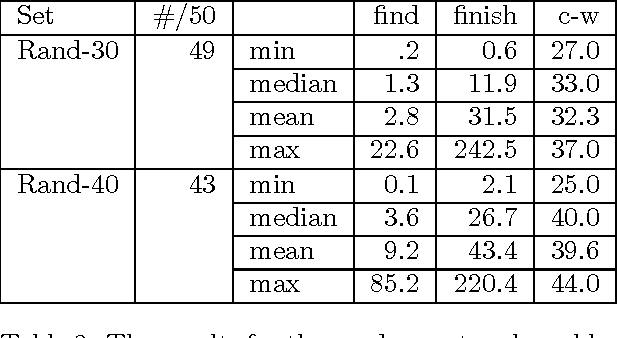
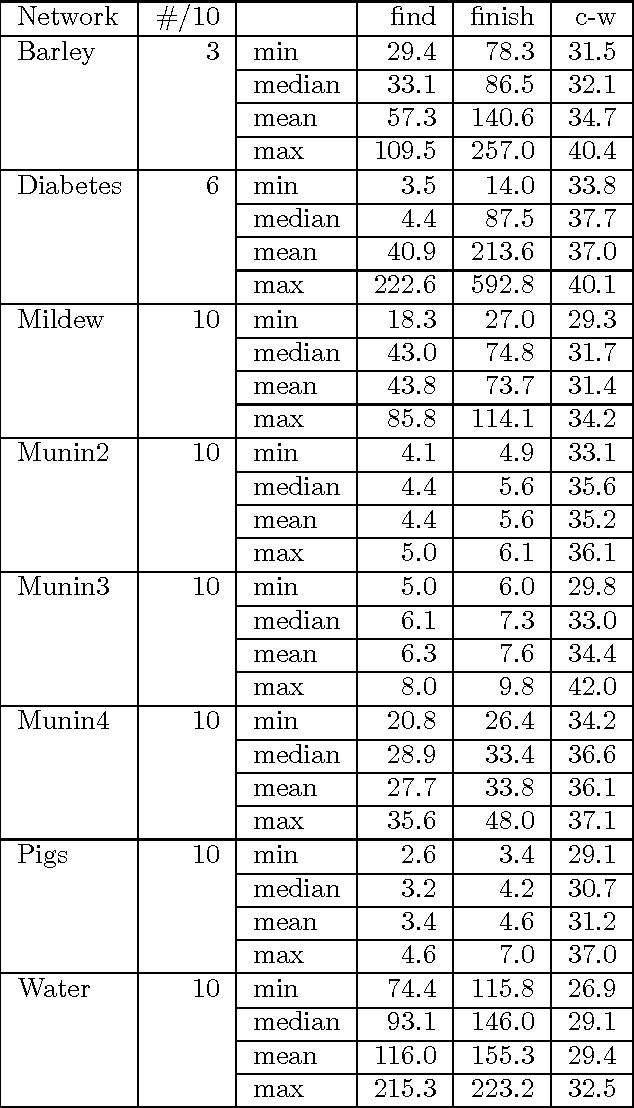
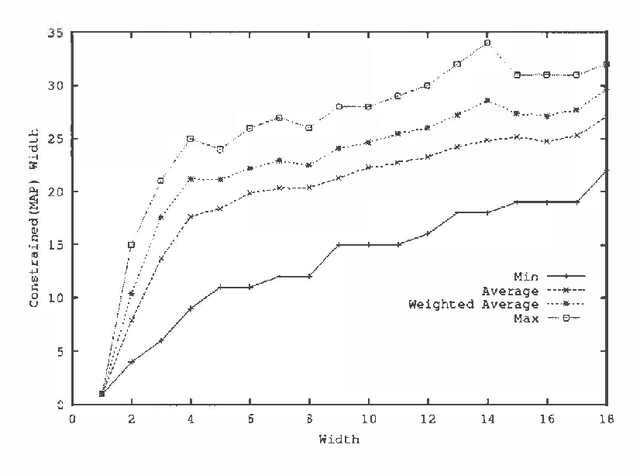
Abstract:MAP is the problem of finding a most probable instantiation of a set of variables in a Bayesian network given some evidence. Unlike computing posterior probabilities, or MPE (a special case of MAP), the time and space complexity of structural solutions for MAP are not only exponential in the network treewidth, but in a larger parameter known as the "constrained" treewidth. In practice, this means that computing MAP can be orders of magnitude more expensive than computing posterior probabilities or MPE. This paper introduces a new, simple upper bound on the probability of a MAP solution, which admits a tradeoff between the bound quality and the time needed to compute it. The bound is shown to be generally much tighter than those of other methods of comparable complexity. We use this proposed upper bound to develop a branch-and-bound search algorithm for solving MAP exactly. Experimental results demonstrate that the search algorithm is able to solve many problems that are far beyond the reach of any structure-based method for MAP. For example, we show that the proposed algorithm can compute MAP exactly and efficiently for some networks whose constrained treewidth is more than 40.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge