Constrained Linear Thompson Sampling

We study the safe linear bandit problem, where an agent sequentially selects actions from a convex domain to maximize an unknown objective while ensuring unknown linear constraints are satisfied on a per-round basis. Existing approaches primarily rely on optimism-based methods with frequentist confidence bounds, often leading to computationally expensive action selection routines. We propose COnstrained Linear Thompson Sampling (COLTS), a sampling-based framework that efficiently balances regret minimization and constraint satisfaction by selecting actions on the basis of noisy perturbations of the estimates of the unknown objective vector and constraint matrix. We introduce three variants of COLTS, distinguished by the learner's available side information: - S-COLTS assumes access to a known safe action and ensures strict constraint enforcement by combining the COLTS approach with a rescaling towards the safe action. For $d$-dimensional actions, this yields $\tilde{O}(\sqrt{d^3 T})$ regret and zero constraint violations (or risk). - E-COLTS enforces constraints softly under Slater's condition, and attains regret and risk of $\tilde{O}(\sqrt{d^3 T})$ by combining COLTS with uniform exploration. - R-COLTS requires no side information, and ensures instance-independent regret and risk of $\tilde{O}(\sqrt{d^3 T})$ by leveraging repeated resampling. A key technical innovation is a coupled noise design, which maintains optimism while preserving computational efficiency, which is combined with a scaling based analysis technique to address the variation of the per-round feasible region induced by sampled constraint matrices. Our methods match the regret bounds of prior approaches, while significantly reducing computational costs compared to them, thus yielding a scalable and practical approach for constrained bandit linear optimization.

SPARC: Score Prompting and Adaptive Fusion for Zero-Shot Multi-Label Recognition in Vision-Language Models

Zero-shot multi-label recognition (MLR) with Vision-Language Models (VLMs) faces significant challenges without training data, model tuning, or architectural modifications. Existing approaches require prompt tuning or architectural adaptations, limiting zero-shot applicability. Our work proposes a novel solution treating VLMs as black boxes, leveraging scores without training data or ground truth. Using large language model insights on object co-occurrence, we introduce compound prompts grounded in realistic object combinations. Analysis of these prompt scores reveals VLM biases and ``AND''/``OR'' signal ambiguities, notably that maximum compound scores are surprisingly suboptimal compared to second-highest scores. We address these through a debiasing and score-fusion algorithm that corrects image bias and clarifies VLM response behaviors. Our method enhances other zero-shot approaches, consistently improving their results. Experiments show superior mean Average Precision (mAP) compared to methods requiring training data, achieved through refined object ranking for robust zero-shot MLR.

Label Noise: Ignorance Is Bliss

We establish a new theoretical framework for learning under multi-class, instance-dependent label noise. This framework casts learning with label noise as a form of domain adaptation, in particular, domain adaptation under posterior drift. We introduce the concept of \emph{relative signal strength} (RSS), a pointwise measure that quantifies the transferability from noisy to clean posterior. Using RSS, we establish nearly matching upper and lower bounds on the excess risk. Our theoretical findings support the simple \emph{Noise Ignorant Empirical Risk Minimization (NI-ERM)} principle, which minimizes empirical risk while ignoring label noise. Finally, we translate this theoretical insight into practice: by using NI-ERM to fit a linear classifier on top of a self-supervised feature extractor, we achieve state-of-the-art performance on the CIFAR-N data challenge.

Testing the Feasibility of Linear Programs with Bandit Feedback

While the recent literature has seen a surge in the study of constrained bandit problems, all existing methods for these begin by assuming the feasibility of the underlying problem. We initiate the study of testing such feasibility assumptions, and in particular address the problem in the linear bandit setting, thus characterising the costs of feasibility testing for an unknown linear program using bandit feedback. Concretely, we test if $\exists x: Ax \ge 0$ for an unknown $A \in \mathbb{R}^{m \times d}$, by playing a sequence of actions $x_t\in \mathbb{R}^d$, and observing $Ax_t + \mathrm{noise}$ in response. By identifying the hypothesis as determining the sign of the value of a minimax game, we construct a novel test based on low-regret algorithms and a nonasymptotic law of iterated logarithms. We prove that this test is reliable, and adapts to the `signal level,' $\Gamma,$ of any instance, with mean sample costs scaling as $\widetilde{O}(d^2/\Gamma^2)$. We complement this by a minimax lower bound of $\Omega(d/\Gamma^2)$ for sample costs of reliable tests, dominating prior asymptotic lower bounds by capturing the dependence on $d$, and thus elucidating a basic insight missing in the extant literature on such problems.

Counterfactually Comparing Abstaining Classifiers

Abstaining classifiers have the option to abstain from making predictions on inputs that they are unsure about. These classifiers are becoming increasingly popular in high-stake decision-making problems, as they can withhold uncertain predictions to improve their reliability and safety. When evaluating black-box abstaining classifier(s), however, we lack a principled approach that accounts for what the classifier would have predicted on its abstentions. These missing predictions are crucial when, e.g., a radiologist is unsure of their diagnosis or when a driver is inattentive in a self-driving car. In this paper, we introduce a novel approach and perspective to the problem of evaluating and comparing abstaining classifiers by treating abstentions as missing data. Our evaluation approach is centered around defining the counterfactual score of an abstaining classifier, defined as the expected performance of the classifier had it not been allowed to abstain. We specify the conditions under which the counterfactual score is identifiable: if the abstentions are stochastic, and if the evaluation data is independent of the training data (ensuring that the predictions are missing at random), then the score is identifiable. Note that, if abstentions are deterministic, then the score is unidentifiable because the classifier can perform arbitrarily poorly on its abstentions. Leveraging tools from observational causal inference, we then develop nonparametric and doubly robust methods to efficiently estimate this quantity under identification. Our approach is examined in both simulated and real data experiments.

A Doubly Optimistic Strategy for Safe Linear Bandits

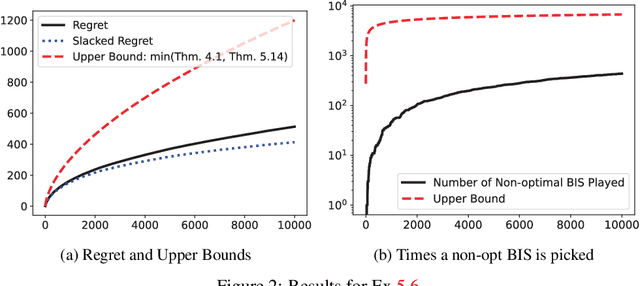
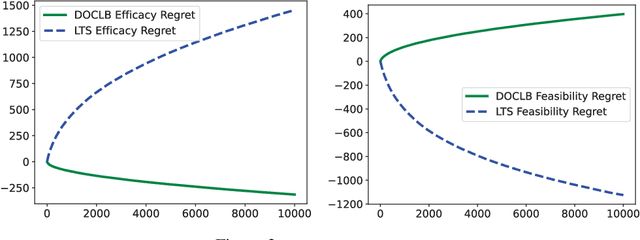
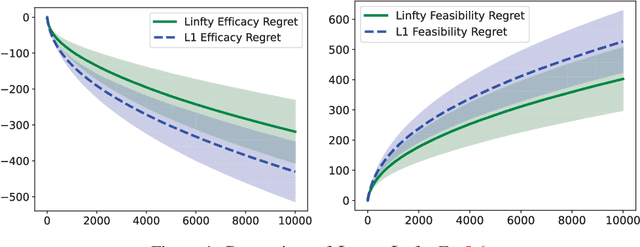
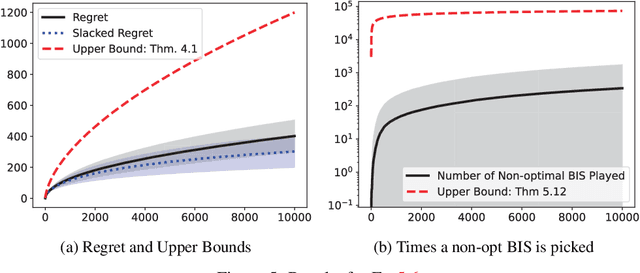
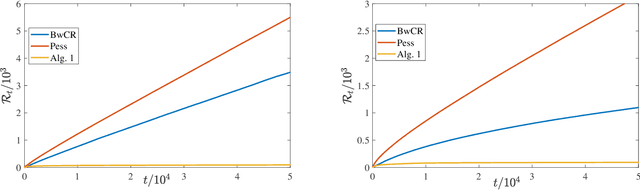
We propose a \underline{d}oubly \underline{o}ptimistic strategy for the \underline{s}afe-\underline{l}inear-\underline{b}andit problem, DOSLB. The safe linear bandit problem is to optimise an unknown linear reward whilst satisfying unknown round-wise safety constraints on actions, using stochastic bandit feedback of reward and safety-risks of actions. In contrast to prior work on aggregated resource constraints, our formulation explicitly demands control on roundwise safety risks. Unlike existing optimistic-pessimistic paradigms for safe bandits, DOSLB exercises supreme optimism, using optimistic estimates of reward and safety scores to select actions. Yet, and surprisingly, we show that DOSLB rarely takes risky actions, and obtains $\tilde{O}(d \sqrt{T})$ regret, where our notion of regret accounts for both inefficiency and lack of safety of actions. Specialising to polytopal domains, we first notably show that the $\sqrt{T}$-regret bound cannot be improved even with large gaps, and then identify a slackened notion of regret for which we show tight instance-dependent $O(\log^2 T)$ bounds. We further argue that in such domains, the number of times an overly risky action is played is also bounded as $O(\log^2T)$.

Strategies for Safe Multi-Armed Bandits with Logarithmic Regret and Risk

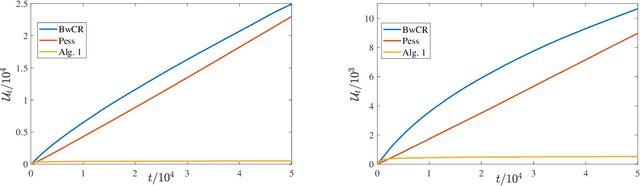
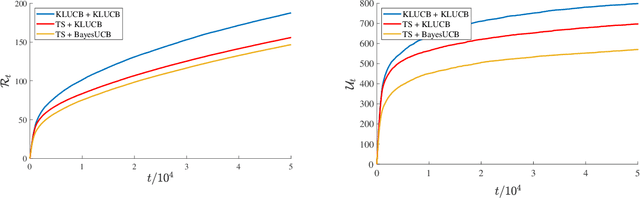
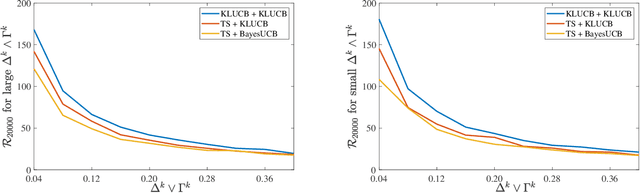
We investigate a natural but surprisingly unstudied approach to the multi-armed bandit problem under safety risk constraints. Each arm is associated with an unknown law on safety risks and rewards, and the learner's goal is to maximise reward whilst not playing unsafe arms, as determined by a given threshold on the mean risk. We formulate a pseudo-regret for this setting that enforces this safety constraint in a per-round way by softly penalising any violation, regardless of the gain in reward due to the same. This has practical relevance to scenarios such as clinical trials, where one must maintain safety for each round rather than in an aggregated sense. We describe doubly optimistic strategies for this scenario, which maintain optimistic indices for both safety risk and reward. We show that schema based on both frequentist and Bayesian indices satisfy tight gap-dependent logarithmic regret bounds, and further that these play unsafe arms only logarithmically many times in total. This theoretical analysis is complemented by simulation studies demonstrating the effectiveness of the proposed schema, and probing the domains in which their use is appropriate.

Online Selective Classification with Limited Feedback

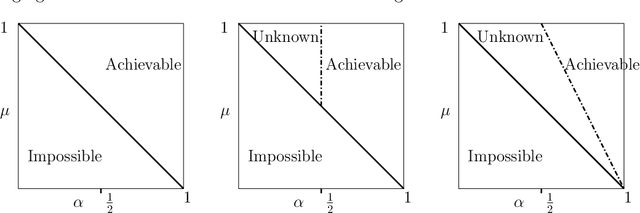
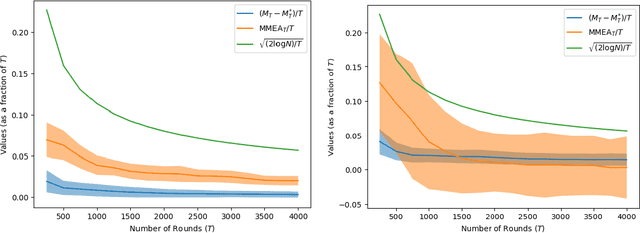
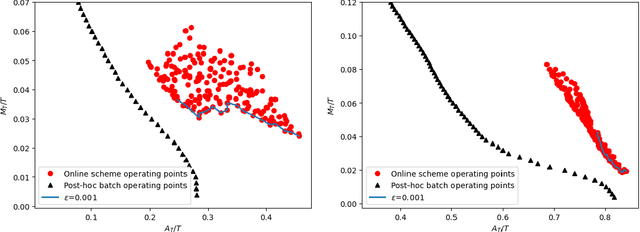
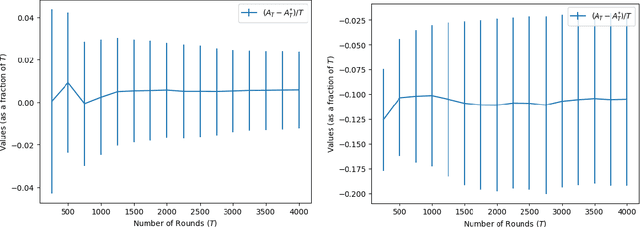
Motivated by applications to resource-limited and safety-critical domains, we study selective classification in the online learning model, wherein a predictor may abstain from classifying an instance. For example, this may model an adaptive decision to invoke more resources on this instance. Two salient aspects of the setting we consider are that the data may be non-realisable, due to which abstention may be a valid long-term action, and that feedback is only received when the learner abstains, which models the fact that reliable labels are only available when the resource intensive processing is invoked. Within this framework, we explore strategies that make few mistakes, while not abstaining too many times more than the best-in-hindsight error-free classifier from a given class. That is, the one that makes no mistakes, while abstaining the fewest number of times. We construct simple versioning-based schemes for any $\mu \in (0,1],$ that make most $T^\mu$ mistakes while incurring \smash{$\tilde{O}(T^{1-\mu})$} excess abstention against adaptive adversaries. We further show that this dependence on $T$ is tight, and provide illustrative experiments on realistic datasets.

Selective Classification via One-Sided Prediction

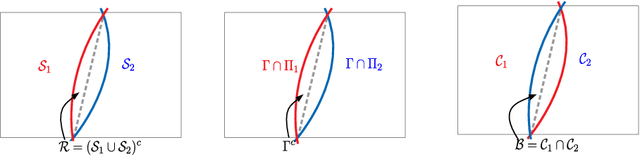
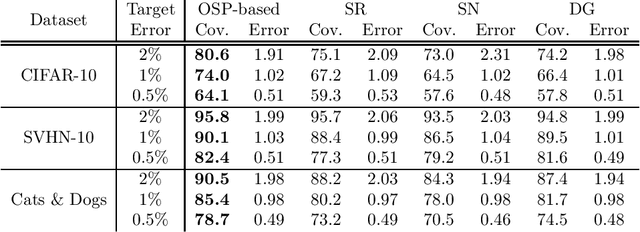
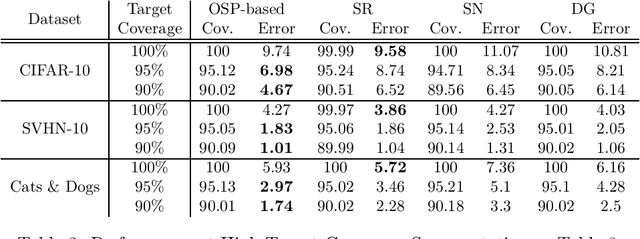
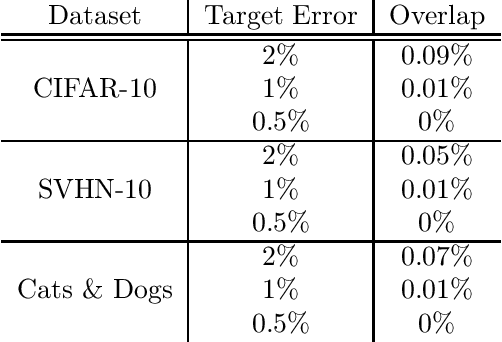
We propose a novel method for selective classification (SC), a problem which allows a classifier to abstain from predicting some instances, thus trading off accuracy against coverage (the fraction of instances predicted). In contrast to prior gating or confidence-set based work, our proposed method optimises a collection of class-wise decoupled one-sided empirical risks, and is in essence a method for explicitly finding the largest decision sets for each class that have few false positives. This one-sided prediction (OSP) based relaxation yields an SC scheme that attains near-optimal coverage in the practically relevant high target accuracy regime, and further admits efficient implementation, leading to a flexible and principled method for SC. We theoretically derive generalization bounds for SC and OSP, and empirically we show that our scheme strongly outperforms state of the art methods in coverage at small error levels.

Piecewise Linear Regression via a Difference of Convex Functions

We present a new piecewise linear regression methodology that utilizes fitting a difference of convex functions (DC functions) to the data. These are functions $f$ that may be represented as the difference $\phi_1 - \phi_2$ for a choice of convex functions $\phi_1, \phi_2$. The method proceeds by estimating piecewise-liner convex functions, in a manner similar to max-affine regression, whose difference approximates the data. The choice of the function is regularised by a new seminorm over the class of DC functions that controls the $\ell_\infty$ Lipschitz constant of the estimate. The resulting methodology can be efficiently implemented via Quadratic programming even in high dimensions, and is shown to have close to minimax statistical risk. We empirically validate the method, showing it to be practically implementable, and to have comparable performance to existing regression/classification methods on real-world datasets.