dcFCI: Robust Causal Discovery Under Latent Confounding, Unfaithfulness, and Mixed Data

Causal discovery is central to inferring causal relationships from observational data. In the presence of latent confounding, algorithms such as Fast Causal Inference (FCI) learn a Partial Ancestral Graph (PAG) representing the true model's Markov Equivalence Class. However, their correctness critically depends on empirical faithfulness, the assumption that observed (in)dependencies perfectly reflect those of the underlying causal model, which often fails in practice due to limited sample sizes. To address this, we introduce the first nonparametric score to assess a PAG's compatibility with observed data, even with mixed variable types. This score is both necessary and sufficient to characterize structural uncertainty and distinguish between distinct PAGs. We then propose data-compatible FCI (dcFCI), the first hybrid causal discovery algorithm to jointly address latent confounding, empirical unfaithfulness, and mixed data types. dcFCI integrates our score into an (Anytime)FCI-guided search that systematically explores, ranks, and validates candidate PAGs. Experiments on synthetic and real-world scenarios demonstrate that dcFCI significantly outperforms state-of-the-art methods, often recovering the true PAG even in small and heterogeneous datasets. Examining top-ranked PAGs further provides valuable insights into structural uncertainty, supporting more robust and informed causal reasoning and decision-making.

Effect Identification in Cluster Causal Diagrams

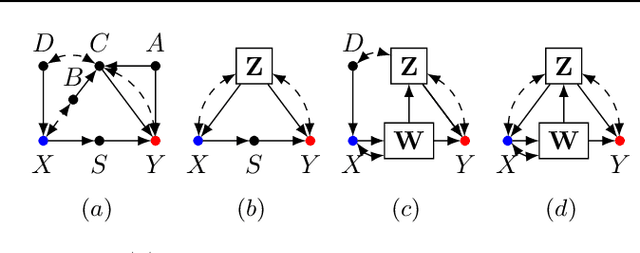
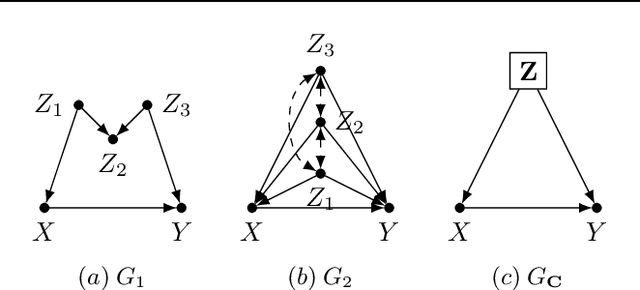
One pervasive task found throughout the empirical sciences is to determine the effect of interventions from non-experimental data. It is well-understood that assumptions are necessary to perform causal inferences, which are commonly articulated through causal diagrams (Pearl, 2000). Despite the power of this approach, there are settings where the knowledge necessary to specify a causal diagram over all observed variables may not be available, particularly in complex, high-dimensional domains. In this paper, we introduce a new type of graphical model called cluster causal diagrams (for short, C-DAGs) that allows for the partial specification of relationships among variables based on limited prior knowledge, alleviating the stringent requirement of specifying a full causal diagram. A C-DAG specifies relationships between clusters of variables, while the relationships between the variables within a cluster are left unspecified. We develop the foundations and machinery for valid causal inferences over C-DAGs. In particular, we first define a new version of the d-separation criterion and prove its soundness and completeness. Secondly, we extend these new separation rules and prove the validity of the corresponding do-calculus. Lastly, we show that a standard identification algorithm is sound and complete to systematically compute causal effects from observational data given a C-DAG.