Mixed Differential Privacy in Computer Vision

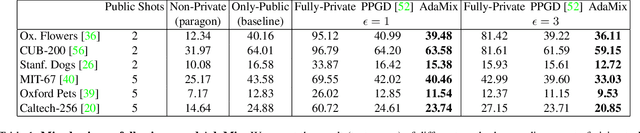
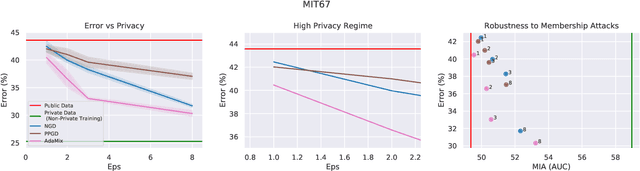
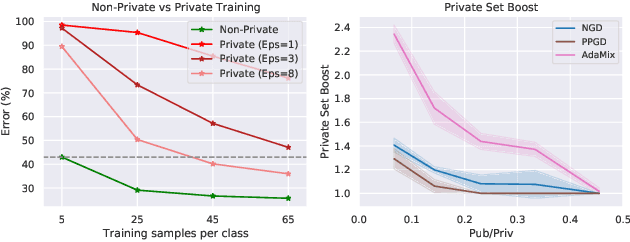
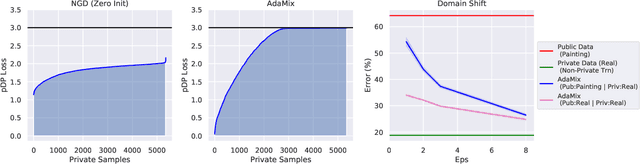
We introduce AdaMix, an adaptive differentially private algorithm for training deep neural network classifiers using both private and public image data. While pre-training language models on large public datasets has enabled strong differential privacy (DP) guarantees with minor loss of accuracy, a similar practice yields punishing trade-offs in vision tasks. A few-shot or even zero-shot learning baseline that ignores private data can outperform fine-tuning on a large private dataset. AdaMix incorporates few-shot training, or cross-modal zero-shot learning, on public data prior to private fine-tuning, to improve the trade-off. AdaMix reduces the error increase from the non-private upper bound from the 167-311\% of the baseline, on average across 6 datasets, to 68-92\% depending on the desired privacy level selected by the user. AdaMix tackles the trade-off arising in visual classification, whereby the most privacy sensitive data, corresponding to isolated points in representation space, are also critical for high classification accuracy. In addition, AdaMix comes with strong theoretical privacy guarantees and convergence analysis.

Beyond the Frontier: Fairness Without Accuracy Loss

Notions of fair machine learning that seek to control various kinds of error across protected groups generally are cast as constrained optimization problems over a fixed model class. For such problems, tradeoffs arise: asking for various kinds of technical fairness requires compromising on overall error, and adding more protected groups increases error rates across all groups. Our goal is to break though such accuracy-fairness tradeoffs. We develop a simple algorithmic framework that allows us to deploy models and then revise them dynamically when groups are discovered on which the error rate is suboptimal. Protected groups don't need to be pre-specified: At any point, if it is discovered that there is some group on which our current model performs substantially worse than optimally, then there is a simple update operation that improves the error on that group without increasing either overall error or the error on previously identified groups. We do not restrict the complexity of the groups that can be identified, and they can intersect in arbitrary ways. The key insight that allows us to break through the tradeoff barrier is to dynamically expand the model class as new groups are identified. The result is provably fast convergence to a model that can't be distinguished from the Bayes optimal predictor, at least by those tasked with finding high error groups. We explore two instantiations of this framework: as a "bias bug bounty" design in which external auditors are invited to discover groups on which our current model's error is suboptimal, and as an algorithmic paradigm in which the discovery of groups on which the error is suboptimal is posed as an optimization problem. In the bias bounty case, when we say that a model cannot be distinguished from Bayes optimal, we mean by any participant in the bounty program. We provide both theoretical analysis and experimental validation.

Online Multiobjective Minimax Optimization and Applications

We introduce a simple but general online learning framework, in which at every round, an adaptive adversary introduces a new game, consisting of an action space for the learner, an action space for the adversary, and a vector valued objective function that is convex-concave in every coordinate. The learner and the adversary then play in this game. The learner's goal is to play so as to minimize the maximum coordinate of the cumulative vector-valued loss. The resulting one-shot game is not convex-concave, and so the minimax theorem does not apply. Nevertheless, we give a simple algorithm that can compete with the setting in which the adversary must announce their action first, with optimally diminishing regret. We demonstrate the power of our simple framework by using it to derive optimal bounds and algorithms across a variety of domains. This includes no regret learning: we can recover optimal algorithms and bounds for minimizing external regret, internal regret, adaptive regret, multigroup regret, subsequence regret, and a notion of regret in the sleeping experts setting. Next, we use it to derive a variant of Blackwell's Approachability Theorem, which we term "Fast Polytope Approachability". Finally, we are able to recover recently derived algorithms and bounds for online adversarial multicalibration and related notions (mean-conditioned moment multicalibration, and prediction interval multivalidity).

Multiaccurate Proxies for Downstream Fairness

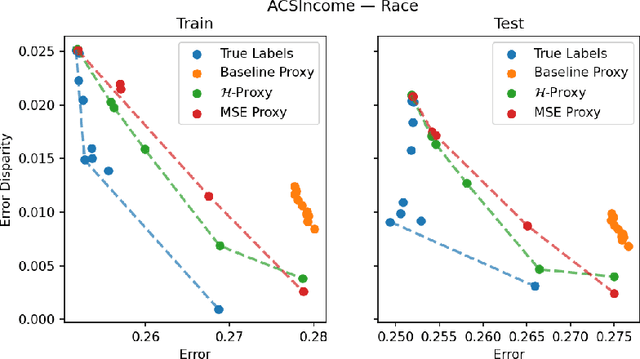
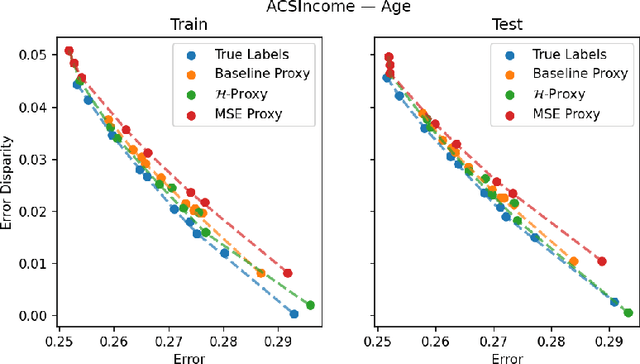
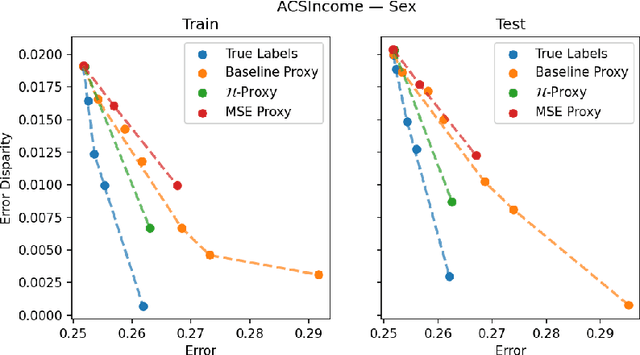
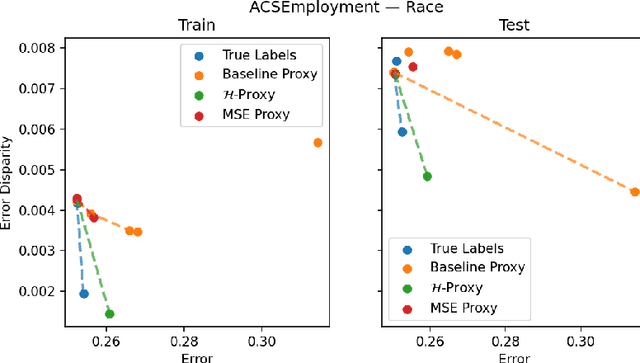
We study the problem of training a model that must obey demographic fairness conditions when the sensitive features are not available at training time -- in other words, how can we train a model to be fair by race when we don't have data about race? We adopt a fairness pipeline perspective, in which an "upstream" learner that does have access to the sensitive features will learn a proxy model for these features from the other attributes. The goal of the proxy is to allow a general "downstream" learner -- with minimal assumptions on their prediction task -- to be able to use the proxy to train a model that is fair with respect to the true sensitive features. We show that obeying multiaccuracy constraints with respect to the downstream model class suffices for this purpose, and provide sample- and oracle efficient-algorithms and generalization bounds for learning such proxies. In general, multiaccuracy can be much easier to satisfy than classification accuracy, and can be satisfied even when the sensitive features are hard to predict.

Adaptive Machine Unlearning

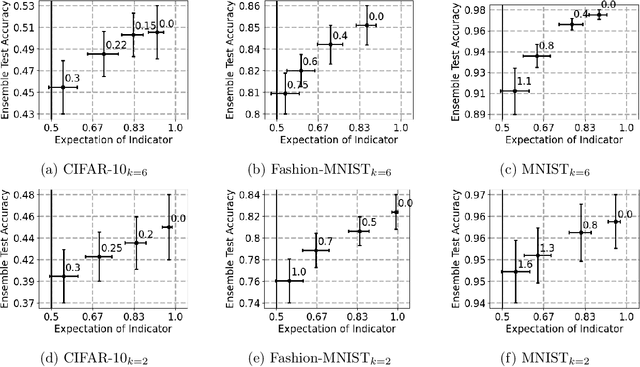
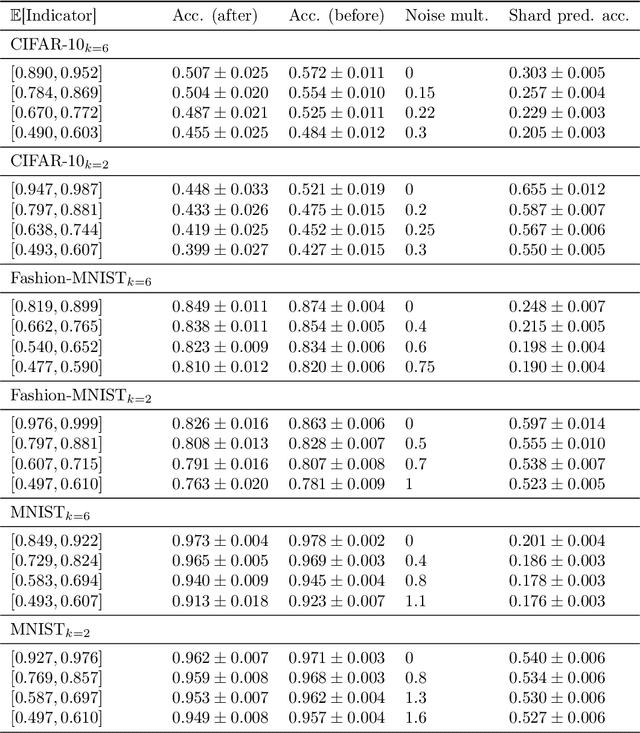
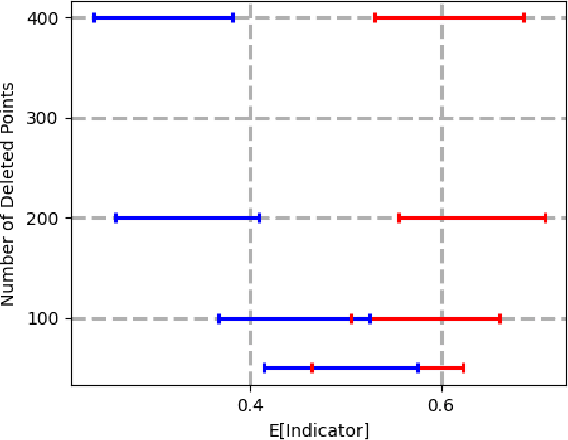
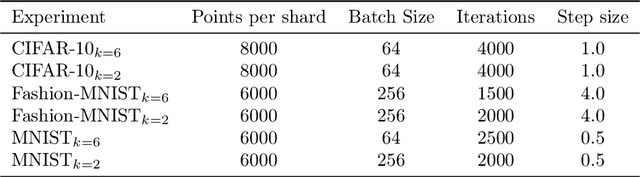
Data deletion algorithms aim to remove the influence of deleted data points from trained models at a cheaper computational cost than fully retraining those models. However, for sequences of deletions, most prior work in the non-convex setting gives valid guarantees only for sequences that are chosen independently of the models that are published. If people choose to delete their data as a function of the published models (because they don't like what the models reveal about them, for example), then the update sequence is adaptive. In this paper, we give a general reduction from deletion guarantees against adaptive sequences to deletion guarantees against non-adaptive sequences, using differential privacy and its connection to max information. Combined with ideas from prior work which give guarantees for non-adaptive deletion sequences, this leads to extremely flexible algorithms able to handle arbitrary model classes and training methodologies, giving strong provable deletion guarantees for adaptive deletion sequences. We show in theory how prior work for non-convex models fails against adaptive deletion sequences, and use this intuition to design a practical attack against the SISA algorithm of Bourtoule et al. [2021] on CIFAR-10, MNIST, Fashion-MNIST.

Rejoinder: Gaussian Differential Privacy

In this rejoinder, we aim to address two broad issues that cover most comments made in the discussion. First, we discuss some theoretical aspects of our work and comment on how this work might impact the theoretical foundation of privacy-preserving data analysis. Taking a practical viewpoint, we next discuss how f-differential privacy (f-DP) and Gaussian differential privacy (GDP) can make a difference in a range of applications.

Differentially Private Query Release Through Adaptive Projection

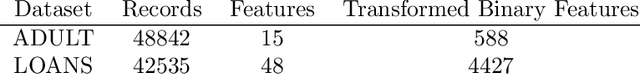
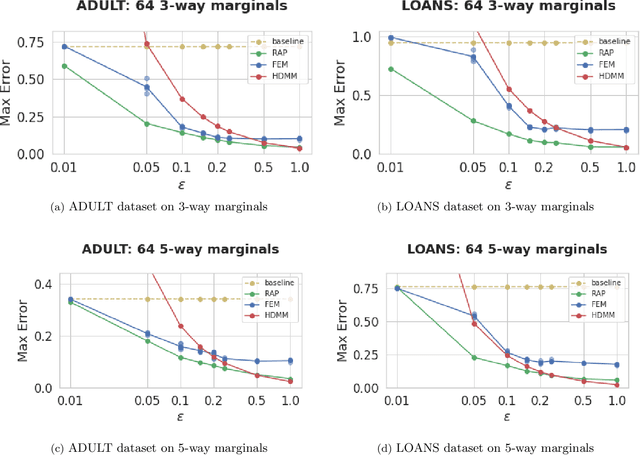
We propose, implement, and evaluate a new algorithm for releasing answers to very large numbers of statistical queries like $k$-way marginals, subject to differential privacy. Our algorithm makes adaptive use of a continuous relaxation of the Projection Mechanism, which answers queries on the private dataset using simple perturbation, and then attempts to find the synthetic dataset that most closely matches the noisy answers. We use a continuous relaxation of the synthetic dataset domain which makes the projection loss differentiable, and allows us to use efficient ML optimization techniques and tooling. Rather than answering all queries up front, we make judicious use of our privacy budget by iteratively and adaptively finding queries for which our (relaxed) synthetic data has high error, and then repeating the projection. We perform extensive experimental evaluations across a range of parameters and datasets, and find that our method outperforms existing algorithms in many cases, especially when the privacy budget is small or the query class is large.

Lexicographically Fair Learning: Algorithms and Generalization

We extend the notion of minimax fairness in supervised learning problems to its natural conclusion: lexicographic minimax fairness (or lexifairness for short). Informally, given a collection of demographic groups of interest, minimax fairness asks that the error of the group with the highest error be minimized. Lexifairness goes further and asks that amongst all minimax fair solutions, the error of the group with the second highest error should be minimized, and amongst all of those solutions, the error of the group with the third highest error should be minimized, and so on. Despite its naturalness, correctly defining lexifairness is considerably more subtle than minimax fairness, because of inherent sensitivity to approximation error. We give a notion of approximate lexifairness that avoids this issue, and then derive oracle-efficient algorithms for finding approximately lexifair solutions in a very general setting. When the underlying empirical risk minimization problem absent fairness constraints is convex (as it is, for example, with linear and logistic regression), our algorithms are provably efficient even in the worst case. Finally, we show generalization bounds -- approximate lexifairness on the training sample implies approximate lexifairness on the true distribution with high probability. Our ability to prove generalization bounds depends on our choosing definitions that avoid the instability of naive definitions.

Online Multivalid Learning: Means, Moments, and Prediction Intervals

We present a general, efficient technique for providing contextual predictions that are "multivalid" in various senses, against an online sequence of adversarially chosen examples $(x,y)$. This means that the resulting estimates correctly predict various statistics of the labels $y$ not just marginally -- as averaged over the sequence of examples -- but also conditionally on $x \in G$ for any $G$ belonging to an arbitrary intersecting collection of groups $\mathcal{G}$. We provide three instantiations of this framework. The first is mean prediction, which corresponds to an online algorithm satisfying the notion of multicalibration from Hebert-Johnson et al. The second is variance and higher moment prediction, which corresponds to an online algorithm satisfying the notion of mean-conditioned moment multicalibration from Jung et al. Finally, we define a new notion of prediction interval multivalidity, and give an algorithm for finding prediction intervals which satisfy it. Because our algorithms handle adversarially chosen examples, they can equally well be used to predict statistics of the residuals of arbitrary point prediction methods, giving rise to very general techniques for quantifying the uncertainty of predictions of black box algorithms, even in an online adversarial setting. When instantiated for prediction intervals, this solves a similar problem as conformal prediction, but in an adversarial environment and with multivalidity guarantees stronger than simple marginal coverage guarantees.

Convergent Algorithms for (Relaxed) Minimax Fairness

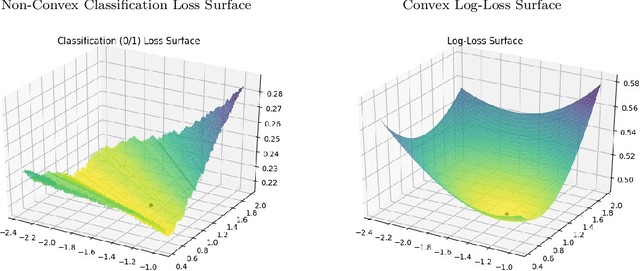
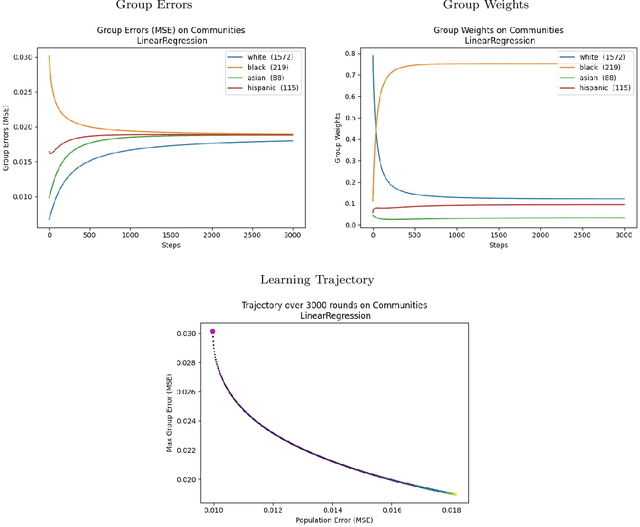
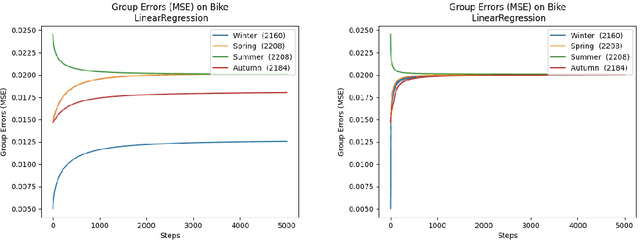
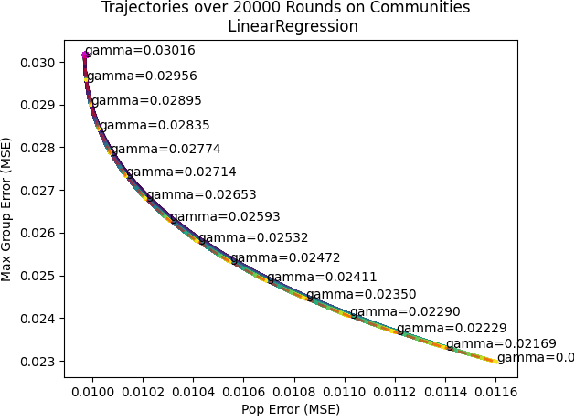
We consider a recently introduced framework in which fairness is measured by worst-case outcomes across groups, rather than by the more standard $\textit{difference}$ between group outcomes. In this framework we provide provably convergent $\textit{oracle-efficient}$ learning algorithms (or equivalently, reductions to non-fair learning) for $\textit{minimax group fairness}$. Here the goal is that of minimizing the maximum loss across all groups, rather than equalizing group losses. Our algorithms apply to both regression and classification settings and support both overall error and false positive or false negative rates as the fairness measure of interest. They also support relaxations of the fairness constraints, thus permitting study of the tradeoff between overall accuracy and minimax fairness. We compare the experimental behavior and performance of our algorithms across a variety of fairness-sensitive data sets and show cases in which minimax fairness is strictly and strongly preferable to equal outcome notions, in the sense that equal outcomes can only be obtained by artificially inflating the harm inflicted on some groups compared to what they suffer under the minimax solution.