Variance-Aware Sparse Linear Bandits

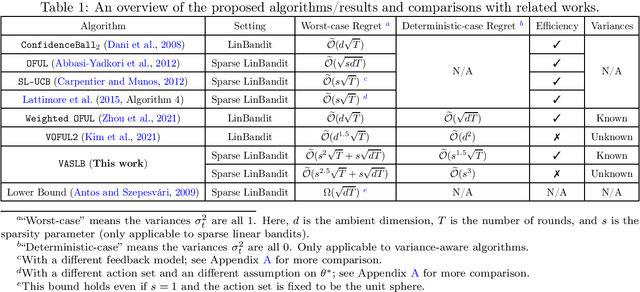
It is well-known that the worst-case minimax regret for sparse linear bandits is $\widetilde{\Theta}\left(\sqrt{dT}\right)$ where $d$ is the ambient dimension and $T$ is the number of time steps (ignoring the dependency on sparsity). On the other hand, in the benign setting where there is no noise and the action set is the unit sphere, one can use divide-and-conquer to achieve an $\widetilde{\mathcal O}(1)$ regret, which is (nearly) independent of $d$ and $T$. In this paper, we present the first variance-aware regret guarantee for sparse linear bandits: $\widetilde{\mathcal O}\left(\sqrt{d\sum_{t=1}^T \sigma_t^2} + 1\right)$, where $\sigma_t^2$ is the variance of the noise at the $t$-th time step. This bound naturally interpolates the regret bounds for the worst-case constant-variance regime ($\sigma_t = \Omega(1)$) and the benign deterministic regimes ($\sigma_t = 0$). To achieve this variance-aware regret guarantee, we develop a general framework that converts any variance-aware linear bandit algorithm to a variance-aware algorithm for sparse linear bandits in a ``black-box'' manner. Specifically, we take two recent algorithms as black boxes to illustrate that the claimed bounds indeed hold, where the first algorithm can handle unknown-variance cases and the second one is more efficient.