The planted matching problem: Sharp threshold and infinite-order phase transition
Paper and Code
Mar 17, 2021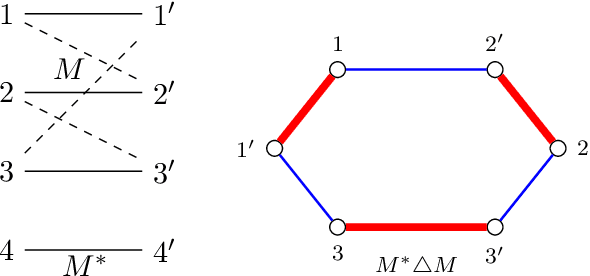
We study the problem of reconstructing a perfect matching $M^*$ hidden in a randomly weighted $n\times n$ bipartite graph. The edge set includes every node pair in $M^*$ and each of the $n(n-1)$ node pairs not in $M^*$ independently with probability $d/n$. The weight of each edge $e$ is independently drawn from the distribution $\mathcal{P}$ if $e \in M^*$ and from $\mathcal{Q}$ if $e \notin M^*$. We show that if $\sqrt{d} B(\mathcal{P},\mathcal{Q}) \le 1$, where $B(\mathcal{P},\mathcal{Q})$ stands for the Bhattacharyya coefficient, the reconstruction error (average fraction of misclassified edges) of the maximum likelihood estimator of $M^*$ converges to $0$ as $n\to \infty$. Conversely, if $\sqrt{d} B(\mathcal{P},\mathcal{Q}) \ge 1+\epsilon$ for an arbitrarily small constant $\epsilon>0$, the reconstruction error for any estimator is shown to be bounded away from $0$ under both the sparse and dense model, resolving the conjecture in [Moharrami et al. 2019, Semerjian et al. 2020]. Furthermore, in the special case of complete exponentially weighted graph with $d=n$, $\mathcal{P}=\exp(\lambda)$, and $\mathcal{Q}=\exp(1/n)$, for which the sharp threshold simplifies to $\lambda=4$, we prove that when $\lambda \le 4-\epsilon$, the optimal reconstruction error is $\exp\left( - \Theta(1/\sqrt{\epsilon}) \right)$, confirming the conjectured infinite-order phase transition in [Semerjian et al. 2020].
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge