Properly learning decision trees in almost polynomial time
Paper and Code
Sep 01, 2021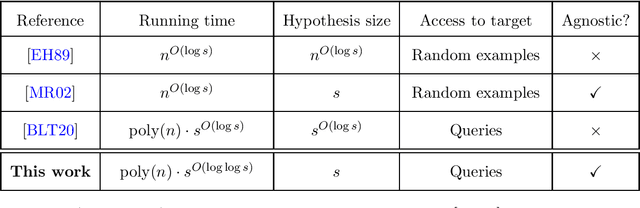


We give an $n^{O(\log\log n)}$-time membership query algorithm for properly and agnostically learning decision trees under the uniform distribution over $\{\pm 1\}^n$. Even in the realizable setting, the previous fastest runtime was $n^{O(\log n)}$, a consequence of a classic algorithm of Ehrenfeucht and Haussler. Our algorithm shares similarities with practical heuristics for learning decision trees, which we augment with additional ideas to circumvent known lower bounds against these heuristics. To analyze our algorithm, we prove a new structural result for decision trees that strengthens a theorem of O'Donnell, Saks, Schramm, and Servedio. While the OSSS theorem says that every decision tree has an influential variable, we show how every decision tree can be "pruned" so that every variable in the resulting tree is influential.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge