Poisson Matrix Completion
Paper and Code
Mar 25, 2015
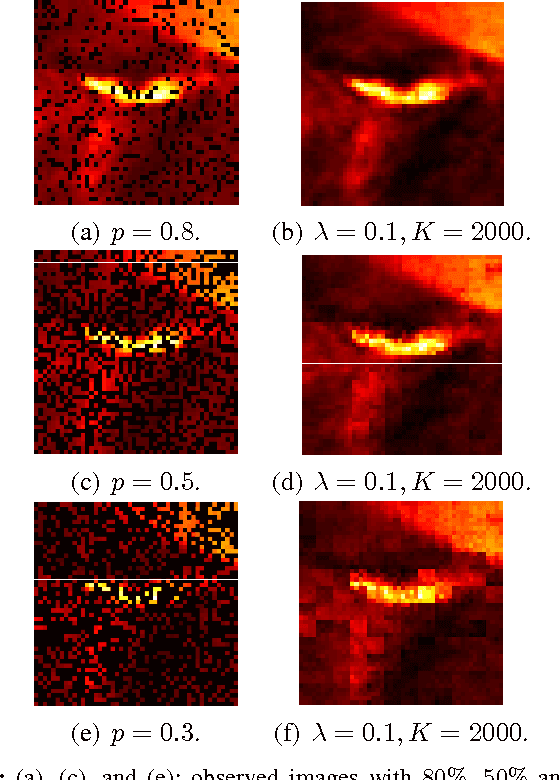
We extend the theory of matrix completion to the case where we make Poisson observations for a subset of entries of a low-rank matrix. We consider the (now) usual matrix recovery formulation through maximum likelihood with proper constraints on the matrix $M$, and establish theoretical upper and lower bounds on the recovery error. Our bounds are nearly optimal up to a factor on the order of $\mathcal{O}(\log(d_1 d_2))$. These bounds are obtained by adapting the arguments used for one-bit matrix completion \cite{davenport20121} (although these two problems are different in nature) and the adaptation requires new techniques exploiting properties of the Poisson likelihood function and tackling the difficulties posed by the locally sub-Gaussian characteristic of the Poisson distribution. Our results highlight a few important distinctions of Poisson matrix completion compared to the prior work in matrix completion including having to impose a minimum signal-to-noise requirement on each observed entry. We also develop an efficient iterative algorithm and demonstrate its good performance in recovering solar flare images.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge