LordNet: Learning to Solve Parametric Partial Differential Equations without Simulated Data

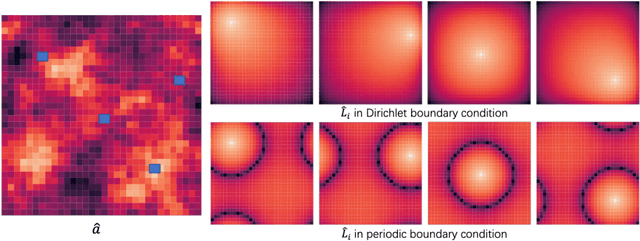
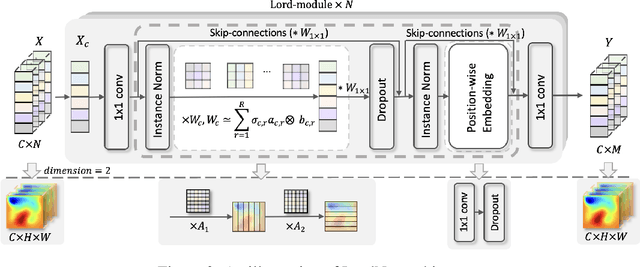
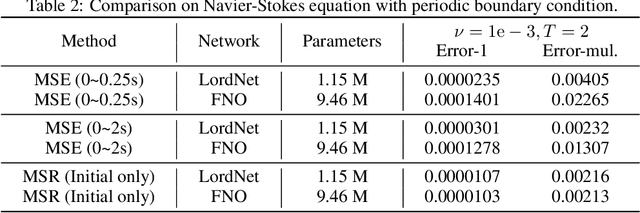
Neural operators, as a powerful approximation to the non-linear operators between infinite-dimensional function spaces, have proved to be promising in accelerating the solution of partial differential equations (PDE). However, it requires a large amount of simulated data which can be costly to collect, resulting in a chicken-egg dilemma and limiting its usage in solving PDEs. To jump out of the dilemma, we propose a general data-free paradigm where the neural network directly learns physics from the mean squared residual (MSR) loss constructed by the discretized PDE. We investigate the physical information in the MSR loss and identify the challenge that the neural network must have the capacity to model the long range entanglements in the spatial domain of the PDE, whose patterns vary in different PDEs. Therefore, we propose the low-rank decomposition network (LordNet) which is tunable and also efficient to model various entanglements. Specifically, LordNet learns a low-rank approximation to the global entanglements with simple fully connected layers, which extracts the dominant pattern with reduced computational cost. The experiments on solving Poisson's equation and Navier-Stokes equation demonstrate that the physical constraints by the MSR loss can lead to better accuracy and generalization ability of the neural network. In addition, LordNet outperforms other modern neural network architectures in both PDEs with the fewest parameters and the fastest inference speed. For Navier-Stokes equation, the learned operator is over 50 times faster than the finite difference solution with the same computational resources.