Linear Systems can be Hard to Learn

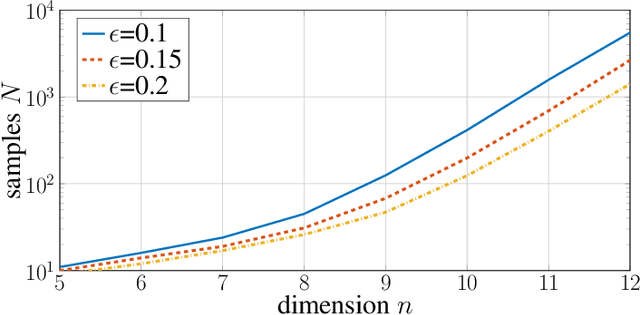
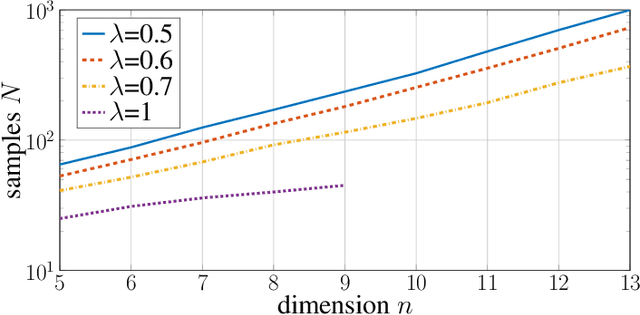
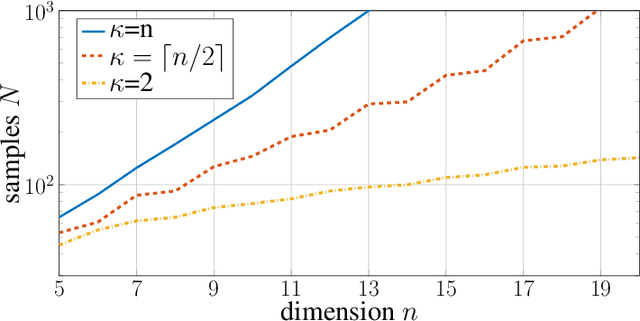
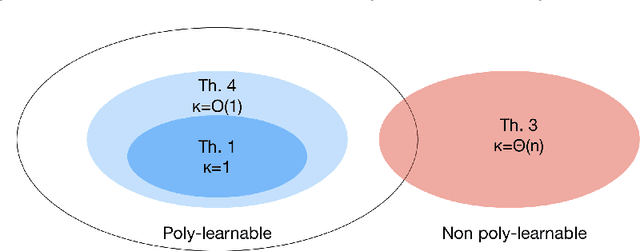
In this paper, we investigate when system identification is statistically easy or hard, in the finite sample regime. Statistically easy to learn linear system classes have sample complexity that is polynomial with the system dimension. Most prior research in the finite sample regime falls in this category, focusing on systems that are directly excited by process noise. Statistically hard to learn linear system classes have worst-case sample complexity that is at least exponential with the system dimension, regardless of the identification algorithm. Using tools from minimax theory, we show that classes of linear systems can be hard to learn. Such classes include, for example, under-actuated or under-excited systems with weak coupling among the states. Having classified some systems as easy or hard to learn, a natural question arises as to what system properties fundamentally affect the hardness of system identifiability. Towards this direction, we characterize how the controllability index of linear systems affects the sample complexity of identification. More specifically, we show that the sample complexity of robustly controllable linear systems is upper bounded by an exponential function of the controllability index. This implies that identification is easy for classes of linear systems with small controllability index and potentially hard if the controllability index is large. Our analysis is based on recent statistical tools for finite sample analysis of system identification as well as a novel lower bound that relates controllability index with the least singular value of the controllability Gramian.