Hierarchical community detection by recursive bi-partitioning

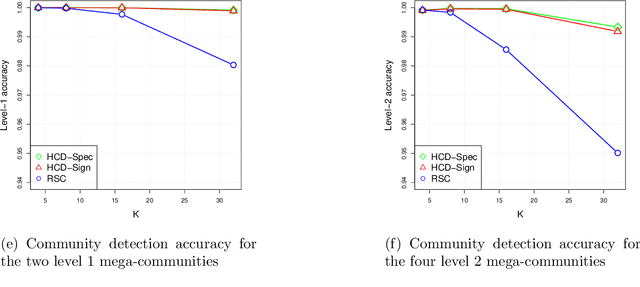
The problem of community detection in networks is usually formulated as finding a single partition of the network into some "correct" number of communities. We argue that it is more interpretable and in some regimes more accurate to construct a hierarchical tree of communities instead. This can be done with a simple top-down recursive bi-partitioning algorithm, starting with a single community and separating the nodes into two communities by spectral clustering repeatedly, until a stopping rule suggests there are no further communities. Such an algorithm is model-free, extremely fast, and requires no tuning other than selecting a stopping rule. We show that there are regimes where it outperforms $K$-way spectral clustering, and propose a natural model for analyzing the algorithm's theoretical performance, the binary tree stochastic block model. Under this model, we prove that the algorithm correctly recovers the entire community tree under relatively mild assumptions. We also apply the algorithm to a dataset of statistics papers to construct a hierarchical tree of statistical research communities.