Generative Subgraph Contrast for Self-Supervised Graph Representation Learning
Paper and Code
Jul 26, 2022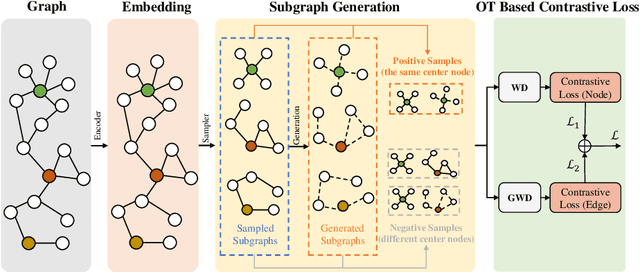
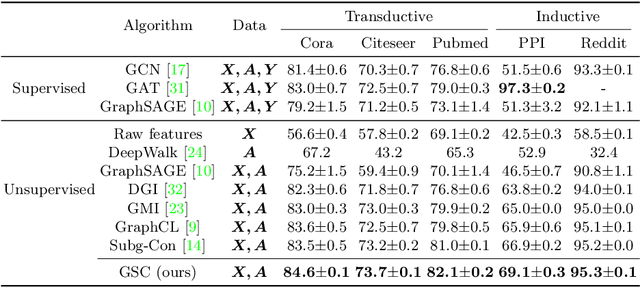
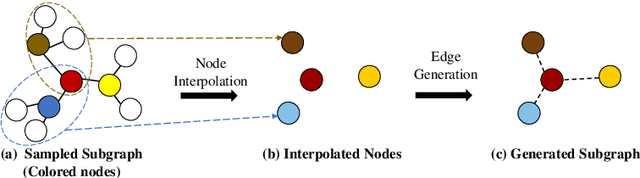

Contrastive learning has shown great promise in the field of graph representation learning. By manually constructing positive/negative samples, most graph contrastive learning methods rely on the vector inner product based similarity metric to distinguish the samples for graph representation. However, the handcrafted sample construction (e.g., the perturbation on the nodes or edges of the graph) may not effectively capture the intrinsic local structures of the graph. Also, the vector inner product based similarity metric cannot fully exploit the local structures of the graph to characterize the graph difference well. To this end, in this paper, we propose a novel adaptive subgraph generation based contrastive learning framework for efficient and robust self-supervised graph representation learning, and the optimal transport distance is utilized as the similarity metric between the subgraphs. It aims to generate contrastive samples by capturing the intrinsic structures of the graph and distinguish the samples based on the features and structures of subgraphs simultaneously. Specifically, for each center node, by adaptively learning relation weights to the nodes of the corresponding neighborhood, we first develop a network to generate the interpolated subgraph. We then construct the positive and negative pairs of subgraphs from the same and different nodes, respectively. Finally, we employ two types of optimal transport distances (i.e., Wasserstein distance and Gromov-Wasserstein distance) to construct the structured contrastive loss. Extensive node classification experiments on benchmark datasets verify the effectiveness of our graph contrastive learning method.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge