Generalization Properties of Decision Trees on Real-valued and Categorical Features
Paper and Code
Oct 18, 2022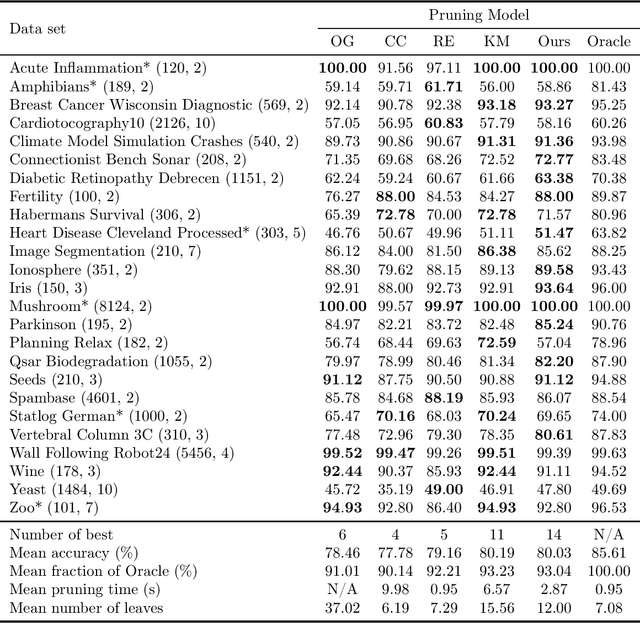

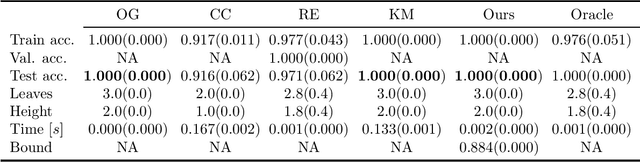
We revisit binary decision trees from the perspective of partitions of the data. We introduce the notion of partitioning function, and we relate it to the growth function and to the VC dimension. We consider three types of features: real-valued, categorical ordinal and categorical nominal, with different split rules for each. For each feature type, we upper bound the partitioning function of the class of decision stumps before extending the bounds to the class of general decision tree (of any fixed structure) using a recursive approach. Using these new results, we are able to find the exact VC dimension of decision stumps on examples of $\ell$ real-valued features, which is given by the largest integer $d$ such that $2\ell \ge \binom{d}{\lfloor\frac{d}{2}\rfloor}$. Furthermore, we show that the VC dimension of a binary tree structure with $L_T$ leaves on examples of $\ell$ real-valued features is in $O(L_T \log(L_T\ell))$. Finally, we elaborate a pruning algorithm based on these results that performs better than the cost-complexity and reduced-error pruning algorithms on a number of data sets, with the advantage that no cross-validation is required.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge