Coordinating the Motion of Labeled Discs with Optimality Guarantees under Extreme Density
Paper and Code
Jul 09, 2018
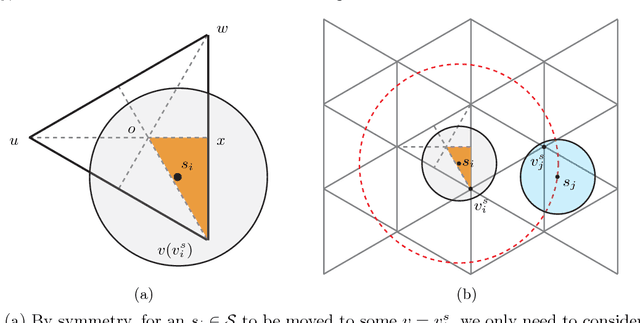
We push the limit in planning collision-free motions for routing uniform labeled discs in two dimensions. First, from a theoretical perspective, we show that the constant-factor time-optimal routing of labeled discs can be achieved using a polynomial-time algorithm with robot density over $50\%$ in the limit (i.e., over half of the workspace may be occupied by the discs). Second, from a more practical standpoint, we provide a high performance algorithm that computes near-optimal (e.g., $1.x$) solutions under the same density setting.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge