Estimation of the Mean Function of Functional Data via Deep Neural Networks

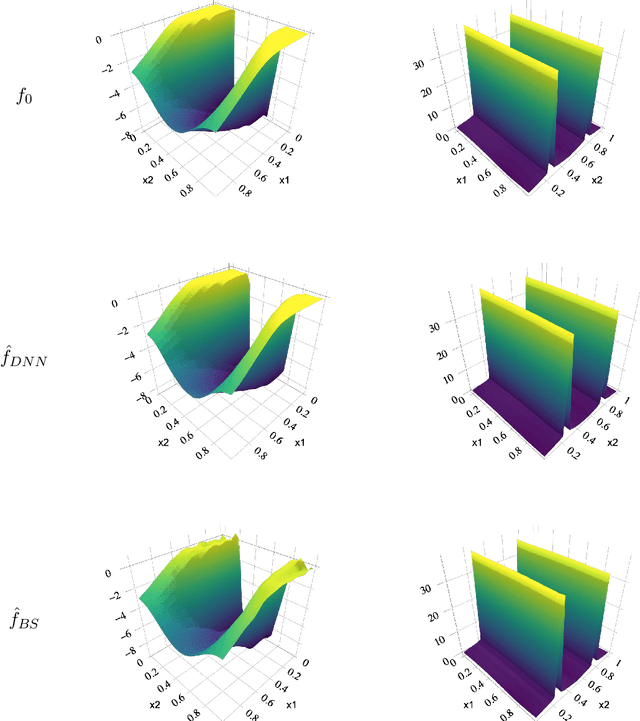
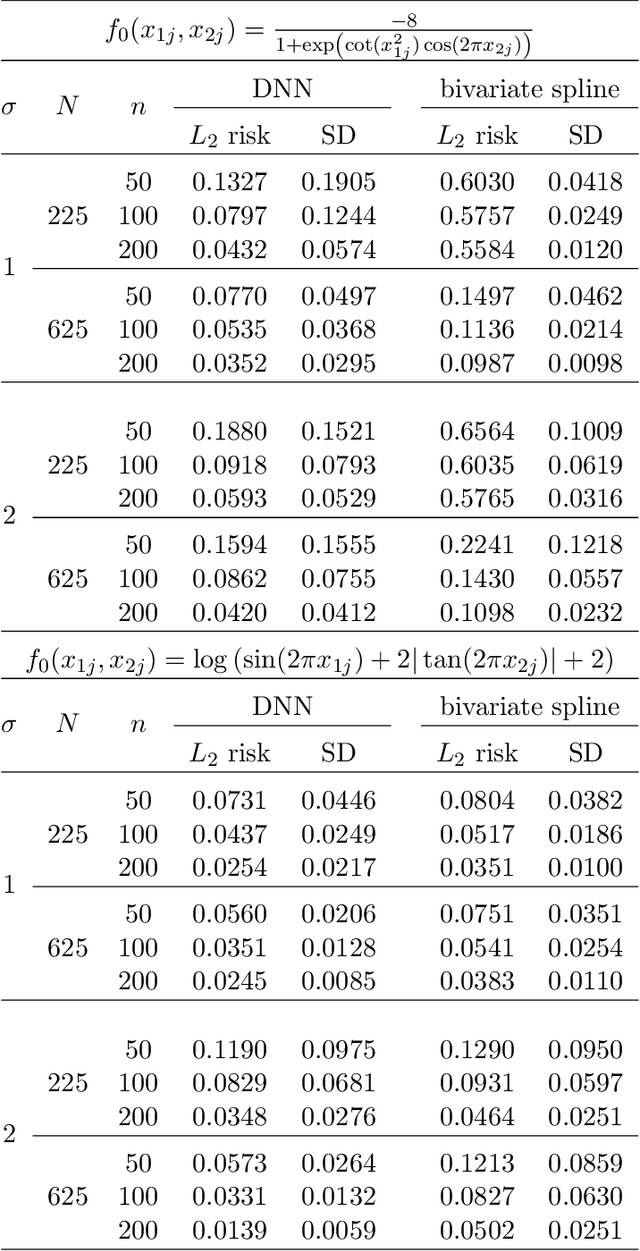
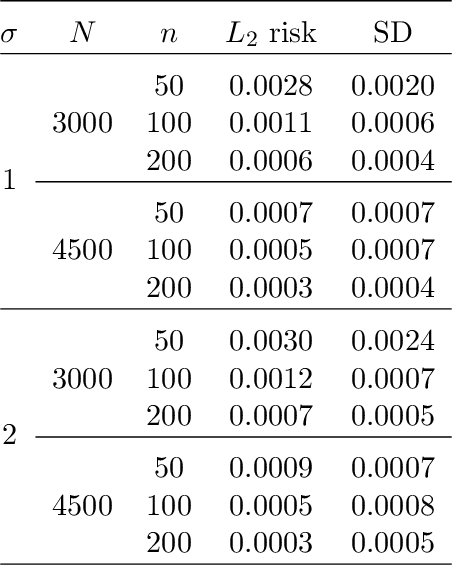
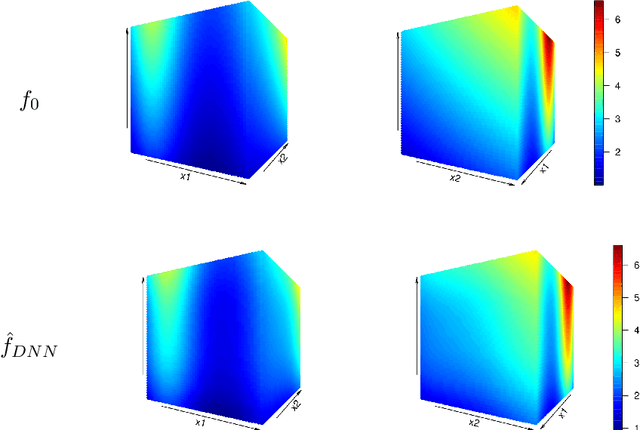
In this work, we propose a deep neural network method to perform nonparametric regression for functional data. The proposed estimators are based on sparsely connected deep neural networks with ReLU activation function. By properly choosing network architecture, our estimator achieves the optimal nonparametric convergence rate in empirical norm. Under certain circumstances such as trigonometric polynomial kernel and a sufficiently large sampling frequency, the convergence rate is even faster than root-$n$ rate. Through Monte Carlo simulation studies we examine the finite-sample performance of the proposed method. Finally, the proposed method is applied to analyze positron emission tomography images of patients with Alzheimer disease obtained from the Alzheimer Disease Neuroimaging Initiative database.

On Deep Instrumental Variables Estimate

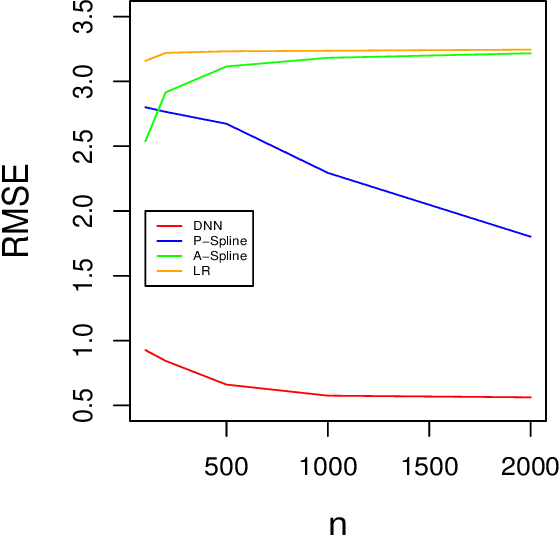
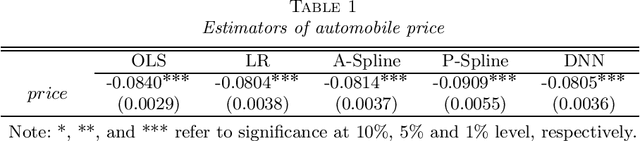
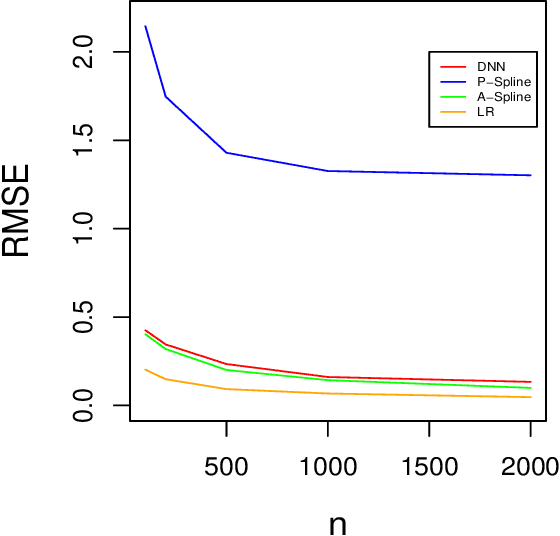
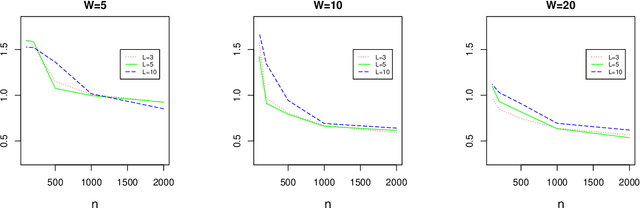
The endogeneity issue is fundamentally important as many empirical applications may suffer from the omission of explanatory variables, measurement error, or simultaneous causality. Recently, \cite{hllt17} propose a "Deep Instrumental Variable (IV)" framework based on deep neural networks to address endogeneity, demonstrating superior performances than existing approaches. The aim of this paper is to theoretically understand the empirical success of the Deep IV. Specifically, we consider a two-stage estimator using deep neural networks in the linear instrumental variables model. By imposing a latent structural assumption on the reduced form equation between endogenous variables and instrumental variables, the first-stage estimator can automatically capture this latent structure and converge to the optimal instruments at the minimax optimal rate, which is free of the dimension of instrumental variables and thus mitigates the curse of dimensionality. Additionally, in comparison with classical methods, due to the faster convergence rate of the first-stage estimator, the second-stage estimator has {a smaller (second order) estimation error} and requires a weaker condition on the smoothness of the optimal instruments. Given that the depth and width of the employed deep neural network are well chosen, we further show that the second-stage estimator achieves the semiparametric efficiency bound. Simulation studies on synthetic data and application to automobile market data confirm our theory.

Sharp Rate of Convergence for Deep Neural Network Classifiers under the Teacher-Student Setting

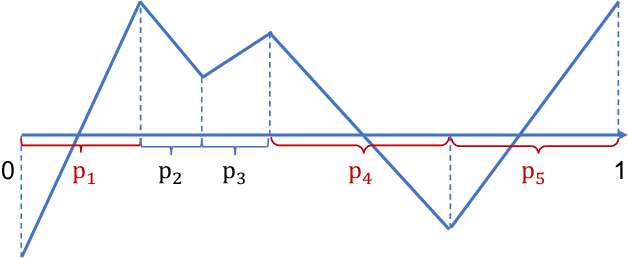
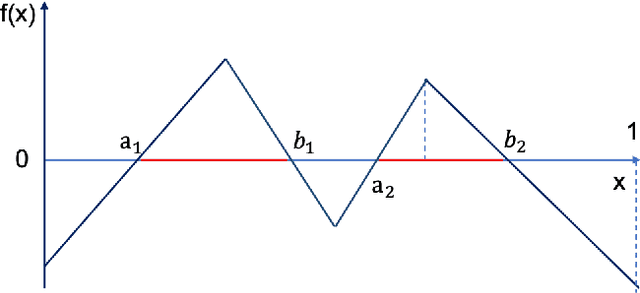
Classifiers built with neural networks handle large-scale high dimensional data, such as facial images from computer vision, extremely well while traditional statistical methods often fail miserably. In this paper, we attempt to understand this empirical success in high dimensional classification by deriving the convergence rates of excess risk. In particular, a teacher-student framework is proposed that assumes the Bayes classifier to be expressed as ReLU neural networks. In this setup, we obtain a sharp rate of convergence, i.e., $\tilde{O}_d(n^{-2/3})$, for classifiers trained using either 0-1 loss or hinge loss. This rate can be further improved to $\tilde{O}_d(n^{-1})$ when the data distribution is separable. Here, $n$ denotes the sample size. An interesting observation is that the data dimension only contributes to the $\log(n)$ term in the above rates. This may provide one theoretical explanation for the empirical successes of deep neural networks in high dimensional classification, particularly for structured data.

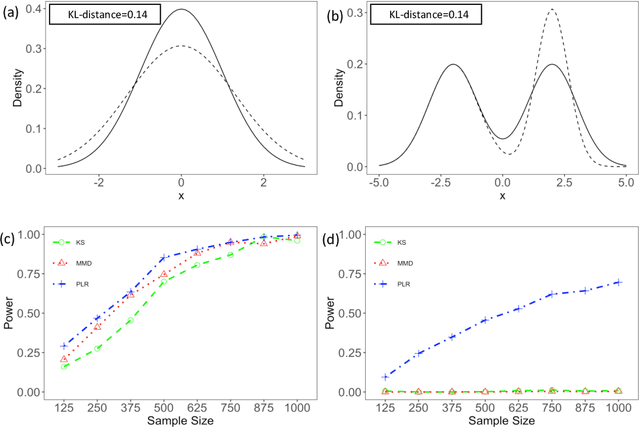
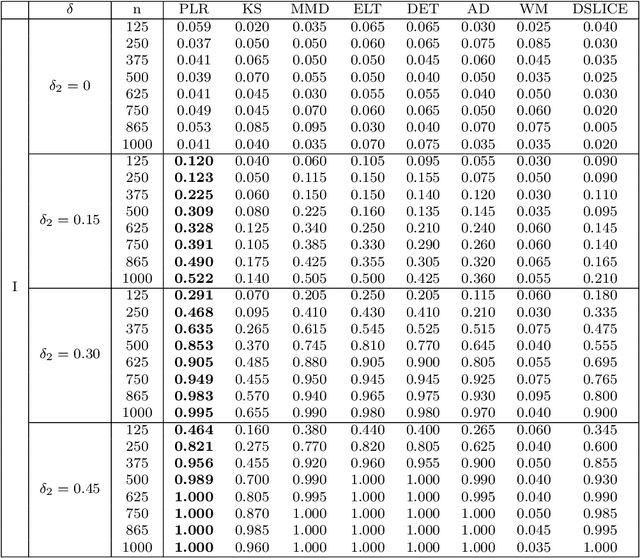
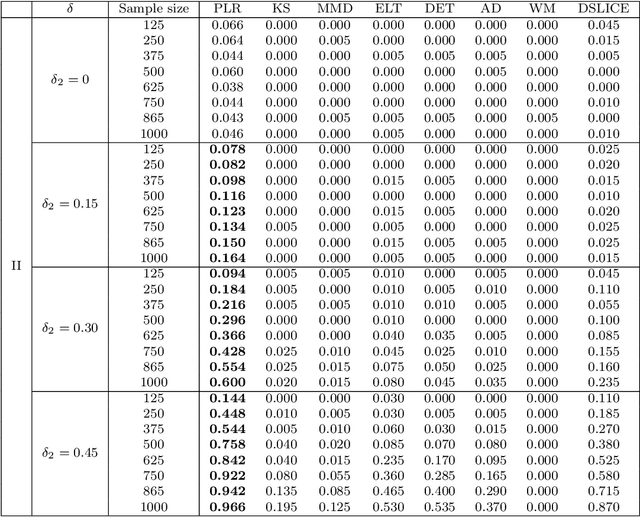
Minimax Nonparametric Two-sample Test

We consider the problem of comparing probability densities between two groups. To model the complex pattern of the underlying densities, we formulate the problem as a nonparametric density hypothesis testing problem. The major difficulty is that conventional tests may fail to distinguish the alternative from the null hypothesis under the controlled type I error. In this paper, we model log-transformed densities in a tensor product reproducing kernel Hilbert space (RKHS) and propose a probabilistic decomposition of this space. Under such a decomposition, we quantify the difference of the densities between two groups by the component norm in the probabilistic decomposition. Based on the Bernstein width, a sharp minimax lower bound of the distinguishable rate is established for the nonparametric two-sample test. We then propose a penalized likelihood ratio (PLR) test possessing the Wilks' phenomenon with an asymptotically Chi-square distributed test statistic and achieving the established minimax testing rate. Simulations and real applications demonstrate that the proposed test outperforms the conventional approaches under various scenarios.

Optimal Nonparametric Inference via Deep Neural Network

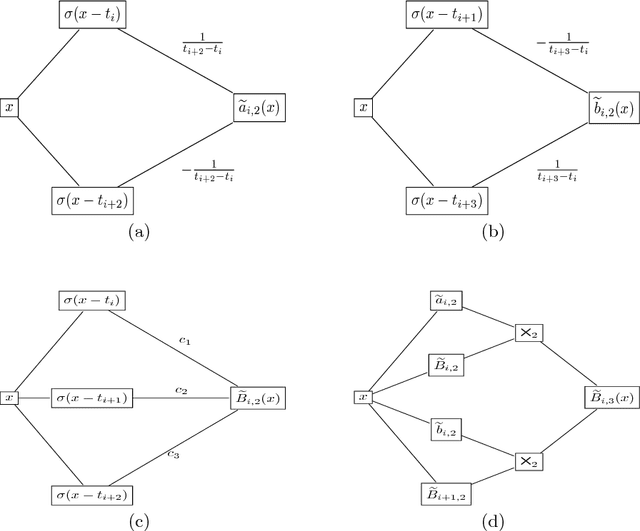
Deep neural network is a state-of-art method in modern science and technology. Much statistical literature have been devoted to understanding its performance in nonparametric estimation, whereas the results are suboptimal due to a redundant logarithmic sacrifice. In this paper, we show that such log-factors are not necessary. We derive upper bounds for the $L^2$ minimax risk in nonparametric estimation. Sufficient conditions on network architectures are provided such that the upper bounds become optimal (without log-sacrifice). Our proof relies on an explicitly constructed network estimator based on tensor product B-splines. We also derive asymptotic distributions for the constructed network and a relating hypothesis testing procedure. The testing procedure is further proven as minimax optimal under suitable network architectures.

Optimal Nonparametric Inference under Quantization

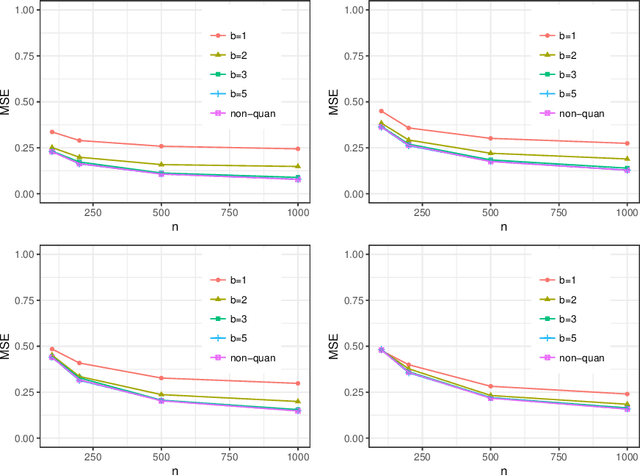
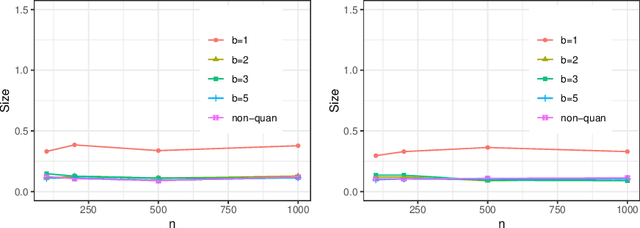
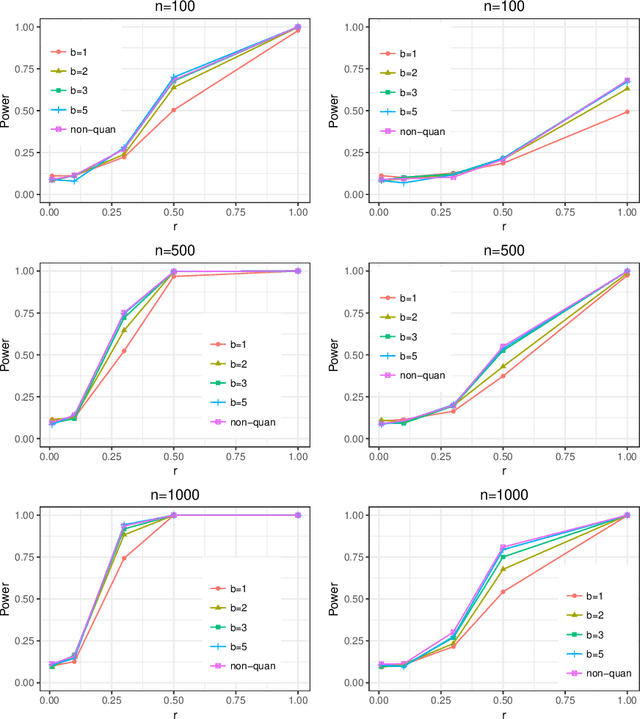
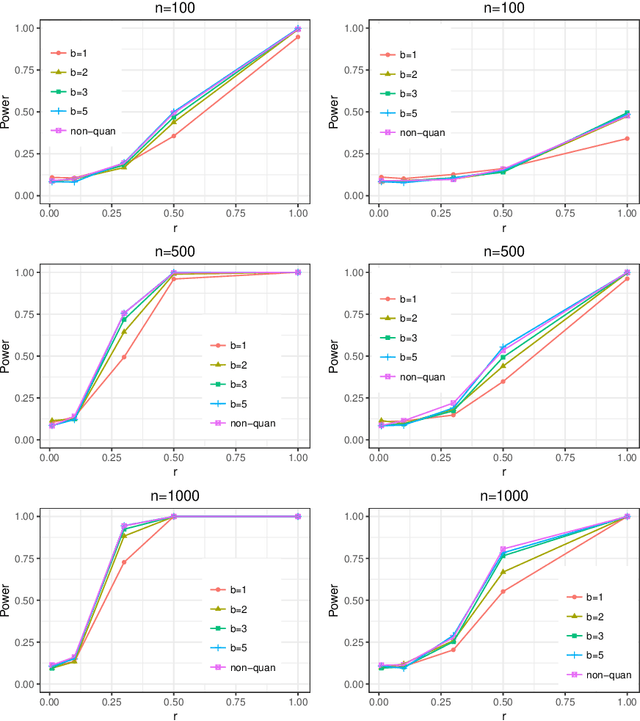
Statistical inference based on lossy or incomplete samples is of fundamental importance in research areas such as signal/image processing, medical image storage, remote sensing, signal transmission. In this paper, we propose a nonparametric testing procedure based on quantized samples. In contrast to the classic nonparametric approach, our method lives on a coarse grid of sample information and are simple-to-use. Under mild technical conditions, we establish the asymptotic properties of the proposed procedures including asymptotic null distribution of the quantization test statistic as well as its minimax power optimality. Concrete quantizers are constructed for achieving the minimax optimality in practical use. Simulation results and a real data analysis are provided to demonstrate the validity and effectiveness of the proposed test. Our work bridges the classical nonparametric inference to modern lossy data setting.

How Many Machines Can We Use in Parallel Computing for Kernel Ridge Regression?

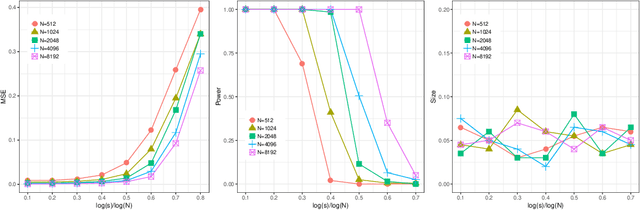
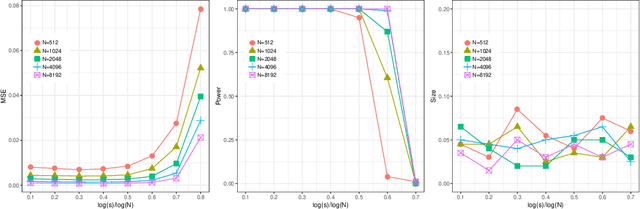
This paper attempts to solve a basic problem in distributed statistical inference: how many machines can we use in parallel computing? In kernel ridge regression, we address this question in two important settings: nonparametric estimation and hypothesis testing. Specifically, we find a range for the number of machines under which optimal estimation/testing is achievable. The employed empirical processes method provides a unified framework, that allows us to handle various regression problems (such as thin-plate splines and nonparametric additive regression) under different settings (such as univariate, multivariate and diverging-dimensional designs). It is worth noting that the upper bounds of the number of machines are proven to be un-improvable (up to a logarithmic factor) in two important cases: smoothing spline regression and Gaussian RKHS regression. Our theoretical findings are backed by thorough numerical studies.

A likelihood-ratio type test for stochastic block models with bounded degrees

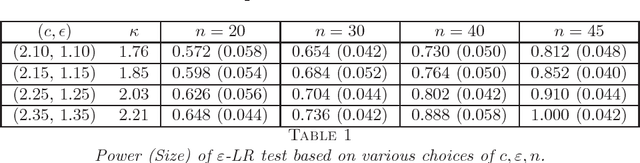
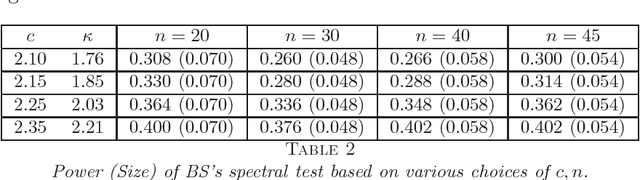
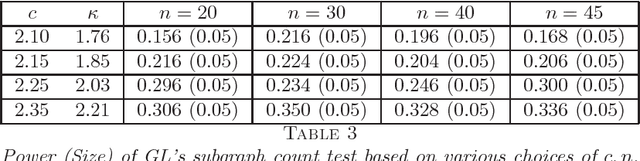
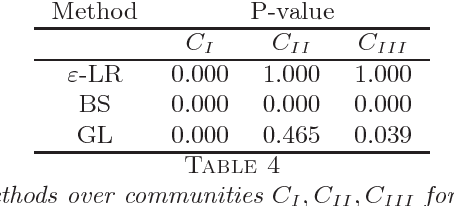
A fundamental problem in network data analysis is to test Erd\"{o}s-R\'{e}nyi model $\mathcal{G}\left(n,\frac{a+b}{2n}\right)$ versus a bisection stochastic block model $\mathcal{G}\left(n,\frac{a}{n},\frac{b}{n}\right)$, where $a,b>0$ are constants that represent the expected degrees of the graphs and $n$ denotes the number of nodes. This problem serves as the foundation of many other problems such as testing-based methods for determining the number of communities (\cite{BS16,L16}) and community detection (\cite{MS16}). Existing work has been focusing on growing-degree regime $a,b\to\infty$ (\cite{BS16,L16,MS16,BM17,B18,GL17a,GL17b}) while leaving the bounded-degree regime untreated. In this paper, we propose a likelihood-ratio (LR) type procedure based on regularization to test stochastic block models with bounded degrees. We derive the limit distributions as power Poisson laws under both null and alternative hypotheses, based on which the limit power of the test is carefully analyzed. We also examine a Monte-Carlo method that partly resolves the computational cost issue. The proposed procedures are examined by both simulated and real-world data. The proof depends on a contiguity theory developed by Janson \cite{J95}.

Nonparametric Testing under Random Projection

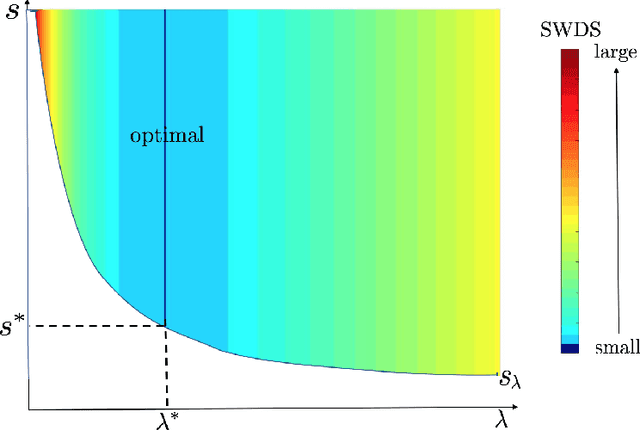
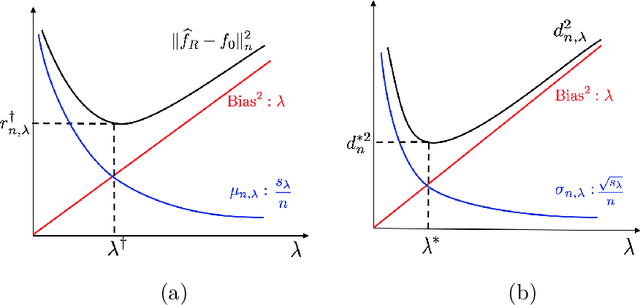
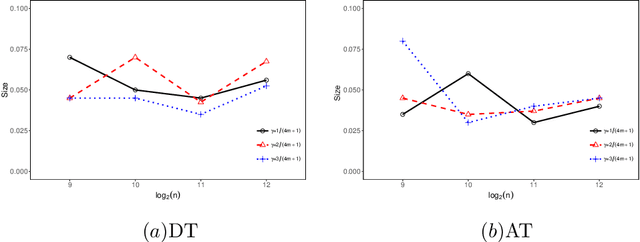
A common challenge in nonparametric inference is its high computational complexity when data volume is large. In this paper, we develop computationally efficient nonparametric testing by employing a random projection strategy. In the specific kernel ridge regression setup, a simple distance-based test statistic is proposed. Notably, we derive the minimum number of random projections that is sufficient for achieving testing optimality in terms of the minimax rate. An adaptive testing procedure is further established without prior knowledge of regularity. One technical contribution is to establish upper bounds for a range of tail sums of empirical kernel eigenvalues. Simulations and real data analysis are conducted to support our theory.

Optimal tuning for divide-and-conquer kernel ridge regression with massive data

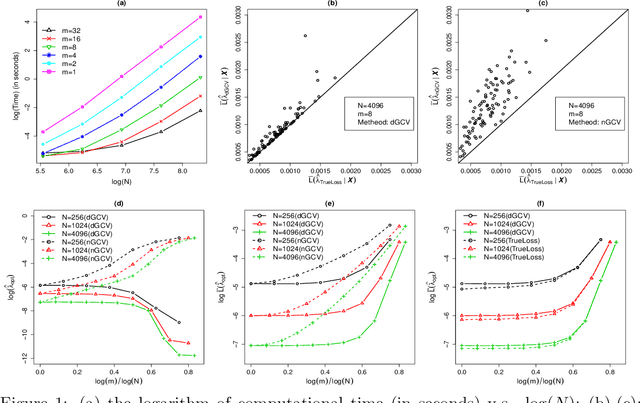
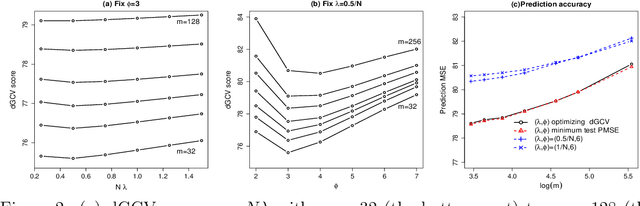
We propose a first data-driven tuning procedure for divide-and-conquer kernel ridge regression (Zhang et al., 2015). While the proposed criterion is computationally scalable for massive data sets, it is also shown to be asymptotically optimal under mild conditions. The effectiveness of our method is illustrated by extensive simulations and an application to Million Song Dataset.