Learning in the Machine: the Symmetries of the Deep Learning Channel

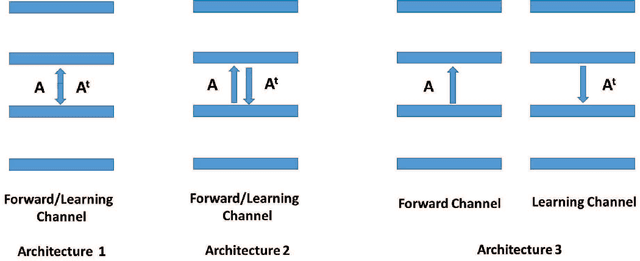
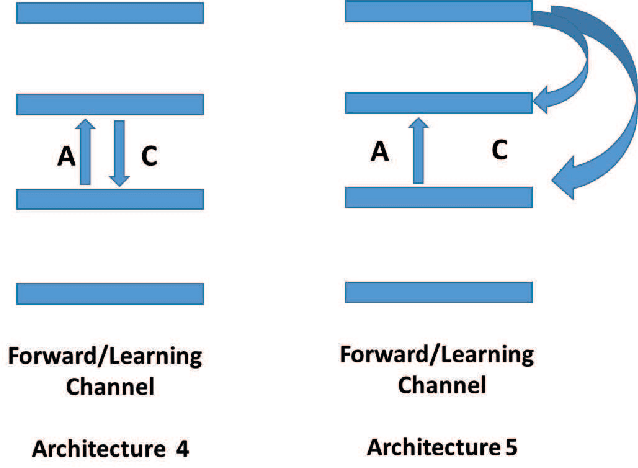
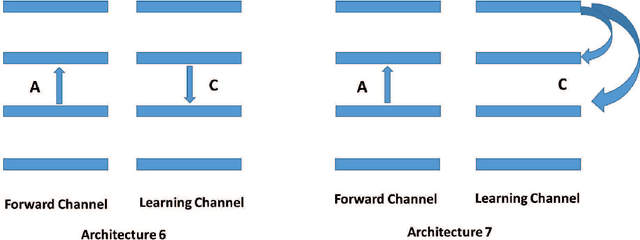
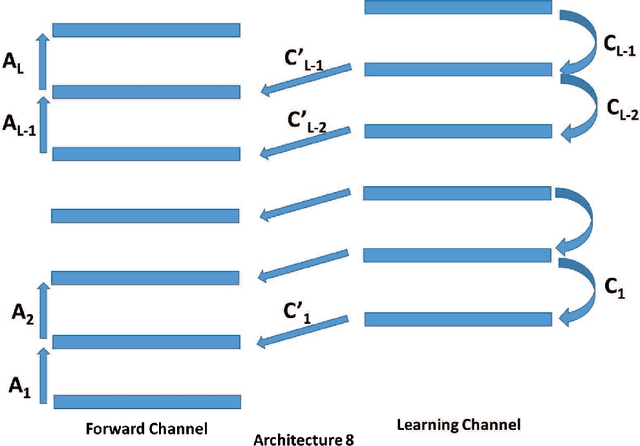
In a physical neural system, learning rules must be local both in space and time. In order for learning to occur, non-local information must be communicated to the deep synapses through a communication channel, the deep learning channel. We identify several possible architectures for this learning channel (Bidirectional, Conjoined, Twin, Distinct) and six symmetry challenges: 1) symmetry of architectures; 2) symmetry of weights; 3) symmetry of neurons; 4) symmetry of derivatives; 5) symmetry of processing; and 6) symmetry of learning rules. Random backpropagation (RBP) addresses the second and third symmetry, and some of its variations, such as skipped RBP (SRBP) address the first and the fourth symmetry. Here we address the last two desirable symmetries showing through simulations that they can be achieved and that the learning channel is particularly robust to symmetry variations. Specifically, random backpropagation and its variations can be performed with the same non-linear neurons used in the main input-output forward channel, and the connections in the learning channel can be adapted using the same algorithm used in the forward channel, removing the need for any specialized hardware in the learning channel. Finally, we provide mathematical results in simple cases showing that the learning equations in the forward and backward channels converge to fixed points, for almost any initial conditions. In symmetric architectures, if the weights in both channels are small at initialization, adaptation in both channels leads to weights that are essentially symmetric during and after learning. Biological connections are discussed.

Learning in the Machine: Random Backpropagation and the Deep Learning Channel

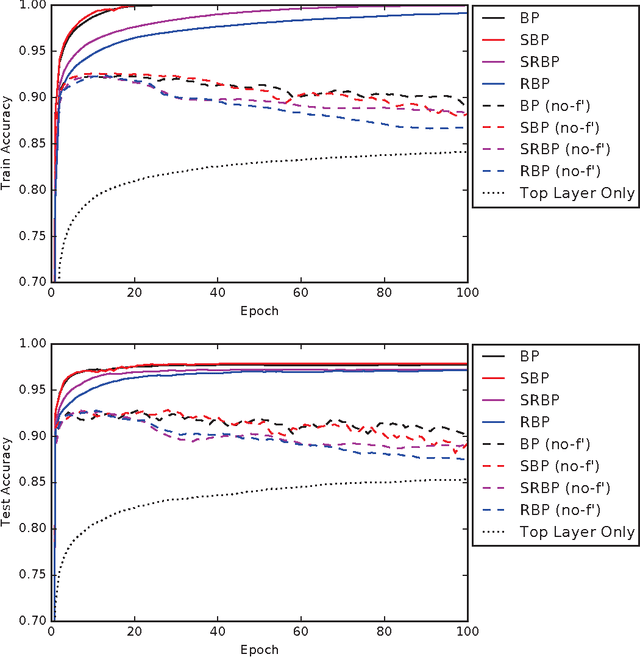
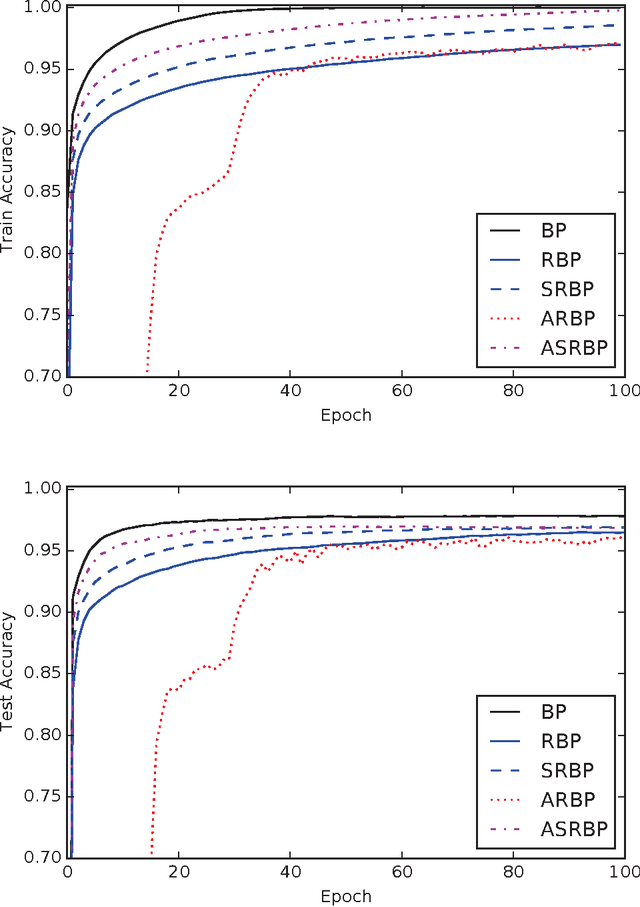
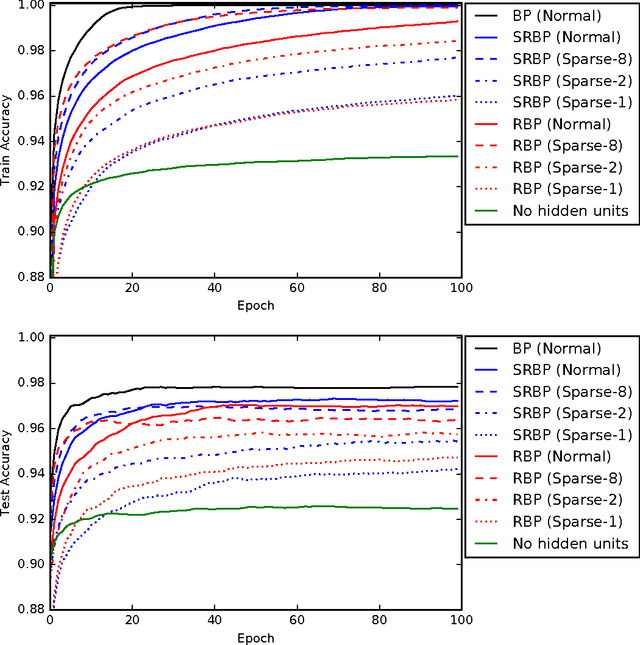
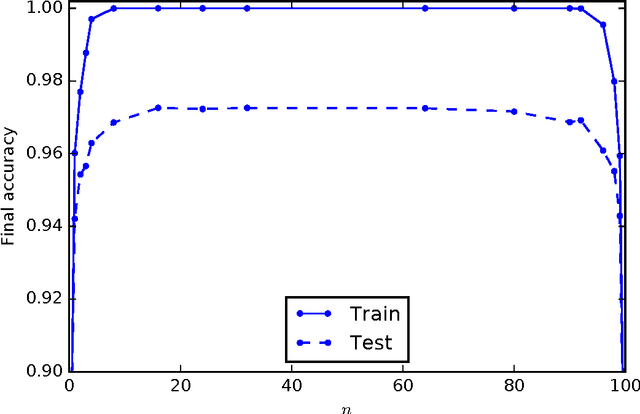
Random backpropagation (RBP) is a variant of the backpropagation algorithm for training neural networks, where the transpose of the forward matrices are replaced by fixed random matrices in the calculation of the weight updates. It is remarkable both because of its effectiveness, in spite of using random matrices to communicate error information, and because it completely removes the taxing requirement of maintaining symmetric weights in a physical neural system. To better understand random backpropagation, we first connect it to the notions of local learning and learning channels. Through this connection, we derive several alternatives to RBP, including skipped RBP (SRPB), adaptive RBP (ARBP), sparse RBP, and their combinations (e.g. ASRBP) and analyze their computational complexity. We then study their behavior through simulations using the MNIST and CIFAR-10 bechnmark datasets. These simulations show that most of these variants work robustly, almost as well as backpropagation, and that multiplication by the derivatives of the activation functions is important. As a follow-up, we study also the low-end of the number of bits required to communicate error information over the learning channel. We then provide partial intuitive explanations for some of the remarkable properties of RBP and its variations. Finally, we prove several mathematical results, including the convergence to fixed points of linear chains of arbitrary length, the convergence to fixed points of linear autoencoders with decorrelated data, the long-term existence of solutions for linear systems with a single hidden layer and convergence in special cases, and the convergence to fixed points of non-linear chains, when the derivative of the activation functions is included.

Complex-Valued Autoencoders

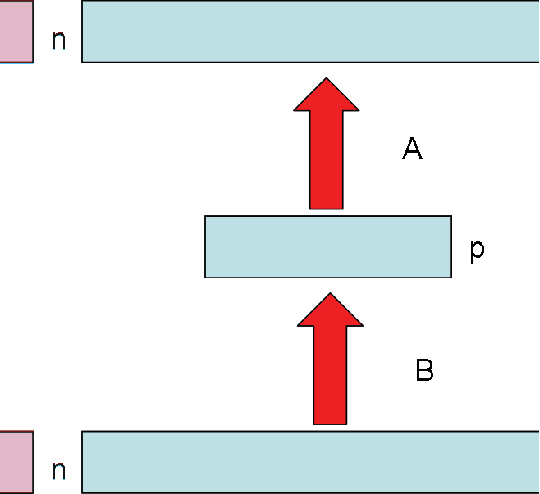
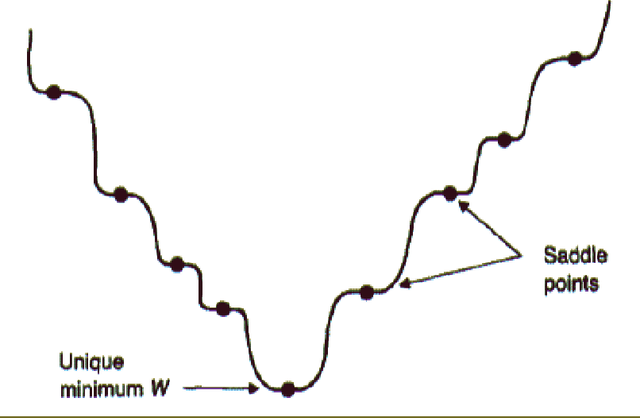
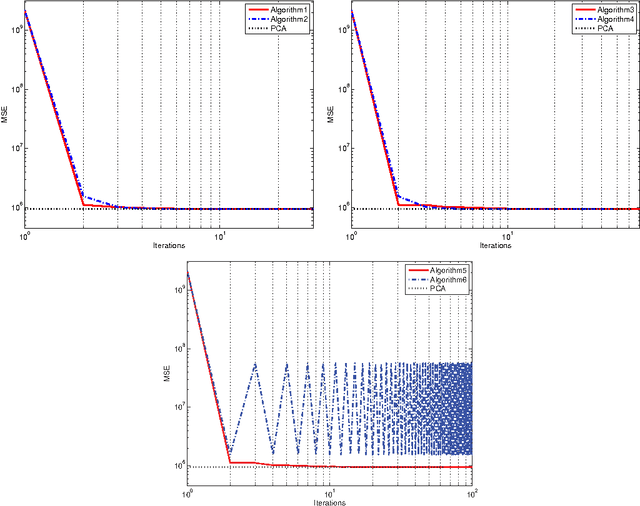
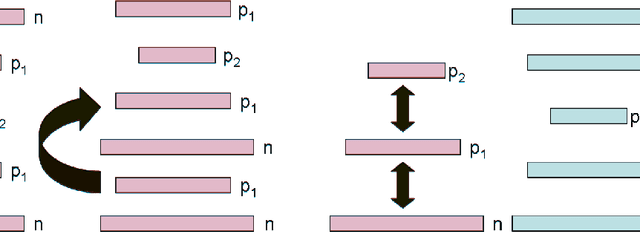
Autoencoders are unsupervised machine learning circuits whose learning goal is to minimize a distortion measure between inputs and outputs. Linear autoencoders can be defined over any field and only real-valued linear autoencoder have been studied so far. Here we study complex-valued linear autoencoders where the components of the training vectors and adjustable matrices are defined over the complex field with the $L_2$ norm. We provide simpler and more general proofs that unify the real-valued and complex-valued cases, showing that in both cases the landscape of the error function is invariant under certain groups of transformations. The landscape has no local minima, a family of global minima associated with Principal Component Analysis, and many families of saddle points associated with orthogonal projections onto sub-space spanned by sub-optimal subsets of eigenvectors of the covariance matrix. The theory yields several iterative, convergent, learning algorithms, a clear understanding of the generalization properties of the trained autoencoders, and can equally be applied to the hetero-associative case when external targets are provided. Partial results on deep architecture as well as the differential geometry of autoencoders are also presented. The general framework described here is useful to classify autoencoders and identify general common properties that ought to be investigated for each class, illuminating some of the connections between information theory, unsupervised learning, clustering, Hebbian learning, and autoencoders.