Minimal Sample Subspace Learning: Theory and Algorithms

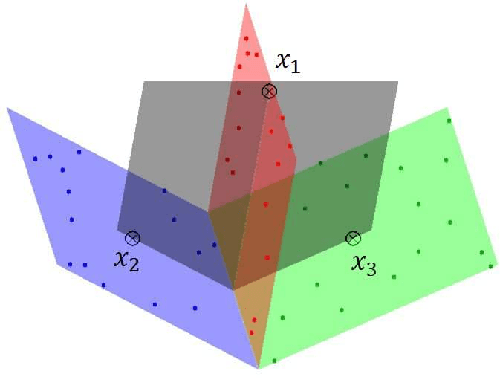
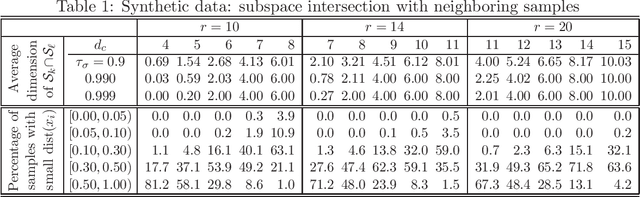
Subspace segmentation or subspace learning is a challenging and complicated task in machine learning. This paper builds a primary frame and solid theoretical bases for the minimal subspace segmentation (MSS) of finite samples. Existence and conditional uniqueness of MSS are discussed with conditions generally satisfied in applications. Utilizing weak prior information of MSS, the minimality inspection of segments is further simplified to the prior detection of partitions. The MSS problem is then modeled as a computable optimization problem via self-expressiveness of samples. A closed form of representation matrices is first given for the self-expressiveness, and the connection of diagonal blocks is then addressed. The MSS model uses a rank restriction on the sum of segment ranks. Theoretically, it can retrieve the minimal sample subspaces that could be heavily intersected. The optimization problem is solved via a basic manifold conjugate gradient algorithm, alternative optimization and hybrid optimization, taking into account of solving both the primal MSS problem and its pseudo-dual problem. The MSS model is further modified for handling noisy data, and solved by an ADMM algorithm. The reported experiments show the strong ability of the MSS method on retrieving minimal sample subspaces that are heavily intersected.

Principal Boundary on Riemannian Manifolds

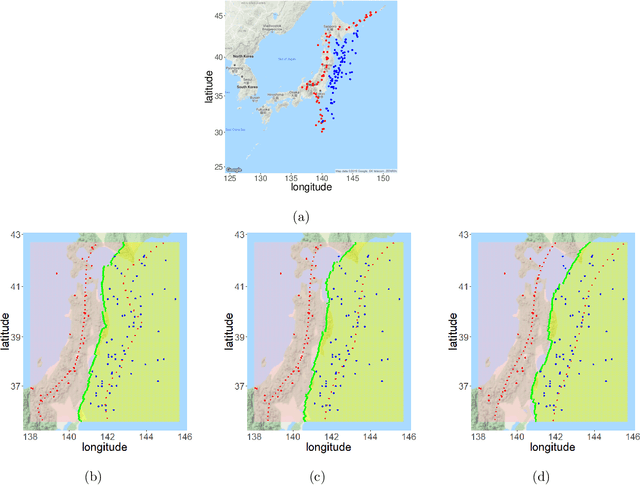
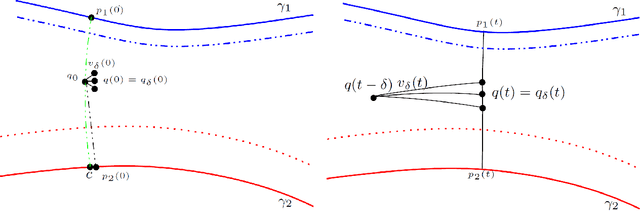
We revisit the classification problem and focus on nonlinear methods for classification on manifolds. For multivariate datasets lying on an embedded nonlinear Riemannian manifold within the higher-dimensional space, our aim is to acquire a classification boundary between the classes with labels. Motivated by the principal flow [Panaretos, Pham and Yao, 2014], a curve that moves along a path of the maximum variation of the data, we introduce the principal boundary. From the classification perspective, the principal boundary is defined as an optimal curve that moves in between the principal flows traced out from two classes of the data, and at any point on the boundary, it maximizes the margin between the two classes. We estimate the boundary in quality with its direction supervised by the two principal flows. We show that the principal boundary yields the usual decision boundary found by the support vector machine, in the sense that locally, the two boundaries coincide. By means of examples, we illustrate how to find, use and interpret the principal boundary.

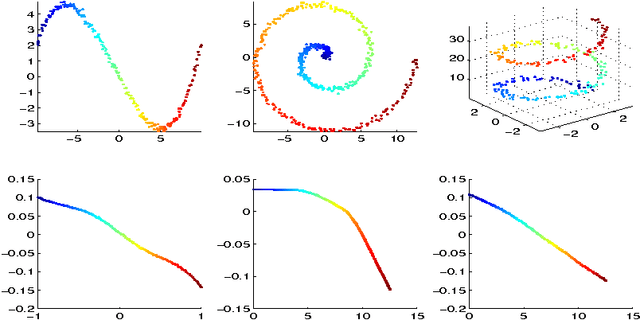
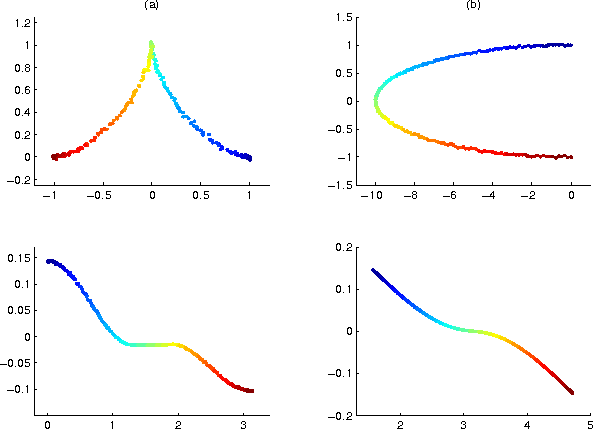
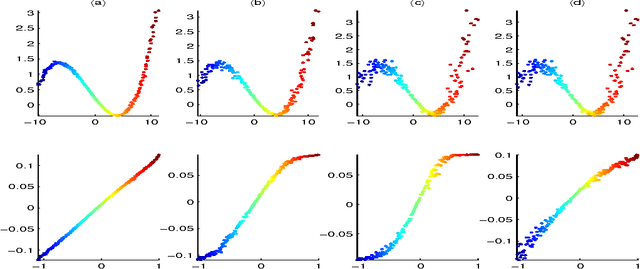
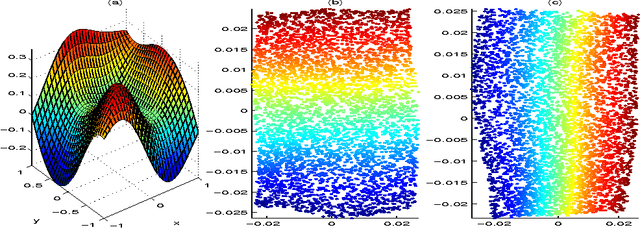
Principal Manifolds and Nonlinear Dimension Reduction via Local Tangent Space Alignment

Nonlinear manifold learning from unorganized data points is a very challenging unsupervised learning and data visualization problem with a great variety of applications. In this paper we present a new algorithm for manifold learning and nonlinear dimension reduction. Based on a set of unorganized data points sampled with noise from the manifold, we represent the local geometry of the manifold using tangent spaces learned by fitting an affine subspace in a neighborhood of each data point. Those tangent spaces are aligned to give the internal global coordinates of the data points with respect to the underlying manifold by way of a partial eigendecomposition of the neighborhood connection matrix. We present a careful error analysis of our algorithm and show that the reconstruction errors are of second-order accuracy. We illustrate our algorithm using curves and surfaces both in 2D/3D and higher dimensional Euclidean spaces, and 64-by-64 pixel face images with various pose and lighting conditions. We also address several theoretical and algorithmic issues for further research and improvements.