Zhenxun Zhuang
Adaptive Strategies in Non-convex Optimization
Jun 17, 2023



Abstract:An algorithm is said to be adaptive to a certain parameter (of the problem) if it does not need a priori knowledge of such a parameter but performs competitively to those that know it. This dissertation presents our work on adaptive algorithms in following scenarios: 1. In the stochastic optimization setting, we only receive stochastic gradients and the level of noise in evaluating them greatly affects the convergence rate. Tuning is typically required when without prior knowledge of the noise scale in order to achieve the optimal rate. Considering this, we designed and analyzed noise-adaptive algorithms that can automatically ensure (near)-optimal rates under different noise scales without knowing it. 2. In training deep neural networks, the scales of gradient magnitudes in each coordinate can scatter across a very wide range unless normalization techniques, like BatchNorm, are employed. In such situations, algorithms not addressing this problem of gradient scales can behave very poorly. To mitigate this, we formally established the advantage of scale-free algorithms that adapt to the gradient scales and presented its real benefits in empirical experiments. 3. Traditional analyses in non-convex optimization typically rely on the smoothness assumption. Yet, this condition does not capture the properties of some deep learning objective functions, including the ones involving Long Short-Term Memory networks and Transformers. Instead, they satisfy a much more relaxed condition, with potentially unbounded smoothness. Under this condition, we show that a generalized SignSGD algorithm can theoretically match the best-known convergence rates obtained by SGD with gradient clipping but does not need explicit clipping at all, and it can empirically match the performance of Adam and beat others. Moreover, it can also be made to automatically adapt to the unknown relaxed smoothness.
Robustness to Unbounded Smoothness of Generalized SignSGD
Aug 23, 2022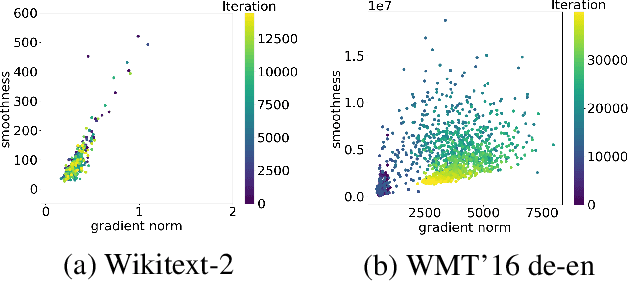
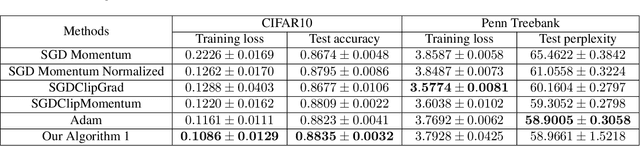
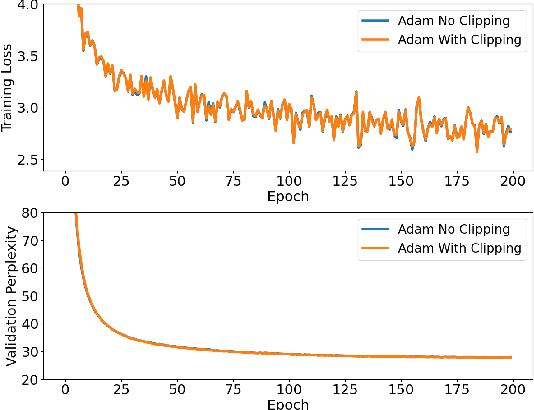

Abstract:Traditional analyses in non-convex optimization typically rely on the smoothness assumption, namely requiring the gradients to be Lipschitz. However, recent evidence shows that this smoothness condition does not capture the properties of some deep learning objective functions, including the ones involving Recurrent Neural Networks and LSTMs. Instead, they satisfy a much more relaxed condition, with potentially unbounded smoothness. Under this relaxed assumption, it has been theoretically and empirically shown that the gradient-clipped SGD has an advantage over the vanilla one. In this paper, we show that clipping is not indispensable for Adam-type algorithms in tackling such scenarios: we theoretically prove that a generalized SignSGD algorithm can obtain similar convergence rates as SGD with clipping but does not need explicit clipping at all. This family of algorithms on one end recovers SignSGD and on the other end closely resembles the popular Adam algorithm. Our analysis underlines the critical role that momentum plays in analyzing SignSGD-type and Adam-type algorithms: it not only reduces the effects of noise, thus removing the need for large mini-batch in previous analyses of SignSGD-type algorithms, but it also substantially reduces the effects of unbounded smoothness and gradient norms. We also compare these algorithms with popular optimizers on a set of deep learning tasks, observing that we can match the performance of Adam while beating the others.
A Communication-Efficient Distributed Gradient Clipping Algorithm for Training Deep Neural Networks
May 10, 2022
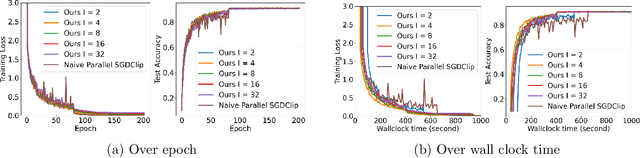
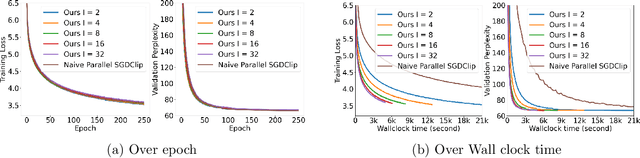
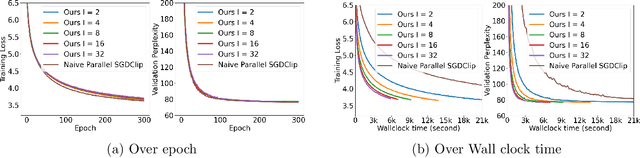
Abstract:In distributed training of deep neural networks or Federated Learning (FL), people usually run Stochastic Gradient Descent (SGD) or its variants on each machine and communicate with other machines periodically. However, SGD might converge slowly in training some deep neural networks (e.g., RNN, LSTM) because of the exploding gradient issue. Gradient clipping is usually employed to address this issue in the single machine setting, but exploring this technique in the FL setting is still in its infancy: it remains mysterious whether the gradient clipping scheme can take advantage of multiple machines to enjoy parallel speedup. The main technical difficulty lies in dealing with nonconvex loss function, non-Lipschitz continuous gradient, and skipping communication rounds simultaneously. In this paper, we explore a relaxed-smoothness assumption of the loss landscape which LSTM was shown to satisfy in previous works and design a communication-efficient gradient clipping algorithm. This algorithm can be run on multiple machines, where each machine employs a gradient clipping scheme and communicate with other machines after multiple steps of gradient-based updates. Our algorithm is proved to have $O\left(\frac{1}{N\epsilon^4}\right)$ iteration complexity for finding an $\epsilon$-stationary point, where $N$ is the number of machines. This indicates that our algorithm enjoys linear speedup. We prove this result by introducing novel analysis techniques of estimating truncated random variables, which we believe are of independent interest. Our experiments on several benchmark datasets and various scenarios demonstrate that our algorithm indeed exhibits fast convergence speed in practice and thus validates our theory.
Understanding AdamW through Proximal Methods and Scale-Freeness
Jan 31, 2022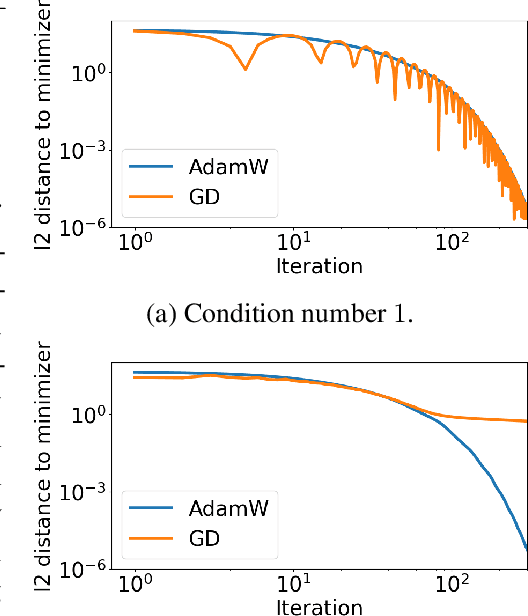
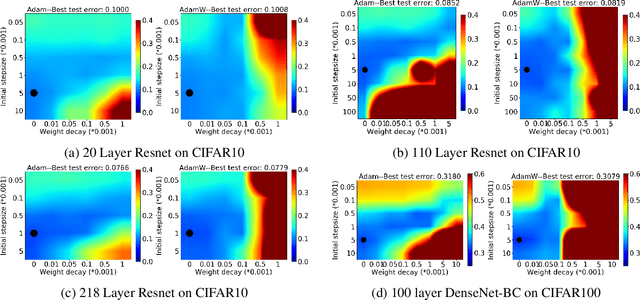
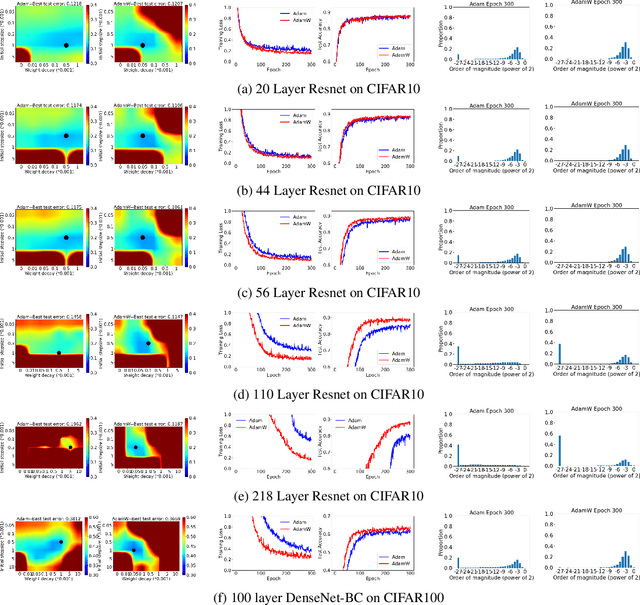
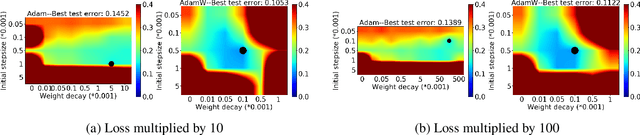
Abstract:Adam has been widely adopted for training deep neural networks due to less hyperparameter tuning and remarkable performance. To improve generalization, Adam is typically used in tandem with a squared $\ell_2$ regularizer (referred to as Adam-$\ell_2$). However, even better performance can be obtained with AdamW, which decouples the gradient of the regularizer from the update rule of Adam-$\ell_2$. Yet, we are still lacking a complete explanation of the advantages of AdamW. In this paper, we tackle this question from both an optimization and an empirical point of view. First, we show how to re-interpret AdamW as an approximation of a proximal gradient method, which takes advantage of the closed-form proximal mapping of the regularizer instead of only utilizing its gradient information as in Adam-$\ell_2$. Next, we consider the property of "scale-freeness" enjoyed by AdamW and by its proximal counterpart: their updates are invariant to component-wise rescaling of the gradients. We provide empirical evidence across a wide range of deep learning experiments showing a correlation between the problems in which AdamW exhibits an advantage over Adam-$\ell_2$ and the degree to which we expect the gradients of the network to exhibit multiple scales, thus motivating the hypothesis that the advantage of AdamW could be due to the scale-free updates.
Exponential Step Sizes for Non-Convex Optimization
Feb 12, 2020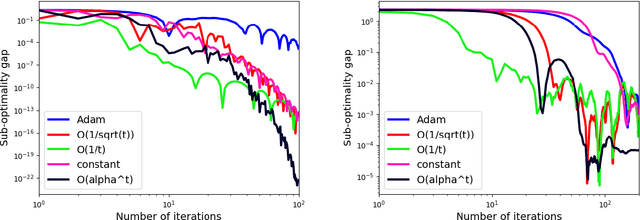
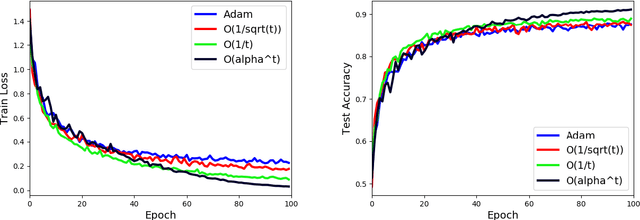
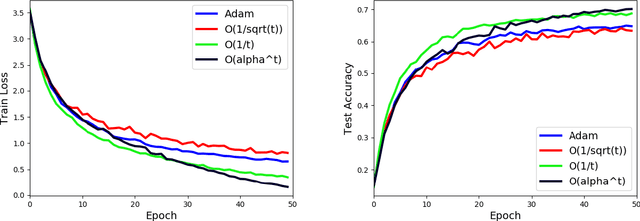
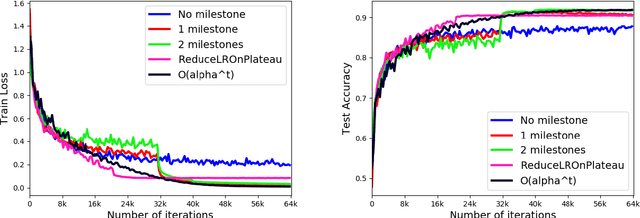
Abstract:Stochastic Gradient Descent (SGD) is a popular tool in large scale optimization of machine learning objective functions. However, the performance is greatly variable, depending on the choice of the step sizes. In this paper, we introduce the exponential step sizes for stochastic optimization of smooth non-convex functions which satisfy the Polyak-\L{}ojasiewicz (PL) condition. We show that, without any information on the level of noise over the stochastic gradients, these step sizes guarantee a convergence rate for the last iterate that automatically interpolates between a linear rate (in the noisy-free case) and a $O(\frac{1}{T})$ rate (in the noisy case), up to poly-logarithmic factors. Moreover, if without the PL condition, the exponential step sizes still guarantee optimal convergence to a critical point, up to logarithmic factors. We also validate our theoretical results with empirical experiments on real-world datasets with deep learning architectures.
Online Meta-Learning on Non-convex Setting
Oct 22, 2019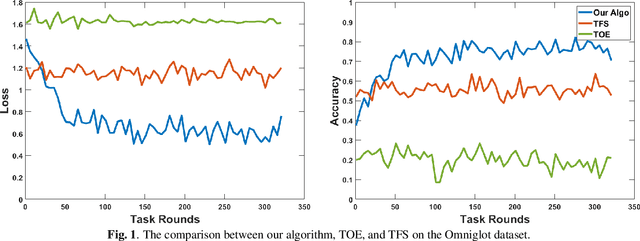
Abstract:The online meta-learning framework is designed for the continual lifelong learning setting. It bridges two fields: meta-learning which tries to extract prior knowledge from existing tasks for fast learning of future tasks, and online-learning which focuses on the sequential setting in which problems are revealed one by one. In this paper, we generalize the original framework from convex to non-convex setting, and introduce the local regret as the alternative performance measure. We then apply this framework to stochastic settings, and show theoretically that it enjoys a logarithmic local regret, and is robust to any hyperparameter initialization. The empirical test on a real-world task demonstrates its superiority compared with traditional methods.
Surrogate Losses for Online Learning of Stepsizes in Stochastic Non-Convex Optimization
Jan 25, 2019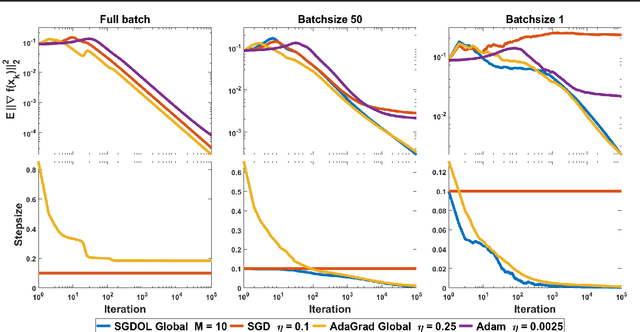
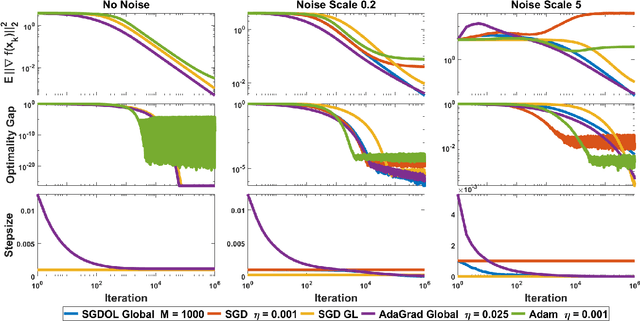
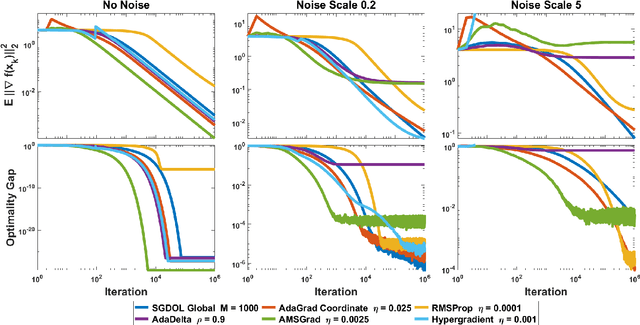
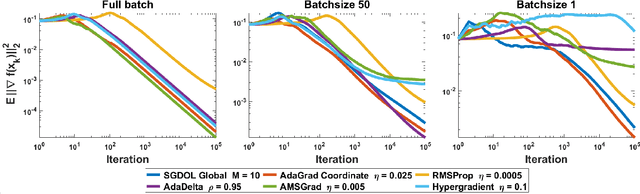
Abstract:Stochastic Gradient Descent (SGD) has played a central role in machine learning. However, it requires a carefully hand-picked stepsize for fast convergence, which is notoriously tedious and time-consuming to tune. Over the last several years, a plethora of adaptive gradient-based algorithms have emerged to ameliorate this problem. They have proved efficient in reducing the labor of tuning in practice, but many of them lack theoretic guarantees even in the convex setting. In this paper, we propose new surrogate losses to cast the problem of learning the optimal stepsizes for the stochastic optimization of a non-convex smooth objective function onto an online convex optimization problem. This allows the use of no-regret online algorithms to compute optimal stepsizes on the fly. In turn, this results in a SGD algorithm with self-tuned stepsizes that guarantees convergence rates that are automatically adaptive to the level of noise.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge