Conditional Diffusion Guidance under Hard Constraint: A Stochastic Analysis Approach

We study conditional generation in diffusion models under hard constraints, where generated samples must satisfy prescribed events with probability one. Such constraints arise naturally in safety-critical applications and in rare-event simulation, where soft or reward-based guidance methods offer no guarantee of constraint satisfaction. Building on a probabilistic interpretation of diffusion models, we develop a principled conditional diffusion guidance framework based on Doob's h-transform, martingale representation and quadratic variation process. Specifically, the resulting guided dynamics augment a pretrained diffusion with an explicit drift correction involving the logarithmic gradient of a conditioning function, without modifying the pretrained score network. Leveraging martingale and quadratic-variation identities, we propose two novel off-policy learning algorithms based on a martingale loss and a martingale-covariation loss to estimate h and its gradient using only trajectories from the pretrained model. We provide non-asymptotic guarantees for the resulting conditional sampler in both total variation and Wasserstein distances, explicitly characterizing the impact of score approximation and guidance estimation errors. Numerical experiments demonstrate the effectiveness of the proposed methods in enforcing hard constraints and generating rare-event samples.

Diffusion Generative Models Meet Compressed Sensing, with Applications to Image Data and Financial Time Series

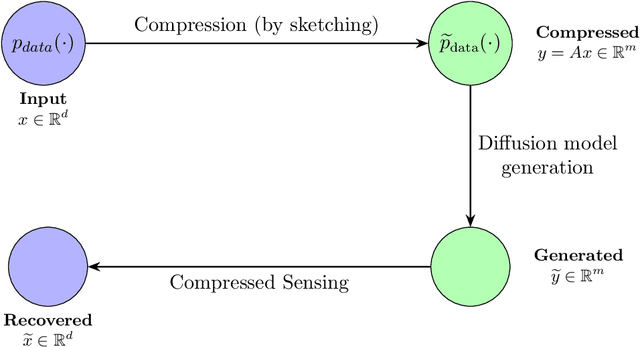
This paper develops dimension reduction techniques for accelerating diffusion model inference in the context of synthetic data generation. The idea is to integrate compressed sensing into diffusion models: (i) compress the data into a latent space, (ii) train a diffusion model in the latent space, and (iii) apply a compressed sensing algorithm to the samples generated in the latent space, facilitating the efficiency of both model training and inference. Under suitable sparsity assumptions on data, the proposed algorithm is proved to enjoy faster convergence by combining diffusion model inference with sparse recovery. As a byproduct, we obtain an optimal value for the latent space dimension. We also conduct numerical experiments on a range of datasets, including image data (handwritten digits, medical images, and climate data) and financial time series for stress testing.