Theoretical Analysis on how Learning Rate Warmup Accelerates Convergence

Learning rate warmup is a popular and practical technique in training large-scale deep neural networks. Despite the huge success in practice, the theoretical advantages of this strategy of gradually increasing the learning rate at the beginning of the training process have not been fully understood. To resolve this gap between theory and practice, we first propose a novel family of generalized smoothness assumptions, and validate its applicability both theoretically and empirically. Under the novel smoothness assumption, we study the convergence properties of gradient descent (GD) in both deterministic and stochastic settings. It is shown that learning rate warmup consistently accelerates GD, and GD with warmup can converge at most $\Theta(T)$ times faster than with a non-increasing learning rate schedule in some specific cases, providing insights into the benefits of this strategy from an optimization theory perspective.

SOREL: A Stochastic Algorithm for Spectral Risks Minimization

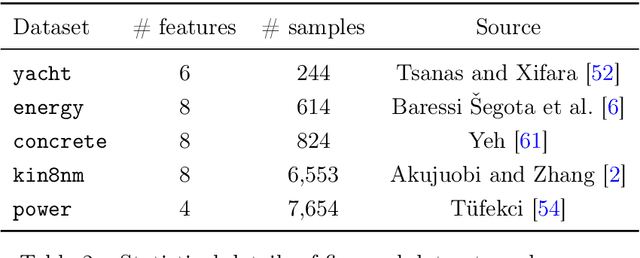
The spectral risk has wide applications in machine learning, especially in real-world decision-making, where people are not only concerned with models' average performance. By assigning different weights to the losses of different sample points, rather than the same weights as in the empirical risk, it allows the model's performance to lie between the average performance and the worst-case performance. In this paper, we propose SOREL, the first stochastic gradient-based algorithm with convergence guarantees for the spectral risk minimization. Previous algorithms often consider adding a strongly concave function to smooth the spectral risk, thus lacking convergence guarantees for the original spectral risk. We theoretically prove that our algorithm achieves a near-optimal rate of $\widetilde{O}(1/\sqrt{\epsilon})$ in terms of $\epsilon$. Experiments on real datasets show that our algorithm outperforms existing algorithms in most cases, both in terms of runtime and sample complexity.