Yuval Filmus
Bandit-Feedback Online Multiclass Classification: Variants and Tradeoffs
Feb 12, 2024Abstract:Consider the domain of multiclass classification within the adversarial online setting. What is the price of relying on bandit feedback as opposed to full information? To what extent can an adaptive adversary amplify the loss compared to an oblivious one? To what extent can a randomized learner reduce the loss compared to a deterministic one? We study these questions in the mistake bound model and provide nearly tight answers. We demonstrate that the optimal mistake bound under bandit feedback is at most $O(k)$ times higher than the optimal mistake bound in the full information case, where $k$ represents the number of labels. This bound is tight and provides an answer to an open question previously posed and studied by Daniely and Helbertal ['13] and by Long ['17, '20], who focused on deterministic learners. Moreover, we present nearly optimal bounds of $\tilde{\Theta}(k)$ on the gap between randomized and deterministic learners, as well as between adaptive and oblivious adversaries in the bandit feedback setting. This stands in contrast to the full information scenario, where adaptive and oblivious adversaries are equivalent, and the gap in mistake bounds between randomized and deterministic learners is a constant multiplicative factor of $2$. In addition, our results imply that in some cases the optimal randomized mistake bound is approximately the square-root of its deterministic parallel. Previous results show that this is essentially the smallest it can get.
Optimal Prediction Using Expert Advice and Randomized Littlestone Dimension
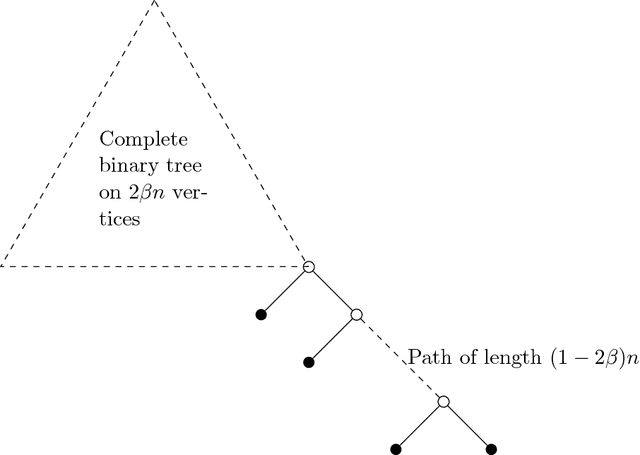
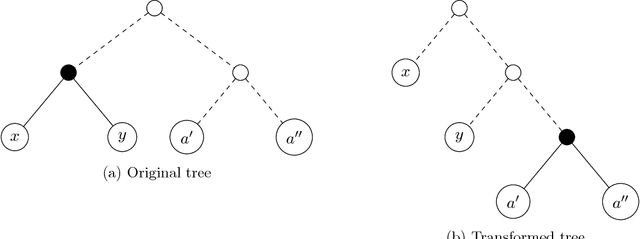
Feb 27, 2023Abstract:A classical result in online learning characterizes the optimal mistake bound achievable by deterministic learners using the Littlestone dimension (Littlestone '88). We prove an analogous result for randomized learners: we show that the optimal expected mistake bound in learning a class $\mathcal{H}$ equals its randomized Littlestone dimension, which is the largest $d$ for which there exists a tree shattered by $\mathcal{H}$ whose average depth is $2d$. We further study optimal mistake bounds in the agnostic case, as a function of the number of mistakes made by the best function in $\mathcal{H}$, denoted by $k$. We show that the optimal randomized mistake bound for learning a class with Littlestone dimension $d$ is $k + \Theta (\sqrt{k d} + d )$. This also implies an optimal deterministic mistake bound of $2k + O (\sqrt{k d} + d )$, thus resolving an open question which was studied by Auer and Long ['99]. As an application of our theory, we revisit the classical problem of prediction using expert advice: about 30 years ago Cesa-Bianchi, Freund, Haussler, Helmbold, Schapire and Warmuth studied prediction using expert advice, provided that the best among the $n$ experts makes at most $k$ mistakes, and asked what are the optimal mistake bounds. Cesa-Bianchi, Freund, Helmbold, and Warmuth ['93, '96] provided a nearly optimal bound for deterministic learners, and left the randomized case as an open problem. We resolve this question by providing an optimal learning rule in the randomized case, and showing that its expected mistake bound equals half of the deterministic bound, up to negligible additive terms. This improves upon previous works by Cesa-Bianchi, Freund, Haussler, Helmbold, Schapire and Warmuth ['93, '97], by Abernethy, Langford, and Warmuth ['06], and by Br\^anzei and Peres ['19], which handled the regimes $k \ll \log n$ or $k \gg \log n$.
A Resilient Distributed Boosting Algorithm
Jun 13, 2022Abstract:Given a learning task where the data is distributed among several parties, communication is one of the fundamental resources which the parties would like to minimize. We present a distributed boosting algorithm which is resilient to a limited amount of noise. Our algorithm is similar to classical boosting algorithms, although it is equipped with a new component, inspired by Impagliazzo's hard-core lemma [Impagliazzo95], adding a robustness quality to the algorithm. We also complement this result by showing that resilience to any asymptotically larger noise is not achievable by a communication-efficient algorithm.
Revisiting the Complexity Analysis of Conflict-Based Search: New Computational Techniques and Improved Bounds
Apr 18, 2021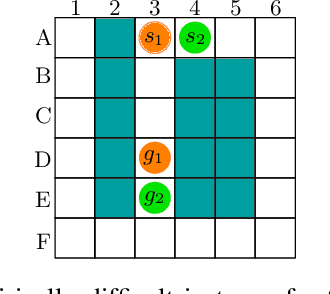
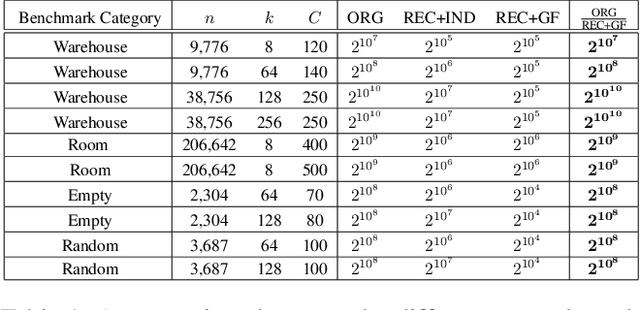
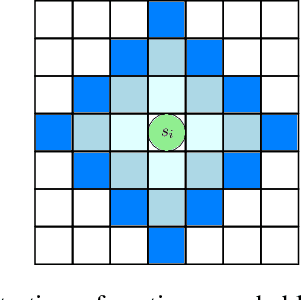
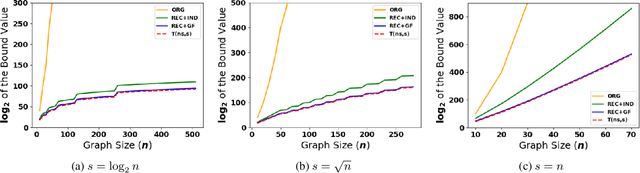
Abstract:The problem of Multi-Agent Path Finding (MAPF) calls for finding a set of conflict-free paths for a fleet of agents operating in a given environment. Arguably, the state-of-the-art approach to computing optimal solutions is Conflict-Based Search (CBS). In this work we revisit the complexity analysis of CBS to provide tighter bounds on the algorithm's run-time in the worst-case. Our analysis paves the way to better pinpoint the parameters that govern (in the worst case) the algorithm's computational complexity. Our analysis is based on two complementary approaches: In the first approach we bound the run-time using the size of a Multi-valued Decision Diagram (MDD) -- a layered graph which compactly contains all possible single-agent paths between two given vertices for a specific path length. In the second approach we express the running time by a novel recurrence relation which bounds the algorithm's complexity. We use generating functions-based analysis in order to tightly bound the recurrence. Using these technique we provide several new upper-bounds on CBS's complexity. The results allow us to improve the existing bound on the running time of CBS for many cases. For example, on a set of common benchmarks we improve the upper-bound by a factor of at least $2^{10^{7}}$.
Twenty (simple) questions
Apr 25, 2017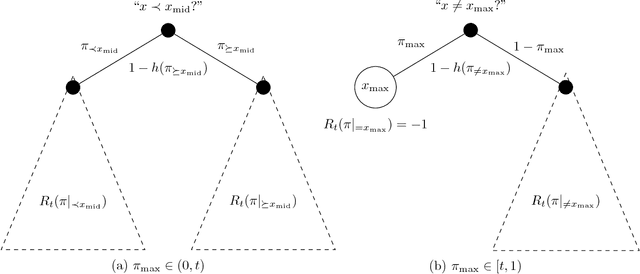
Abstract:A basic combinatorial interpretation of Shannon's entropy function is via the "20 questions" game. This cooperative game is played by two players, Alice and Bob: Alice picks a distribution $\pi$ over the numbers $\{1,\ldots,n\}$, and announces it to Bob. She then chooses a number $x$ according to $\pi$, and Bob attempts to identify $x$ using as few Yes/No queries as possible, on average. An optimal strategy for the "20 questions" game is given by a Huffman code for $\pi$: Bob's questions reveal the codeword for $x$ bit by bit. This strategy finds $x$ using fewer than $H(\pi)+1$ questions on average. However, the questions asked by Bob could be arbitrary. In this paper, we investigate the following question: Are there restricted sets of questions that match the performance of Huffman codes, either exactly or approximately? Our first main result shows that for every distribution $\pi$, Bob has a strategy that uses only questions of the form "$x < c$?" and "$x = c$?", and uncovers $x$ using at most $H(\pi)+1$ questions on average, matching the performance of Huffman codes in this sense. We also give a natural set of $O(rn^{1/r})$ questions that achieve a performance of at most $H(\pi)+r$, and show that $\Omega(rn^{1/r})$ questions are required to achieve such a guarantee. Our second main result gives a set $\mathcal{Q}$ of $1.25^{n+o(n)}$ questions such that for every distribution $\pi$, Bob can implement an optimal strategy for $\pi$ using only questions from $\mathcal{Q}$. We also show that $1.25^{n-o(n)}$ questions are needed, for infinitely many $n$. If we allow a small slack of $r$ over the optimal strategy, then roughly $(rn)^{\Theta(1/r)}$ questions are necessary and sufficient.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge