Learning from weakly dependent data under Dobrushin's condition

Statistical learning theory has largely focused on learning and generalization given independent and identically distributed (i.i.d.) samples. Motivated by applications involving time-series data, there has been a growing literature on learning and generalization in settings where data is sampled from an ergodic process. This work has also developed complexity measures, which appropriately extend the notion of Rademacher complexity to bound the generalization error and learning rates of hypothesis classes in this setting. Rather than time-series data, our work is motivated by settings where data is sampled on a network or a spatial domain, and thus do not fit well within the framework of prior work. We provide learning and generalization bounds for data that are complexly dependent, yet their distribution satisfies the standard Dobrushin's condition. Indeed, we show that the standard complexity measures of Gaussian and Rademacher complexities and VC dimension are sufficient measures of complexity for the purposes of bounding the generalization error and learning rates of hypothesis classes in our setting. Moreover, our generalization bounds only degrade by constant factors compared to their i.i.d. analogs, and our learnability bounds degrade by log factors in the size of the training set.

The Log-Concave Maximum Likelihood Estimator is Optimal in High Dimensions

We study the problem of learning a $d$-dimensional log-concave distribution from $n$ i.i.d. samples with respect to both the squared Hellinger and the total variation distances. We show that for all $d \ge 4$ the maximum likelihood estimator achieves an optimal risk (up to a logarithmic factor) of $O_d(n^{-2/(d+1)}\log(n))$ in terms of squared Hellinger distance. Previously, the optimality of the MLE was known only for $d\le 3$. Additionally, we show that the metric plays a key role, by proving that the minimax risk is at least $\Omega_d(n^{-2/(d+4)})$ in terms of the total variation. Finally, we significantly improve the dimensional constant in the best known lower bound on the risk with respect to the squared Hellinger distance, improving the bound from $2^{-d}n^{-2/(d+1)}$ to $\Omega(n^{-2/(d+1)})$. This implies that estimating a log-concave density up to a fixed accuracy requires a number of samples which is exponential in the dimension.

Space lower bounds for linear prediction

We show that fundamental learning tasks, such as finding an approximate linear separator or linear regression, require memory at least \emph{quadratic} in the dimension, in a natural streaming setting. This implies that such problems cannot be solved (at least in this setting) by scalable memory-efficient streaming algorithms. Our results build on a memory lower bound for a simple linear-algebraic problem -- finding orthogonal vectors -- and utilize the estimates on the packing of the Grassmannian, the manifold of all linear subspaces of fixed dimension.

Detecting Correlations with Little Memory and Communication

We study the problem of identifying correlations in multivariate data, under information constraints: Either on the amount of memory that can be used by the algorithm, or the amount of communication when the data is distributed across several machines. We prove a tight trade-off between the memory/communication complexity and the sample complexity, implying (for example) that to detect pairwise correlations with optimal sample complexity, the number of required memory/communication bits is at least quadratic in the dimension. Our results substantially improve those of Shamir [2014], which studied a similar question in a much more restricted setting. To the best of our knowledge, these are the first provable sample/memory/communication trade-offs for a practical estimation problem, using standard distributions, and in the natural regime where the memory/communication budget is larger than the size of a single data point. To derive our theorems, we prove a new information-theoretic result, which may be relevant for studying other information-constrained learning problems.

A Better Resource Allocation Algorithm with Semi-Bandit Feedback

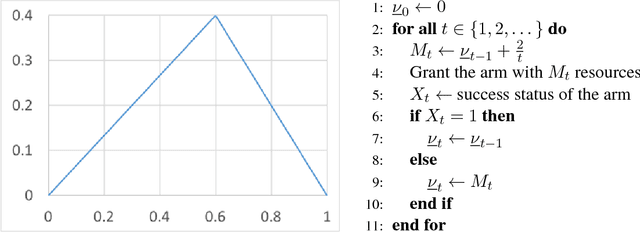
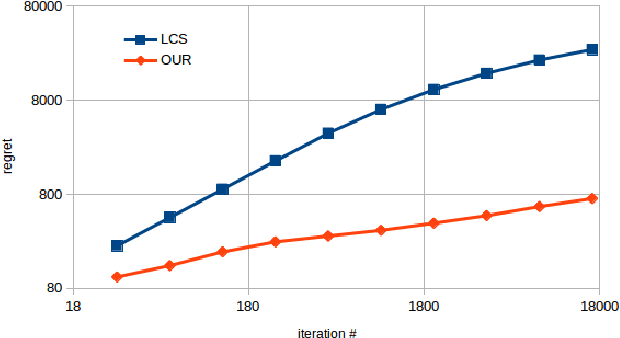
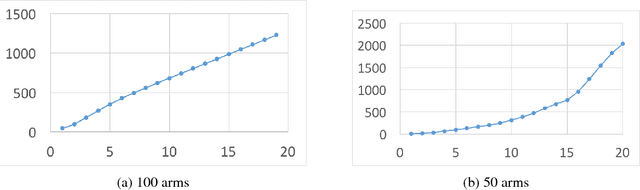
We study a sequential resource allocation problem between a fixed number of arms. On each iteration the algorithm distributes a resource among the arms in order to maximize the expected success rate. Allocating more of the resource to a given arm increases the probability that it succeeds, yet with a cut-off. We follow Lattimore et al. (2014) and assume that the probability increases linearly until it equals one, after which allocating more of the resource is wasteful. These cut-off values are fixed and unknown to the learner. We present an algorithm for this problem and prove a regret upper bound of $O(\log n)$ improving over the best known bound of $O(\log^2 n)$. Lower bounds we prove show that our upper bound is tight. Simulations demonstrate the superiority of our algorithm.

Twenty (simple) questions

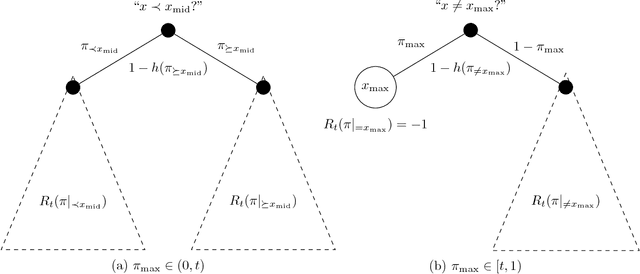
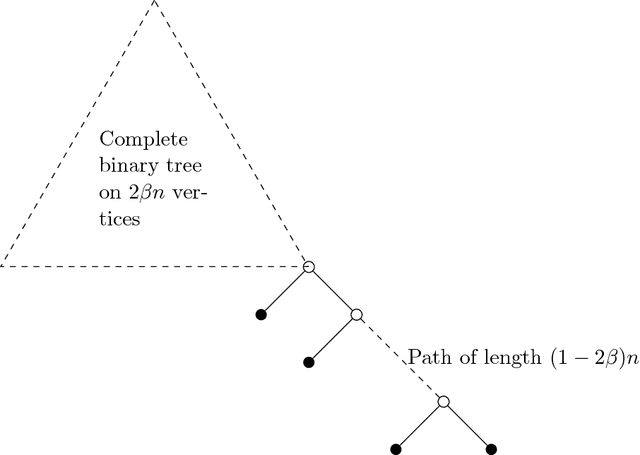
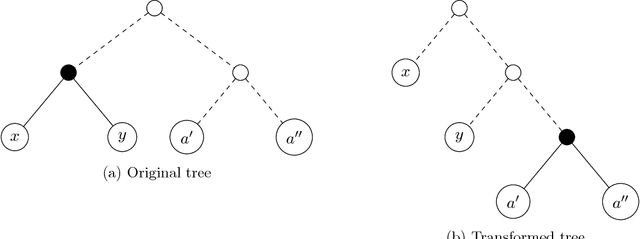
A basic combinatorial interpretation of Shannon's entropy function is via the "20 questions" game. This cooperative game is played by two players, Alice and Bob: Alice picks a distribution $\pi$ over the numbers $\{1,\ldots,n\}$, and announces it to Bob. She then chooses a number $x$ according to $\pi$, and Bob attempts to identify $x$ using as few Yes/No queries as possible, on average. An optimal strategy for the "20 questions" game is given by a Huffman code for $\pi$: Bob's questions reveal the codeword for $x$ bit by bit. This strategy finds $x$ using fewer than $H(\pi)+1$ questions on average. However, the questions asked by Bob could be arbitrary. In this paper, we investigate the following question: Are there restricted sets of questions that match the performance of Huffman codes, either exactly or approximately? Our first main result shows that for every distribution $\pi$, Bob has a strategy that uses only questions of the form "$x < c$?" and "$x = c$?", and uncovers $x$ using at most $H(\pi)+1$ questions on average, matching the performance of Huffman codes in this sense. We also give a natural set of $O(rn^{1/r})$ questions that achieve a performance of at most $H(\pi)+r$, and show that $\Omega(rn^{1/r})$ questions are required to achieve such a guarantee. Our second main result gives a set $\mathcal{Q}$ of $1.25^{n+o(n)}$ questions such that for every distribution $\pi$, Bob can implement an optimal strategy for $\pi$ using only questions from $\mathcal{Q}$. We also show that $1.25^{n-o(n)}$ questions are needed, for infinitely many $n$. If we allow a small slack of $r$ over the optimal strategy, then roughly $(rn)^{\Theta(1/r)}$ questions are necessary and sufficient.