Position: The AI Conference Peer Review Crisis Demands Author Feedback and Reviewer Rewards

The peer review process in major artificial intelligence (AI) conferences faces unprecedented challenges with the surge of paper submissions (exceeding 10,000 submissions per venue), accompanied by growing concerns over review quality and reviewer responsibility. This position paper argues for the need to transform the traditional one-way review system into a bi-directional feedback loop where authors evaluate review quality and reviewers earn formal accreditation, creating an accountability framework that promotes a sustainable, high-quality peer review system. The current review system can be viewed as an interaction between three parties: the authors, reviewers, and system (i.e., conference), where we posit that all three parties share responsibility for the current problems. However, issues with authors can only be addressed through policy enforcement and detection tools, and ethical concerns can only be corrected through self-reflection. As such, this paper focuses on reforming reviewer accountability with systematic rewards through two key mechanisms: (1) a two-stage bi-directional review system that allows authors to evaluate reviews while minimizing retaliatory behavior, (2)a systematic reviewer reward system that incentivizes quality reviewing. We ask for the community's strong interest in these problems and the reforms that are needed to enhance the peer review process.

Computability of Optimizers

Optimization problems are a staple of today's scientific and technical landscape. However, at present, solvers of such problems are almost exclusively run on digital hardware. Using Turing machines as a mathematical model for any type of digital hardware, in this paper, we analyze fundamental limitations of this conceptual approach of solving optimization problems. Since in most applications, the optimizer itself is of significantly more interest than the optimal value of the corresponding function, we will focus on computability of the optimizer. In fact, we will show that in various situations the optimizer is unattainable on Turing machines and consequently on digital computers. Moreover, even worse, there does not exist a Turing machine, which approximates the optimizer itself up to a certain constant error. We prove such results for a variety of well-known problems from very different areas, including artificial intelligence, financial mathematics, and information theory, often deriving the even stronger result that such problems are not Banach-Mazur computable, also not even in an approximate sense.

Stability and Generalization Capabilities of Message Passing Graph Neural Networks

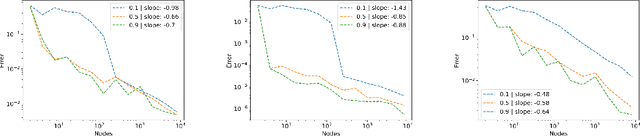
Message passing neural networks (MPNN) have seen a steep rise in popularity since their introduction as generalizations of convolutional neural networks to graph structured data, and are now considered state-of-the-art tools for solving a large variety of graph-focused problems. We study the generalization capabilities of MPNNs in graph classification. We assume that graphs of different classes are sampled from different random graph models. Based on this data distribution, we derive a non-asymptotic bound on the generalization gap between the empirical and statistical loss, that decreases to zero as the graphs become larger. This is proven by showing that a MPNN, applied on a graph, approximates the MPNN applied on the geometric model that the graph discretizes.