Higher-order MRFs based image super resolution: why not MAP?

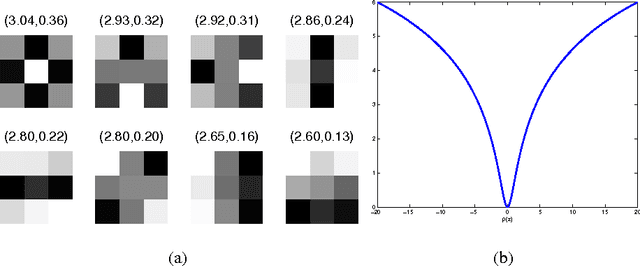
A trainable filter-based higher-order Markov Random Fields (MRFs) model - the so called Fields of Experts (FoE), has proved a highly effective image prior model for many classic image restoration problems. Generally, two options are available to incorporate the learned FoE prior in the inference procedure: (1) sampling-based minimum mean square error (MMSE) estimate, and (2) energy minimization-based maximum a posteriori (MAP) estimate. This letter is devoted to the FoE prior based single image super resolution (SR) problem, and we suggest to make use of the MAP estimate for inference based on two facts: (I) It is well-known that the MAP inference has a remarkable advantage of high computational efficiency, while the sampling-based MMSE estimate is very time consuming. (II) Practical SR experiment results demonstrate that the MAP estimate works equally well compared to the MMSE estimate with exactly the same FoE prior model. Moreover, it can lead to even further improvements by incorporating our discriminatively trained FoE prior model. In summary, we hold that for higher-order natural image prior based SR problem, it is better to employ the MAP estimate for inference.

Fast and Accurate Poisson Denoising with Optimized Nonlinear Diffusion

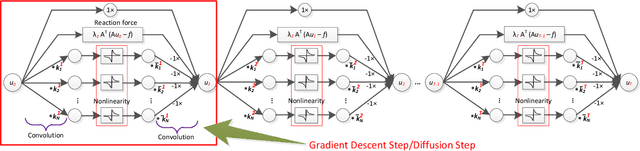
The degradation of the acquired signal by Poisson noise is a common problem for various imaging applications, such as medical imaging, night vision and microscopy. Up to now, many state-of-the-art Poisson denoising techniques mainly concentrate on achieving utmost performance, with little consideration for the computation efficiency. Therefore, in this study we aim to propose an efficient Poisson denoising model with both high computational efficiency and recovery quality. To this end, we exploit the newly-developed trainable nonlinear reaction diffusion model which has proven an extremely fast image restoration approach with performance surpassing recent state-of-the-arts. We retrain the model parameters, including the linear filters and influence functions by taking into account the Poisson noise statistics, and end up with an optimized nonlinear diffusion model specialized for Poisson denoising. The trained model provides strongly competitive results against state-of-the-art approaches, meanwhile bearing the properties of simple structure and high efficiency. Furthermore, our proposed model comes along with an additional advantage, that the diffusion process is well-suited for parallel computation on GPUs. For images of size $512 \times 512$, our GPU implementation takes less than 0.1 seconds to produce state-of-the-art Poisson denoising performance.

On learning optimized reaction diffusion processes for effective image restoration

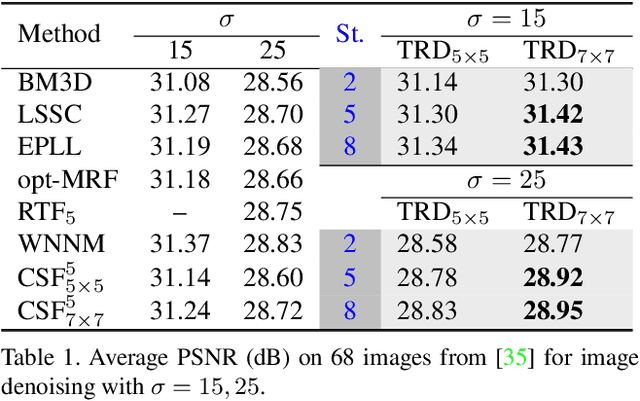
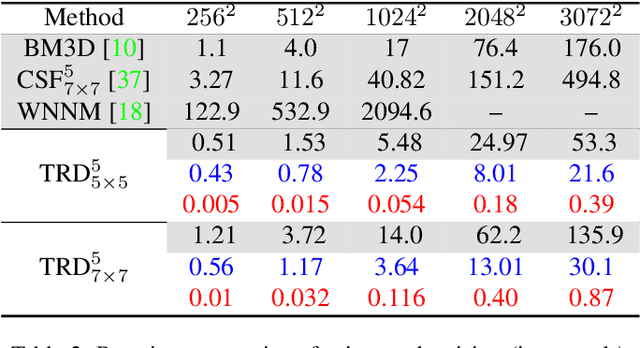
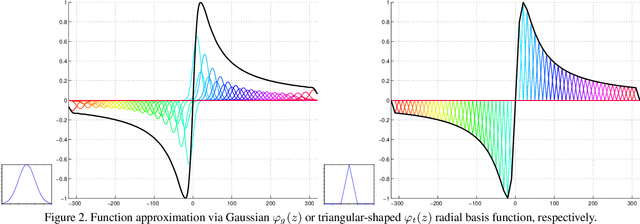
For several decades, image restoration remains an active research topic in low-level computer vision and hence new approaches are constantly emerging. However, many recently proposed algorithms achieve state-of-the-art performance only at the expense of very high computation time, which clearly limits their practical relevance. In this work, we propose a simple but effective approach with both high computational efficiency and high restoration quality. We extend conventional nonlinear reaction diffusion models by several parametrized linear filters as well as several parametrized influence functions. We propose to train the parameters of the filters and the influence functions through a loss based approach. Experiments show that our trained nonlinear reaction diffusion models largely benefit from the training of the parameters and finally lead to the best reported performance on common test datasets for image restoration. Due to their structural simplicity, our trained models are highly efficient and are also well-suited for parallel computation on GPUs.

A higher-order MRF based variational model for multiplicative noise reduction

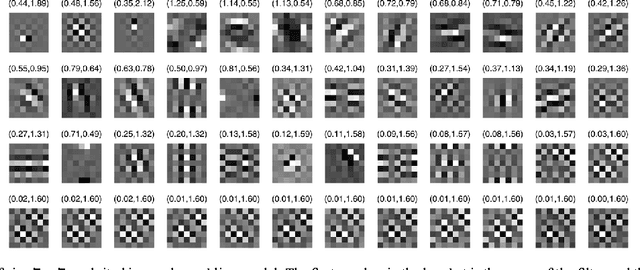
The Fields of Experts (FoE) image prior model, a filter-based higher-order Markov Random Fields (MRF) model, has been shown to be effective for many image restoration problems. Motivated by the successes of FoE-based approaches, in this letter, we propose a novel variational model for multiplicative noise reduction based on the FoE image prior model. The resulted model corresponds to a non-convex minimization problem, which can be solved by a recently published non-convex optimization algorithm. Experimental results based on synthetic speckle noise and real synthetic aperture radar (SAR) images suggest that the performance of our proposed method is on par with the best published despeckling algorithm. Besides, our proposed model comes along with an additional advantage, that the inference is extremely efficient. {Our GPU based implementation takes less than 1s to produce state-of-the-art despeckling performance.}

A bi-level view of inpainting - based image compression

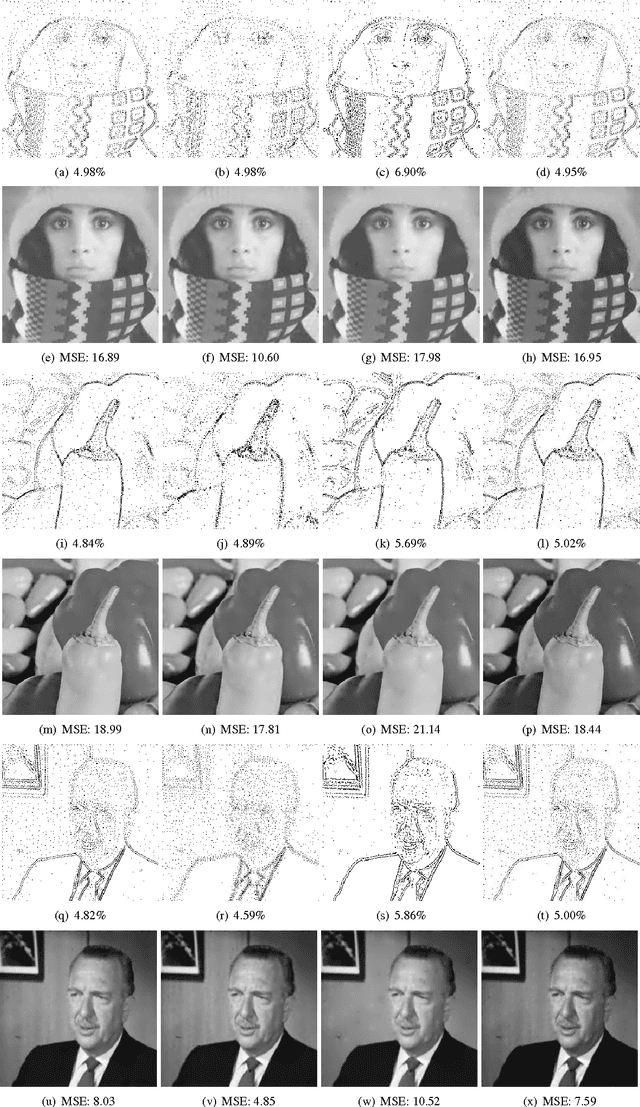
Inpainting based image compression approaches, especially linear and non-linear diffusion models, are an active research topic for lossy image compression. The major challenge in these compression models is to find a small set of descriptive supporting points, which allow for an accurate reconstruction of the original image. It turns out in practice that this is a challenging problem even for the simplest Laplacian interpolation model. In this paper, we revisit the Laplacian interpolation compression model and introduce two fast algorithms, namely successive preconditioning primal dual algorithm and the recently proposed iPiano algorithm, to solve this problem efficiently. Furthermore, we extend the Laplacian interpolation based compression model to a more general form, which is based on principles from bi-level optimization. We investigate two different variants of the Laplacian model, namely biharmonic interpolation and smoothed Total Variation regularization. Our numerical results show that significant improvements can be obtained from the biharmonic interpolation model, and it can recover an image with very high quality from only 5% pixels.

iPiano: Inertial Proximal Algorithm for Non-Convex Optimization

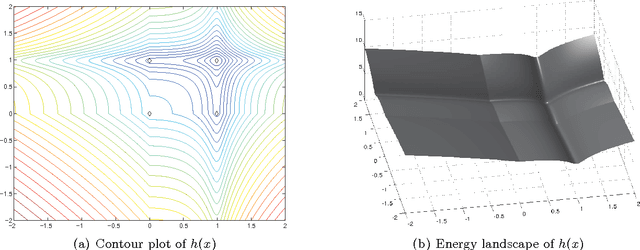
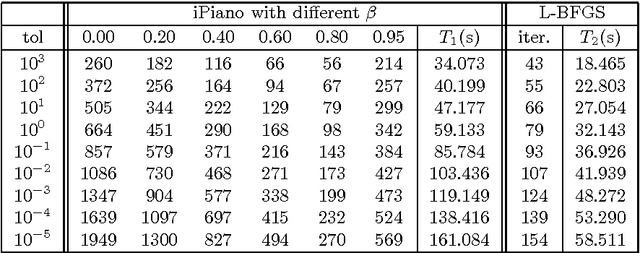
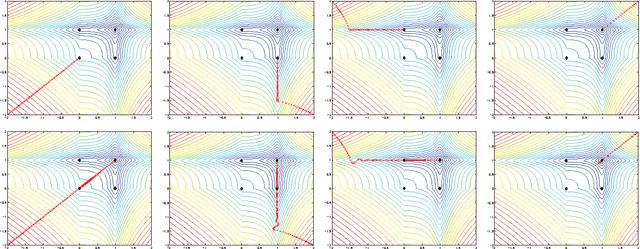
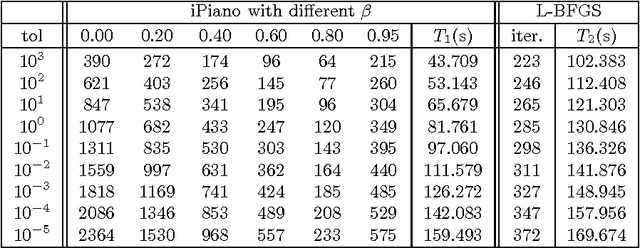
In this paper we study an algorithm for solving a minimization problem composed of a differentiable (possibly non-convex) and a convex (possibly non-differentiable) function. The algorithm iPiano combines forward-backward splitting with an inertial force. It can be seen as a non-smooth split version of the Heavy-ball method from Polyak. A rigorous analysis of the algorithm for the proposed class of problems yields global convergence of the function values and the arguments. This makes the algorithm robust for usage on non-convex problems. The convergence result is obtained based on the \KL inequality. This is a very weak restriction, which was used to prove convergence for several other gradient methods. First, an abstract convergence theorem for a generic algorithm is proved, and, then iPiano is shown to satisfy the requirements of this theorem. Furthermore, a convergence rate is established for the general problem class. We demonstrate iPiano on computer vision problems: image denoising with learned priors and diffusion based image compression.

Revisiting loss-specific training of filter-based MRFs for image restoration

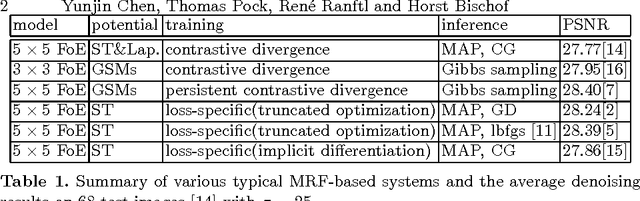
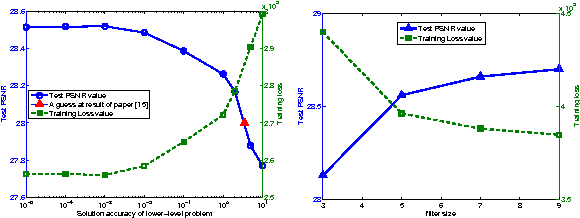
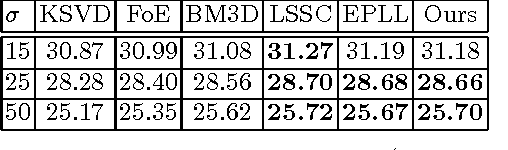
It is now well known that Markov random fields (MRFs) are particularly effective for modeling image priors in low-level vision. Recent years have seen the emergence of two main approaches for learning the parameters in MRFs: (1) probabilistic learning using sampling-based algorithms and (2) loss-specific training based on MAP estimate. After investigating existing training approaches, it turns out that the performance of the loss-specific training has been significantly underestimated in existing work. In this paper, we revisit this approach and use techniques from bi-level optimization to solve it. We show that we can get a substantial gain in the final performance by solving the lower-level problem in the bi-level framework with high accuracy using our newly proposed algorithm. As a result, our trained model is on par with highly specialized image denoising algorithms and clearly outperforms probabilistically trained MRF models. Our findings suggest that for the loss-specific training scheme, solving the lower-level problem with higher accuracy is beneficial. Our trained model comes along with the additional advantage, that inference is extremely efficient. Our GPU-based implementation takes less than 1s to produce state-of-the-art performance.

Learning $\ell_1$-based analysis and synthesis sparsity priors using bi-level optimization

We consider the analysis operator and synthesis dictionary learning problems based on the the $\ell_1$ regularized sparse representation model. We reveal the internal relations between the $\ell_1$-based analysis model and synthesis model. We then introduce an approach to learn both analysis operator and synthesis dictionary simultaneously by using a unified framework of bi-level optimization. Our aim is to learn a meaningful operator (dictionary) such that the minimum energy solution of the analysis (synthesis)-prior based model is as close as possible to the ground-truth. We solve the bi-level optimization problem using the implicit differentiation technique. Moreover, we demonstrate the effectiveness of our leaning approach by applying the learned analysis operator (dictionary) to the image denoising task and comparing its performance with state-of-the-art methods. Under this unified framework, we can compare the performance of the two types of priors.

Insights into analysis operator learning: From patch-based sparse models to higher-order MRFs

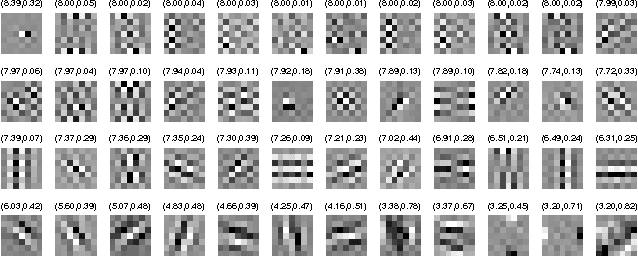
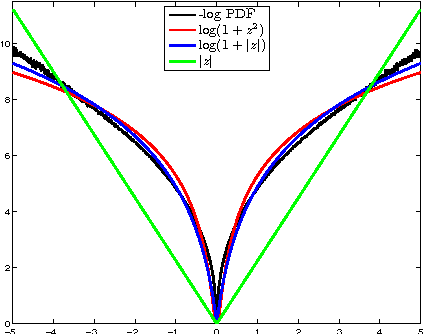
This paper addresses a new learning algorithm for the recently introduced co-sparse analysis model. First, we give new insights into the co-sparse analysis model by establishing connections to filter-based MRF models, such as the Field of Experts (FoE) model of Roth and Black. For training, we introduce a technique called bi-level optimization to learn the analysis operators. Compared to existing analysis operator learning approaches, our training procedure has the advantage that it is unconstrained with respect to the analysis operator. We investigate the effect of different aspects of the co-sparse analysis model and show that the sparsity promoting function (also called penalty function) is the most important factor in the model. In order to demonstrate the effectiveness of our training approach, we apply our trained models to various classical image restoration problems. Numerical experiments show that our trained models clearly outperform existing analysis operator learning approaches and are on par with state-of-the-art image denoising algorithms. Our approach develops a framework that is intuitive to understand and easy to implement.