Partial Gradient Optimal Thresholding Algorithms for a Class of Sparse Optimization Problems

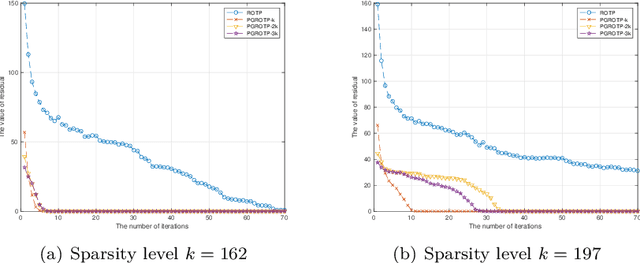
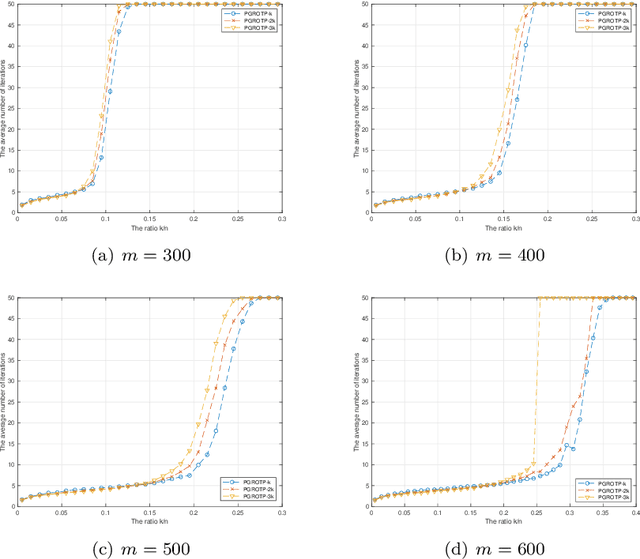
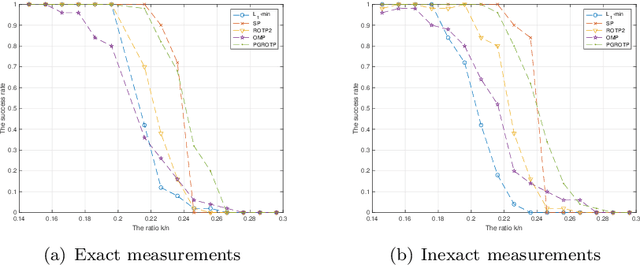
The optimization problems with a sparsity constraint is a class of important global optimization problems. A typical type of thresholding algorithms for solving such a problem adopts the traditional full steepest descent direction or Newton-like direction as a search direction to generate an iterate on which a certain thresholding is performed. Traditional hard thresholding discards a large part of a vector when the vector is dense. Thus a large part of important information contained in a dense vector has been lost in such a thresholding process. Recent study [Zhao, SIAM J Optim, 30(1), pp. 31-55, 2020] shows that the hard thresholding should be applied to a compressible vector instead of a dense vector to avoid a big loss of information. On the other hand, the optimal $k$-thresholding as a novel thresholding technique may overcome the intrinsic drawback of hard thresholding, and performs thresholding and objective function minimization simultaneously. This motivates us to propose the so-called partial gradient optimal thresholding method in this paper, which is an integration of the partial gradient and the optimal $k$-thresholding technique. The solution error bound and convergence for the proposed algorithms have been established in this paper under suitable conditions. Application of our results to the sparse optimization problems arising from signal recovery is also discussed. Experiment results from synthetic data indicate that the proposed algorithm called PGROTP is efficient and comparable to several existing algorithms.

Newton-Type Optimal Thresholding Algorithms for Sparse Optimization Problems

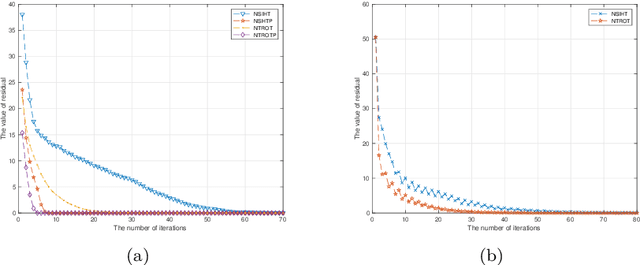
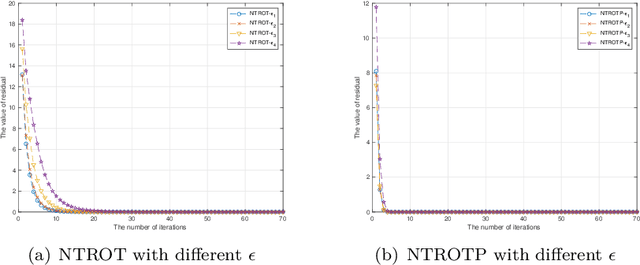
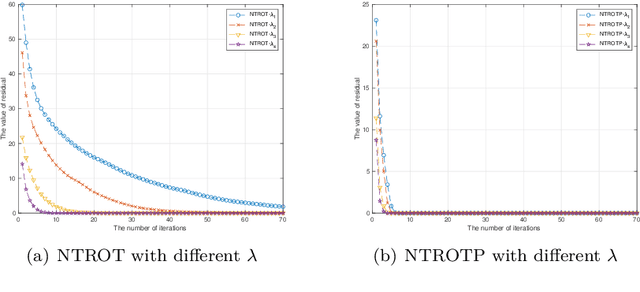
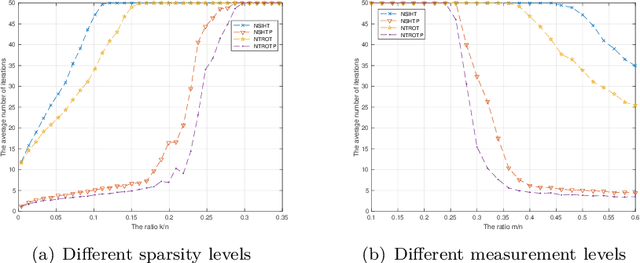
Sparse signals can be possibly reconstructed by an algorithm which merges a traditional nonlinear optimization method and a certain thresholding technique. Different from existing thresholding methods, a novel thresholding technique referred to as the optimal $k$-thresholding was recently proposed by Zhao [SIAM J Optim, 30(1), pp. 31-55, 2020]. This technique simultaneously performs the minimization of an error metric for the problem and thresholding of the iterates generated by the classic gradient method. In this paper, we propose the so-called Newton-type optimal $k$-thresholding (NTOT) algorithm which is motivated by the appreciable performance of both Newton-type methods and the optimal $k$-thresholding technique for signal recovery. The guaranteed performance (including convergence) of the proposed algorithms are shown in terms of suitable choices of the algorithmic parameters and the restricted isometry property (RIP) of the sensing matrix which has been widely used in the analysis of compressive sensing algorithms. The simulation results based on synthetic signals indicate that the proposed algorithms are stable and efficient for signal recovery.