Learning Beyond Experience: Generalizing to Unseen State Space with Reservoir Computing

Machine learning techniques offer an effective approach to modeling dynamical systems solely from observed data. However, without explicit structural priors -- built-in assumptions about the underlying dynamics -- these techniques typically struggle to generalize to aspects of the dynamics that are poorly represented in the training data. Here, we demonstrate that reservoir computing -- a simple, efficient, and versatile machine learning framework often used for data-driven modeling of dynamical systems -- can generalize to unexplored regions of state space without explicit structural priors. First, we describe a multiple-trajectory training scheme for reservoir computers that supports training across a collection of disjoint time series, enabling effective use of available training data. Then, applying this training scheme to multistable dynamical systems, we show that RCs trained on trajectories from a single basin of attraction can achieve out-of-domain generalization by capturing system behavior in entirely unobserved basins.

Context parroting: A simple but tough-to-beat baseline for foundation models in scientific machine learning

Recently-developed time series foundation models for scientific machine learning exhibit emergent abilities to predict physical systems. These abilities include zero-shot forecasting, in which a model forecasts future states of a system given only a short trajectory as context. Here, we show that foundation models applied to physical systems can give accurate predictions, but that they fail to develop meaningful representations of the underlying physics. Instead, foundation models often forecast by context parroting, a simple zero-shot forecasting strategy that copies directly from the context. As a result, a naive direct context parroting model scores higher than state-of-the-art time-series foundation models on predicting a diverse range of dynamical systems, at a tiny fraction of the computational cost. We draw a parallel between context parroting and induction heads, which explains why large language models trained on text can be repurposed for time series forecasting. Our dynamical systems perspective also ties the scaling between forecast accuracy and context length to the fractal dimension of the attractor, providing insight into the previously observed in-context neural scaling laws. Context parroting thus serves as a simple but tough-to-beat baseline for future time-series foundation models and can help identify in-context learning strategies beyond parroting.

Zero-shot forecasting of chaotic systems

Time-series forecasting is a challenging task that traditionally requires specialized models custom-trained for the specific task at hand. Recently, inspired by the success of large language models, foundation models pre-trained on vast amounts of time-series data from diverse domains have emerged as a promising candidate for general-purpose time-series forecasting. The defining characteristic of these foundation models is their ability to perform zero-shot learning, that is, forecasting a new system from limited context data without explicit re-training or fine-tuning. Here, we evaluate whether the zero-shot learning paradigm extends to the challenging task of forecasting chaotic systems. Across 135 distinct chaotic dynamical systems and $10^8$ timepoints, we find that foundation models produce competitive forecasts compared to custom-trained models (including NBEATS, TiDE, etc.), particularly when training data is limited. Interestingly, even after point forecasts fail, foundation models preserve the geometric and statistical properties of the chaotic attractors, demonstrating a surprisingly strong ability to capture the long-term behavior of chaotic dynamical systems. Our results highlight the promises and pitfalls of foundation models in making zero-shot forecasts of chaotic systems.

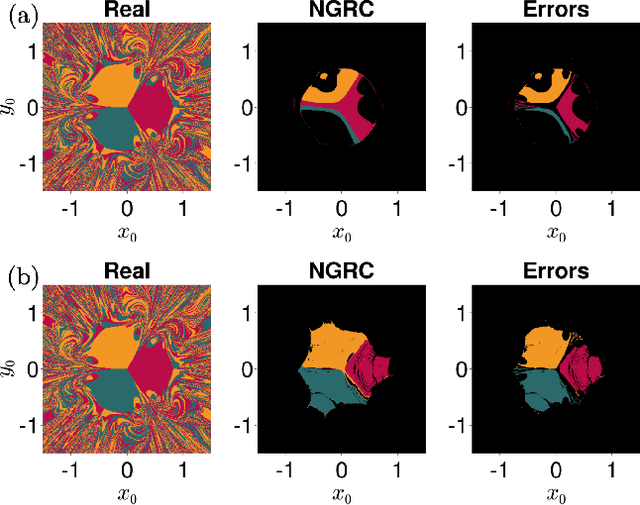
How more data can hurt: Instability and regularization in next-generation reservoir computing

It has been found recently that more data can, counter-intuitively, hurt the performance of deep neural networks. Here, we show that a more extreme version of the phenomenon occurs in data-driven models of dynamical systems. To elucidate the underlying mechanism, we focus on next-generation reservoir computing (NGRC) -- a popular framework for learning dynamics from data. We find that, despite learning a better representation of the flow map with more training data, NGRC can adopt an ill-conditioned ``integrator'' and lose stability. We link this data-induced instability to the auxiliary dimensions created by the delayed states in NGRC. Based on these findings, we propose simple strategies to mitigate the instability, either by increasing regularization strength in tandem with data size, or by carefully introducing noise during training. Our results highlight the importance of proper regularization in data-driven modeling of dynamical systems.

A Catch-22 of Reservoir Computing

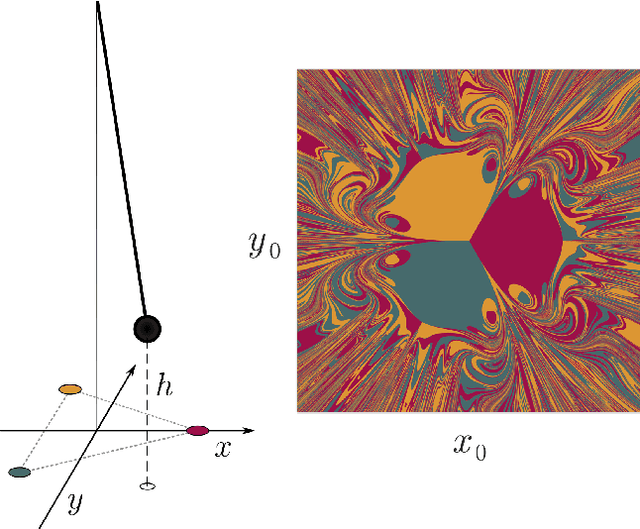
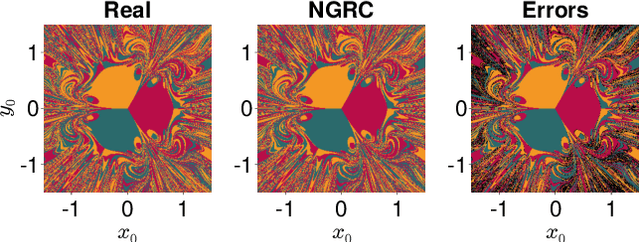
Reservoir Computing (RC) is a simple and efficient model-free framework for data-driven predictions of nonlinear dynamical systems. Recently, Next Generation Reservoir Computing (NGRC) has emerged as an especially attractive variant of RC. By shifting the nonlinearity from the reservoir to the readout layer, NGRC requires less data and has fewer hyperparameters to optimize, making it suitable for challenging tasks such as predicting basins of attraction. Here, using paradigmatic multistable systems including magnetic pendulums and coupled Kuramoto oscillators, we show that the performance of NGRC models can be extremely sensitive to the choice of readout nonlinearity. In particular, by incorporating the exact nonlinearity from the original equations, NGRC trained on a single trajectory can predict pseudo-fractal basins with almost perfect accuracy. However, even a small uncertainty on the exact nonlinearity can completely break NGRC, rendering the prediction accuracy no better than chance. This creates a catch-22 for NGRC since it may not be able to make useful predictions unless a key part of the system being predicted (i.e., its nonlinearity) is already known. Our results highlight the challenges faced by data-driven methods in learning complex dynamical systems.

Learning medical triage from clinicians using Deep Q-Learning

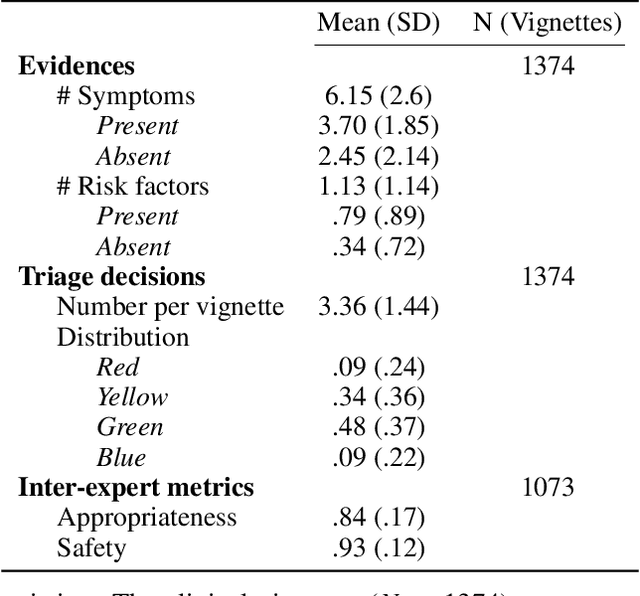
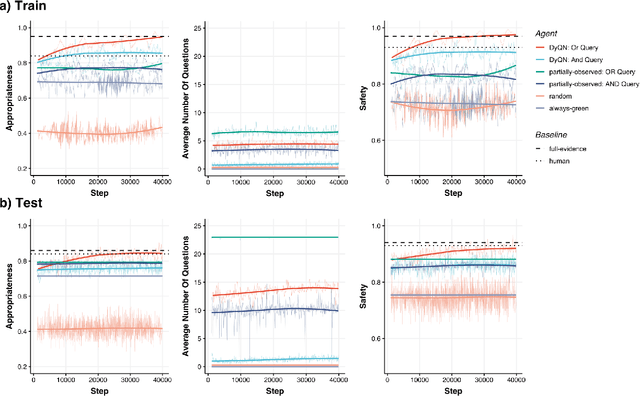
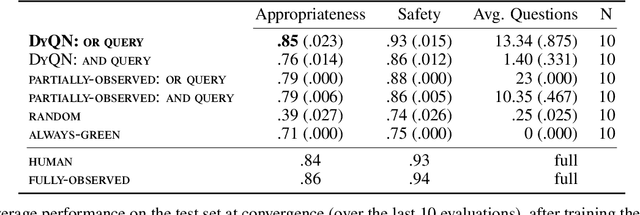
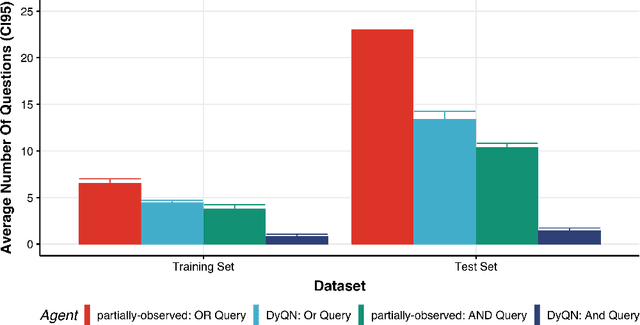
Medical Triage is of paramount importance to healthcare systems, allowing for the correct orientation of patients and allocation of the necessary resources to treat them adequately. While reliable decision-tree methods exist to triage patients based on their presentation, those trees implicitly require human inference and are not immediately applicable in a fully automated setting. On the other hand, learning triage policies directly from experts may correct for some of the limitations of hard-coded decision-trees. In this work, we present a Deep Reinforcement Learning approach (a variant of DeepQ-Learning) to triage patients using curated clinical vignettes. The dataset, consisting of 1374 clinical vignettes, was created by medical doctors to represent real-life cases. Each vignette is associated with an average of 3.8 expert triage decisions given by medical doctors relying solely on medical history. We show that this approach is on a par with human performance, yielding safe triage decisions in 94% of cases, and matching expert decisions in 85% of cases. The trained agent learns when to stop asking questions, acquires optimized decision policies requiring less evidence than supervised approaches, and adapts to the novelty of a situation by asking for more information. Overall, we demonstrate that a Deep Reinforcement Learning approach can learn effective medical triage policies directly from expert decisions, without requiring expert knowledge engineering. This approach is scalable and can be deployed in healthcare settings or geographical regions with distinct triage specifications, or where trained experts are scarce, to improve decision making in the early stage of care.