Beyond Fixed Psychological Personas: State Beats Trait, but Language Models are State-Blind

User interactions with language models vary due to static properties of the user (trait) and the specific context of the interaction (state). However, existing persona datasets (like PersonaChat, PANDORA etc.) capture only trait, and ignore the impact of state. We introduce Chameleon, a dataset of 5,001 contextual psychological profiles from 1,667 Reddit users, each measured across multiple contexts. Using the Chameleon dataset, we present three key findings. First, inspired by Latent State-Trait theory, we decompose variance and find that 74\% is within-person(state) while only 26\% is between-person (trait). Second, we find that LLMs are state-blind: they focus on trait only, and produce similar responses regardless of state. Third, we find that reward models react to user state, but inconsistently: different models favor or penalize the same users in opposite directions. We release Chameleon to support research on affective computing, personalized dialogue, and RLHF alignment.

Uniform-in-Time Weak Error Analysis for Stochastic Gradient Descent Algorithms via Diffusion Approximation

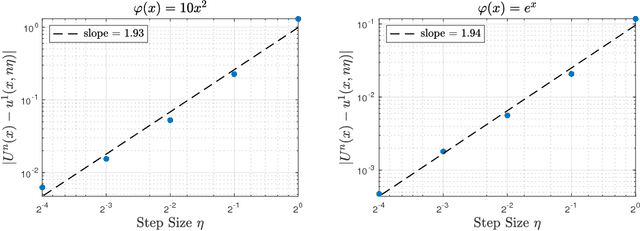
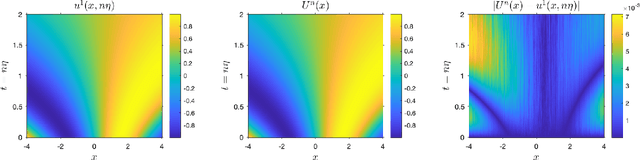
Diffusion approximation provides weak approximation for stochastic gradient descent algorithms in a finite time horizon. In this paper, we introduce new tools motivated by the backward error analysis of numerical stochastic differential equations into the theoretical framework of diffusion approximation, extending the validity of the weak approximation from finite to infinite time horizon. The new techniques developed in this paper enable us to characterize the asymptotic behavior of constant-step-size SGD algorithms for strongly convex objective functions, a goal previously unreachable within the diffusion approximation framework. Our analysis builds upon a truncated formal power expansion of the solution of a stochastic modified equation arising from diffusion approximation, where the main technical ingredient is a uniform-in-time weak error bound controlling the long-term behavior of the expansion coefficient functions near the global minimum. We expect these new techniques to greatly expand the range of applicability of diffusion approximation to cover wider and deeper aspects of stochastic optimization algorithms in data science.