Omics-scale polymer computational database transferable to real-world artificial intelligence applications

Developing large-scale foundational datasets is a critical milestone in advancing artificial intelligence (AI)-driven scientific innovation. However, unlike AI-mature fields such as natural language processing, materials science, particularly polymer research, has significantly lagged in developing extensive open datasets. This lag is primarily due to the high costs of polymer synthesis and property measurements, along with the vastness and complexity of the chemical space. This study presents PolyOmics, an omics-scale computational database generated through fully automated molecular dynamics simulation pipelines that provide diverse physical properties for over $10^5$ polymeric materials. The PolyOmics database is collaboratively developed by approximately 260 researchers from 48 institutions to bridge the gap between academia and industry. Machine learning models pretrained on PolyOmics can be efficiently fine-tuned for a wide range of real-world downstream tasks, even when only limited experimental data are available. Notably, the generalisation capability of these simulation-to-real transfer models improve significantly as the size of the PolyOmics database increases, exhibiting power-law scaling. The emergence of scaling laws supports the "more is better" principle, highlighting the significance of ultralarge-scale computational materials data for improving real-world prediction performance. This unprecedented omics-scale database reveals vast unexplored regions of polymer materials, providing a foundation for AI-driven polymer science.

Scaling Law of Sim2Real Transfer Learning in Expanding Computational Materials Databases for Real-World Predictions

To address the challenge of limited experimental materials data, extensive physical property databases are being developed based on high-throughput computational experiments, such as molecular dynamics simulations. Previous studies have shown that fine-tuning a predictor pretrained on a computational database to a real system can result in models with outstanding generalization capabilities compared to learning from scratch. This study demonstrates the scaling law of simulation-to-real (Sim2Real) transfer learning for several machine learning tasks in materials science. Case studies of three prediction tasks for polymers and inorganic materials reveal that the prediction error on real systems decreases according to a power-law as the size of the computational data increases. Observing the scaling behavior offers various insights for database development, such as determining the sample size necessary to achieve a desired performance, identifying equivalent sample sizes for physical and computational experiments, and guiding the design of data production protocols for downstream real-world tasks.

Transfer learning with affine model transformation

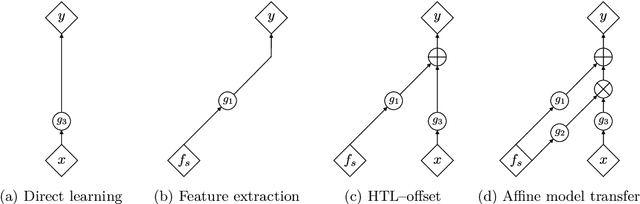
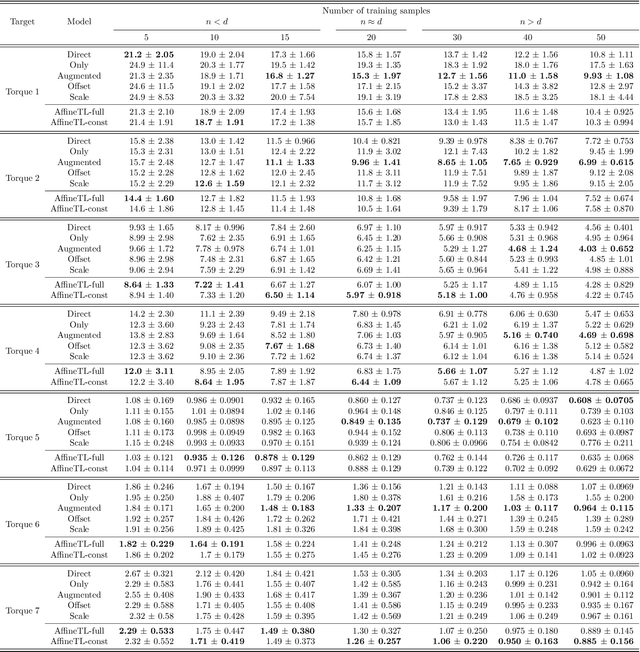
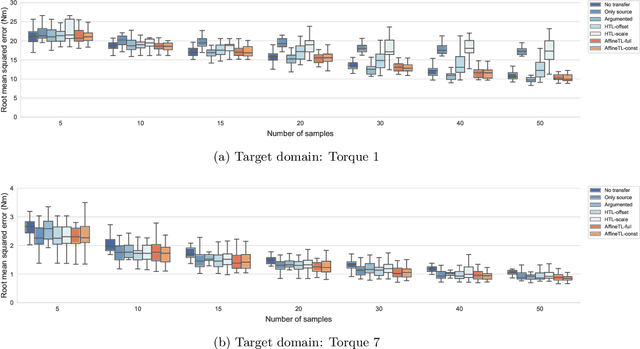
Supervised transfer learning (TL) has received considerable attention because of its potential to boost the predictive power of machine learning in cases with limited data. In a conventional scenario, cross-domain differences are modeled and estimated using a given set of source models and samples from a target domain. For example, if there is a functional relationship between source and target domains, only domain-specific factors are additionally learned using target samples to shift the source models to the target. However, the general methodology for modeling and estimating such cross-domain shifts has been less studied. This study presents a TL framework that simultaneously and separately estimates domain shifts and domain-specific factors using given target samples. Assuming consistency and invertibility of the domain transformation functions, we derive an optimal family of functions to represent the cross-domain shift. The newly derived class of transformation functions takes the same form as invertible neural networks using affine coupling layers, which are widely used in generative deep learning. We show that the proposed method encompasses a wide range of existing methods, including the most common TL procedure based on feature extraction using neural networks. We also clarify the theoretical properties of the proposed method, such as the convergence rate of the generalization error, and demonstrate the practical benefits of separately modeling and estimating domain-specific factors through several case studies.