Synthetic-Powered Predictive Inference

Conformal prediction is a framework for predictive inference with a distribution-free, finite-sample guarantee. However, it tends to provide uninformative prediction sets when calibration data are scarce. This paper introduces Synthetic-powered predictive inference (SPPI), a novel framework that incorporates synthetic data -- e.g., from a generative model -- to improve sample efficiency. At the core of our method is a score transporter: an empirical quantile mapping that aligns nonconformity scores from trusted, real data with those from synthetic data. By carefully integrating the score transporter into the calibration process, SPPI provably achieves finite-sample coverage guarantees without making any assumptions about the real and synthetic data distributions. When the score distributions are well aligned, SPPI yields substantially tighter and more informative prediction sets than standard conformal prediction. Experiments on image classification and tabular regression demonstrate notable improvements in predictive efficiency in data-scarce settings.

Binary classification with corrupted labels

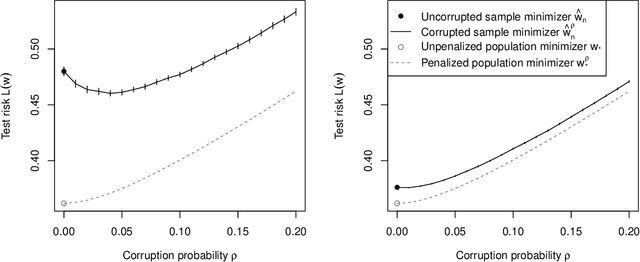
In a binary classification problem where the goal is to fit an accurate predictor, the presence of corrupted labels in the training data set may create an additional challenge. However, in settings where likelihood maximization is poorly behaved-for example, if positive and negative labels are perfectly separable-then a small fraction of corrupted labels can improve performance by ensuring robustness. In this work, we establish that in such settings, corruption acts as a form of regularization, and we compute precise upper bounds on estimation error in the presence of corruptions. Our results suggest that the presence of corrupted data points is beneficial only up to a small fraction of the total sample, scaling with the square root of the sample size.