Capturing the diversity of biological tuning curves using generative adversarial networks

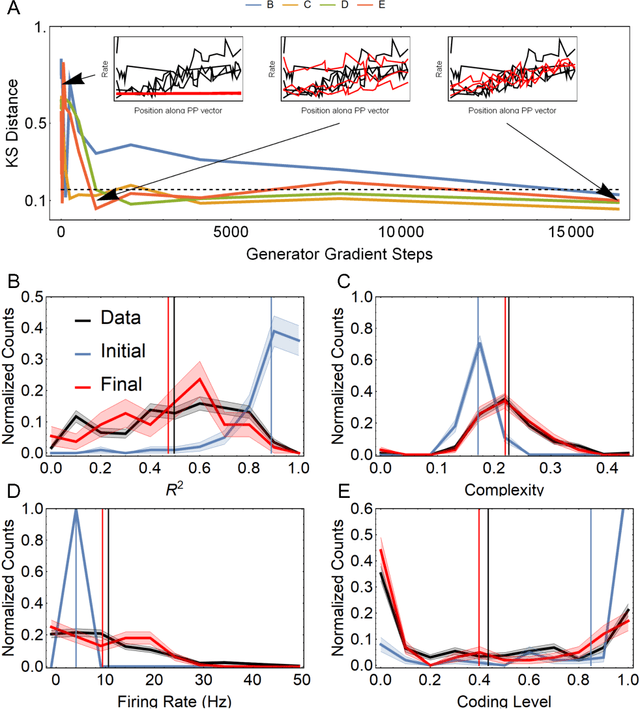
Tuning curves characterizing the response selectivities of biological neurons often exhibit large degrees of irregularity and diversity across neurons. Theoretical network models that feature heterogeneous cell populations or random connectivity also give rise to diverse tuning curves. However, a general framework for fitting such models to experimentally measured tuning curves is lacking. We address this problem by proposing to view mechanistic network models as generative models whose parameters can be optimized to fit the distribution of experimentally measured tuning curves. A major obstacle for fitting such models is that their likelihood function is not explicitly available or is highly intractable to compute. Recent advances in machine learning provide ways for fitting generative models without the need to evaluate the likelihood and its gradient. Generative Adversarial Networks (GAN) provide one such framework which has been successful in traditional machine learning tasks. We apply this approach in two separate experiments, showing how GANs can be used to fit commonly used mechanistic models in theoretical neuroscience to datasets of measured tuning curves. This fitting procedure avoids the computationally expensive step of inferring latent variables, e.g. the biophysical parameters of individual cells or the particular realization of the full synaptic connectivity matrix, and directly learns model parameters which characterize the statistics of connectivity or of single-cell properties. Another strength of this approach is that it fits the entire, joint distribution of experimental tuning curves, instead of matching a few summary statistics picked a priori by the user. More generally, this framework opens the door to fitting theoretically motivated dynamical network models directly to simultaneously or non-simultaneously recorded neural responses.

Learning unbelievable marginal probabilities

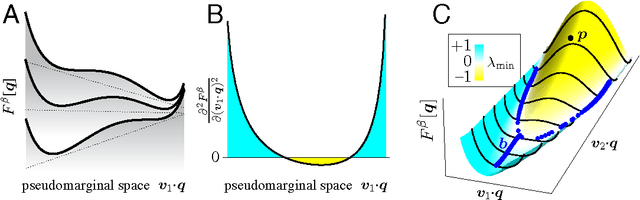
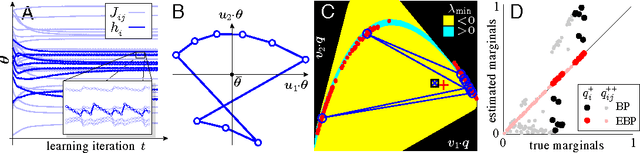
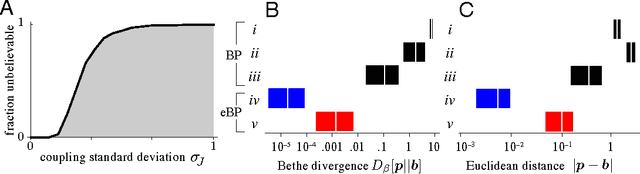
Loopy belief propagation performs approximate inference on graphical models with loops. One might hope to compensate for the approximation by adjusting model parameters. Learning algorithms for this purpose have been explored previously, and the claim has been made that every set of locally consistent marginals can arise from belief propagation run on a graphical model. On the contrary, here we show that many probability distributions have marginals that cannot be reached by belief propagation using any set of model parameters or any learning algorithm. We call such marginals `unbelievable.' This problem occurs whenever the Hessian of the Bethe free energy is not positive-definite at the target marginals. All learning algorithms for belief propagation necessarily fail in these cases, producing beliefs or sets of beliefs that may even be worse than the pre-learning approximation. We then show that averaging inaccurate beliefs, each obtained from belief propagation using model parameters perturbed about some learned mean values, can achieve the unbelievable marginals.