The biglasso Package: A Memory- and Computation-Efficient Solver for Lasso Model Fitting with Big Data in R

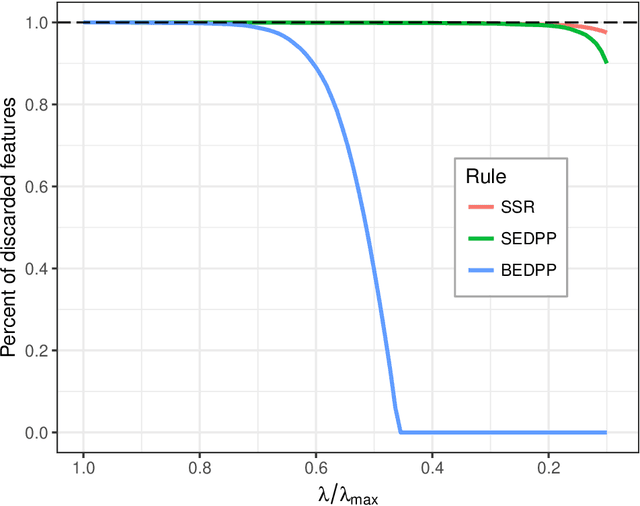
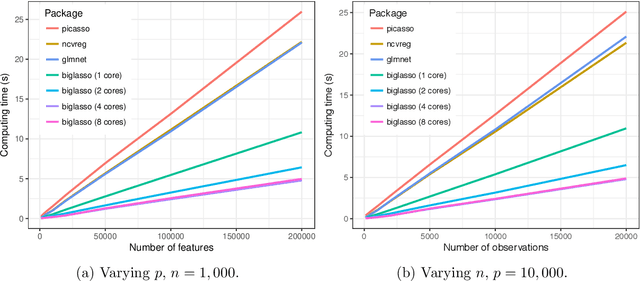
Penalized regression models such as the lasso have been extensively applied to analyzing high-dimensional data sets. However, due to memory limitations, existing R packages like glmnet and ncvreg are not capable of fitting lasso-type models for ultrahigh-dimensional, multi-gigabyte data sets that are increasingly seen in many areas such as genetics, genomics, biomedical imaging, and high-frequency finance. In this research, we implement an R package called biglasso that tackles this challenge. biglasso utilizes memory-mapped files to store the massive data on the disk, only reading data into memory when necessary during model fitting, and is thus able to handle out-of-core computation seamlessly. Moreover, it's equipped with newly proposed, more efficient feature screening rules, which substantially accelerate the computation. Benchmarking experiments show that our biglasso package, as compared to existing popular ones like glmnet, is much more memory- and computation-efficient. We further analyze a 31 GB real data set on a laptop with only 16 GB RAM to demonstrate the out-of-core computation capability of biglasso in analyzing massive data sets that cannot be accommodated by existing R packages.

Efficient Feature Screening for Lasso-Type Problems via Hybrid Safe-Strong Rules

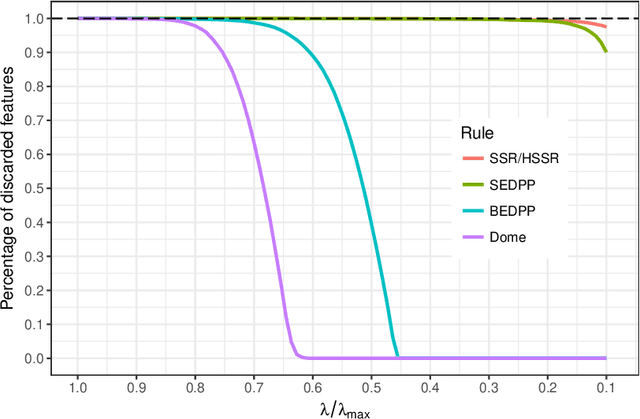
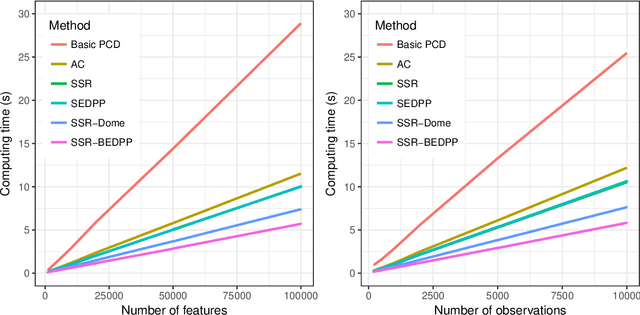
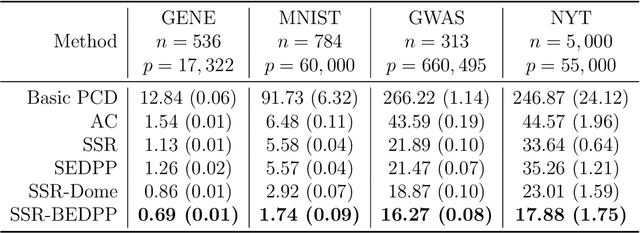
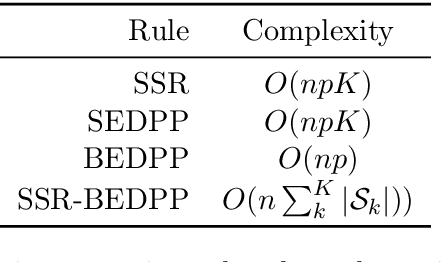
The lasso model has been widely used for model selection in data mining, machine learning, and high-dimensional statistical analysis. However, due to the ultrahigh-dimensional, large-scale data sets collected in many real-world applications, it remains challenging to solve the lasso problems even with state-of-the-art algorithms. Feature screening is a powerful technique for addressing the Big Data challenge by discarding inactive features from the lasso optimization. In this paper, we propose a family of hybrid safe-strong rules (HSSR) which incorporate safe screening rules into the sequential strong rule (SSR) to remove unnecessary computational burden. In particular, we present two instances of HSSR, namely SSR-Dome and SSR-BEDPP, for the standard lasso problem. We further extend SSR-BEDPP to the elastic net and group lasso problems to demonstrate the generalizability of the hybrid screening idea. Extensive numerical experiments with synthetic and real data sets are conducted for both the standard lasso and the group lasso problems. Results show that our proposed hybrid rules substantially outperform existing state-of-the-art rules.