Finding GEMS: Multi-Scale Dictionaries for High-Dimensional Graph Signals

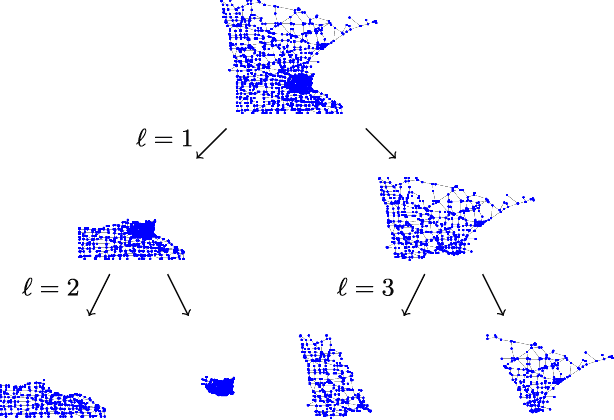
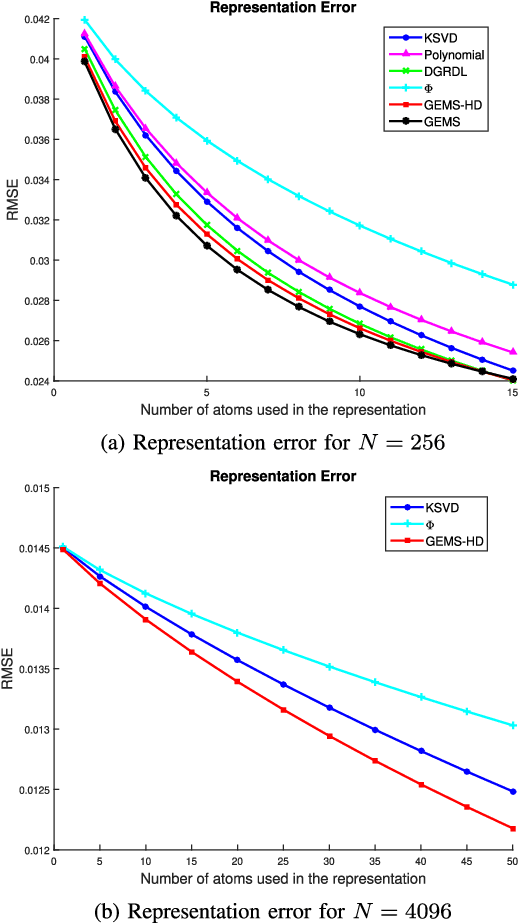
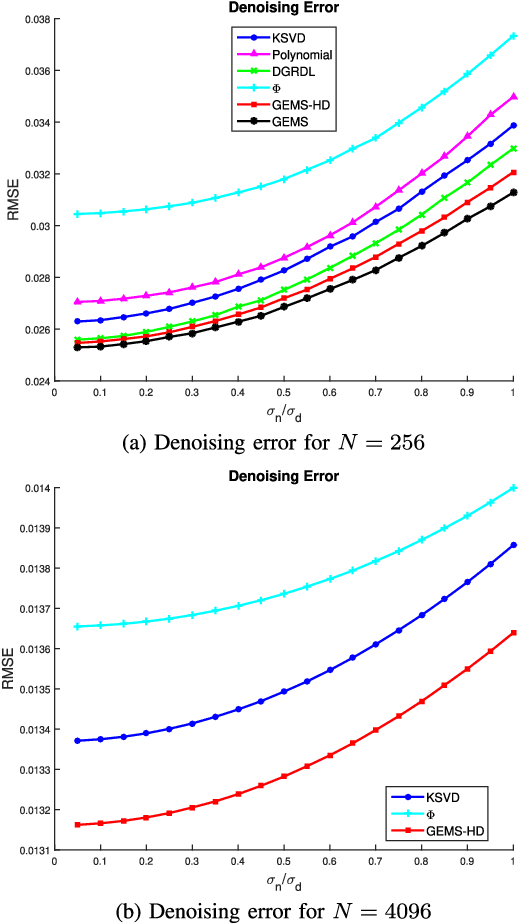
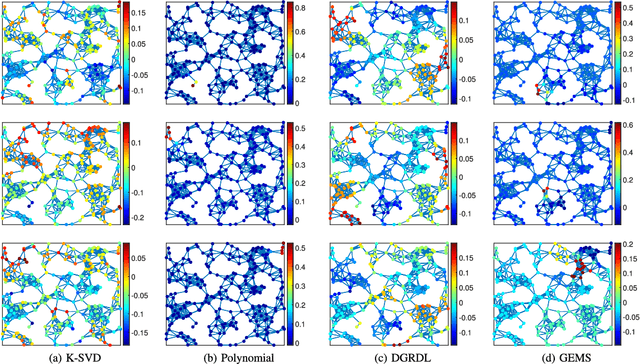
Modern data introduces new challenges to classic signal processing approaches, leading to a growing interest in the field of graph signal processing. A powerful and well established model for real world signals in various domains is sparse representation over a dictionary, combined with the ability to train the dictionary from signal examples. This model has been successfully applied to graph signals as well by integrating the underlying graph topology into the learned dictionary. Nonetheless, dictionary learning methods for graph signals are typically restricted to small dimensions due to the computational constraints that the dictionary learning problem entails, and due to the direct use of the graph Laplacian matrix. In this paper, we propose a dictionary learning algorithm that applies to a broader class of graph signals, and is capable of handling much higher dimensional data. We incorporate the underlying graph topology both implicitly, by forcing the learned dictionary atoms to be sparse combinations of graph-wavelet functions, and explicitly, by adding direct graph constraints to promote smoothness in both the feature and manifold domains. The resulting atoms are thus adapted to the data of interest while adhering to the underlying graph structure and possessing a desired multi-scale property. Experimental results on several datasets, representing both synthetic and real network data of different nature, demonstrate the effectiveness of the proposed algorithm for graph signal processing even in high dimensions.

Structure-Aware Classification using Supervised Dictionary Learning

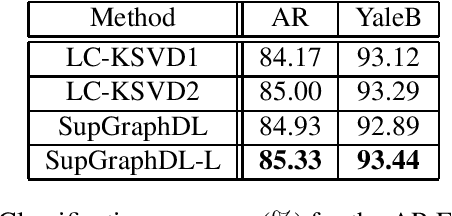
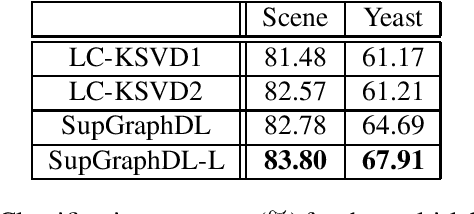
In this paper, we propose a supervised dictionary learning algorithm that aims to preserve the local geometry in both dimensions of the data. A graph-based regularization explicitly takes into account the local manifold structure of the data points. A second graph regularization gives similar treatment to the feature domain and helps in learning a more robust dictionary. Both graphs can be constructed from the training data or learned and adapted along the dictionary learning process. The combination of these two terms promotes the discriminative power of the learned sparse representations and leads to improved classification accuracy. The proposed method was evaluated on several different datasets, representing both single-label and multi-label classification problems, and demonstrated better performance compared with other dictionary based approaches.

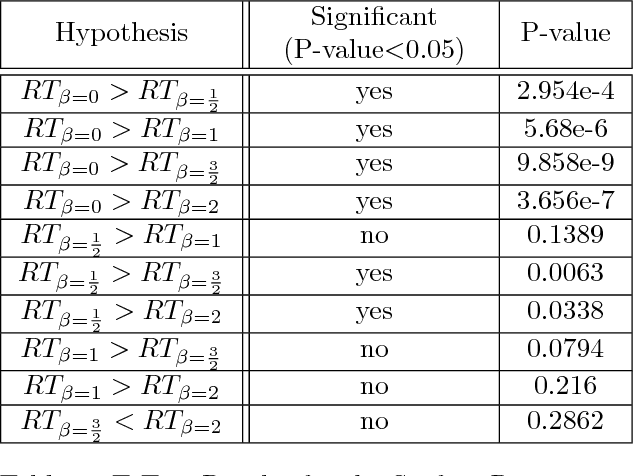
Depth Perception in Autostereograms: 1/f-Noise is Best

An autostereogram is a single image that encodes depth information that pops out when looking at it. The trick is achieved by replicating a vertical strip that sets a basic two-dimensional pattern with disparity shifts that encode a three-dimensional scene. It is of interest to explore the dependency between the ease of perceiving depth in autostereograms and the choice of the basic pattern used for generating them. In this work we confirm a theory proposed by Bruckstein et al. to explain the process of autostereographic depth perception, providing a measure for the ease of "locking into" the depth profile, based on the spectral properties of the basic pattern used. We report the results of three sets of psychophysical experiments using autostereograms generated from two-dimensional random noise patterns having power spectra of the form $1/f^\beta$. The experiments were designed to test the ability of human subjects to identify smooth, low resolution surfaces, as well as detail, in the form of higher resolution objects in the depth profile, and to determine limits in identifying small objects as a function of their size. In accordance with the theory, we discover a significant advantage of the $1/f$ noise pattern (pink noise) for fast depth lock-in and fine detail detection, showing that such patterns are optimal choices for autostereogram design. Validating the theoretical model predictions strengthens its underlying assumptions, and contributes to a better understanding of the visual system's binocular disparity mechanisms.