Neural Graduated Assignment for Maximum Common Edge Subgraphs

The Maximum Common Edge Subgraph (MCES) problem is a crucial challenge with significant implications in domains such as biology and chemistry. Traditional approaches, which include transformations into max-clique and search-based algorithms, suffer from scalability issues when dealing with larger instances. This paper introduces ``Neural Graduated Assignment'' (NGA), a simple, scalable, unsupervised-training-based method that addresses these limitations by drawing inspiration from the classical Graduated Assignment (GA) technique. Central to NGA is stacking of neural components that closely resemble the GA process, but with the reparameterization of learnable temperature into higher dimension. We further theoretically analyze the learning dynamics of NGA, showing its design leads to fast convergence, better exploration-exploitation tradeoff, and ability to escape local optima. Extensive experiments across MCES computation, graph similarity estimation, and graph retrieval tasks reveal that NGA not only significantly improves computation time and scalability on large instances but also enhances performance compared to existing methodologies. The introduction of NGA marks a significant advancement in the computation of MCES and offers insights into other assignment problems.

Hidden Markov Models for Pipeline Damage Detection Using Piezoelectric Transducers

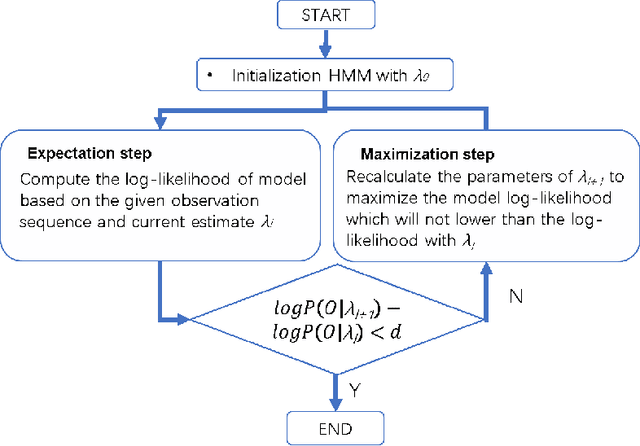
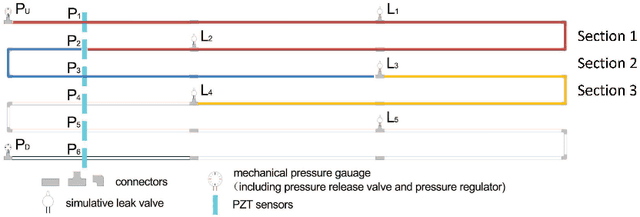
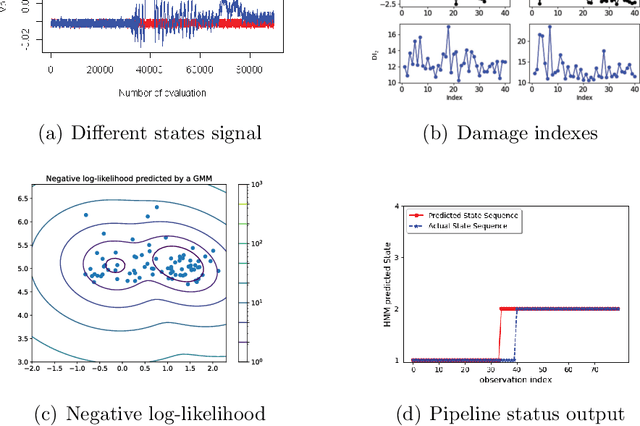
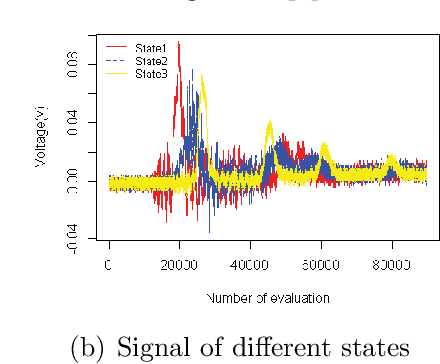
Oil and gas pipeline leakages lead to not only enormous economic loss but also environmental disasters. How to detect the pipeline damages including leakages and cracks has attracted much research attention. One of the promising leakage detection method is to use lead zirconate titanate (PZT) transducers to detect the negative pressure wave when leakage occurs. PZT transducers can generate and detect guided stress waves for crack detection also. However, the negative pressure waves or guided stress waves may not be easily detected with environmental interference, e.g., the oil and gas pipelines in offshore environment. In this paper, a Gaussian mixture model based hidden Markov model (GMM-HMM) method is proposed to detect the pipeline leakage and crack depth in changing environment and time-varying operational conditions. Leakages in different sections or crack depths are considered as different states in hidden Markov models (HMM). Laboratory experiments show that the GMM-HMM method can recognize the crack depth and leakage of pipeline such as whether there is a leakage, where the leakage is.