Xuanyuan Luo
Make It Long, Keep It Fast: End-to-End 10k-Sequence Modeling at Billion Scale on Douyin
Nov 08, 2025



Abstract:Short-video recommenders such as Douyin must exploit extremely long user histories without breaking latency or cost budgets. We present an end-to-end system that scales long-sequence modeling to 10k-length histories in production. First, we introduce Stacked Target-to-History Cross Attention (STCA), which replaces history self-attention with stacked cross-attention from the target to the history, reducing complexity from quadratic to linear in sequence length and enabling efficient end-to-end training. Second, we propose Request Level Batching (RLB), a user-centric batching scheme that aggregates multiple targets for the same user/request to share the user-side encoding, substantially lowering sequence-related storage, communication, and compute without changing the learning objective. Third, we design a length-extrapolative training strategy -- train on shorter windows, infer on much longer ones -- so the model generalizes to 10k histories without additional training cost. Across offline and online experiments, we observe predictable, monotonic gains as we scale history length and model capacity, mirroring the scaling law behavior observed in large language models. Deployed at full traffic on Douyin, our system delivers significant improvements on key engagement metrics while meeting production latency, demonstrating a practical path to scaling end-to-end long-sequence recommendation to the 10k regime.
Generalization Bounds for Gradient Methods via Discrete and Continuous Prior
Jun 01, 2022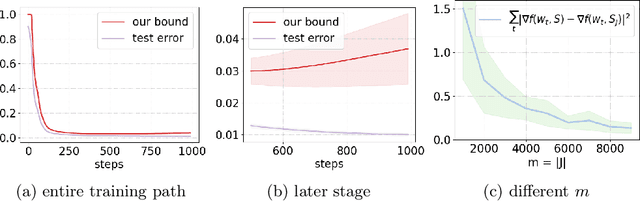
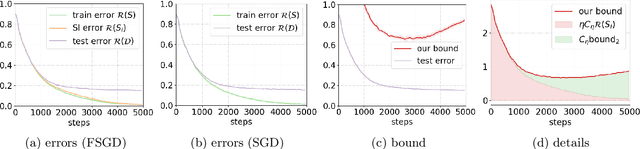
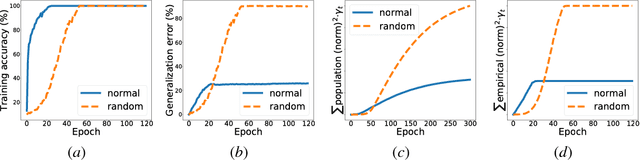
Abstract:Proving algorithm-dependent generalization error bounds for gradient-type optimization methods has attracted significant attention recently in learning theory. However, most existing trajectory-based analyses require either restrictive assumptions on the learning rate (e.g., fast decreasing learning rate), or continuous injected noise (such as the Gaussian noise in Langevin dynamics). In this paper, we introduce a new discrete data-dependent prior to the PAC-Bayesian framework, and prove a high probability generalization bound of order $O(\frac{1}{n}\cdot \sum_{t=1}^T(\gamma_t/\varepsilon_t)^2\left\|{\mathbf{g}_t}\right\|^2)$ for Floored GD (i.e. a version of gradient descent with precision level $\varepsilon_t$), where $n$ is the number of training samples, $\gamma_t$ is the learning rate at step $t$, $\mathbf{g}_t$ is roughly the difference of the gradient computed using all samples and that using only prior samples. $\left\|{\mathbf{g}_t}\right\|$ is upper bounded by and and typical much smaller than the gradient norm $\left\|{\nabla f(W_t)}\right\|$. We remark that our bound holds for nonconvex and nonsmooth scenarios. Moreover, our theoretical results provide numerically favorable upper bounds of testing errors (e.g., $0.037$ on MNIST). Using a similar technique, we can also obtain new generalization bounds for certain variants of SGD. Furthermore, we study the generalization bounds for gradient Langevin Dynamics (GLD). Using the same framework with a carefully constructed continuous prior, we show a new high probability generalization bound of order $O(\frac{1}{n} + \frac{L^2}{n^2}\sum_{t=1}^T(\gamma_t/\sigma_t)^2)$ for GLD. The new $1/n^2$ rate is due to the concentration of the difference between the gradient of training samples and that of the prior.
On Generalization Error Bounds of Noisy Gradient Methods for Non-Convex Learning
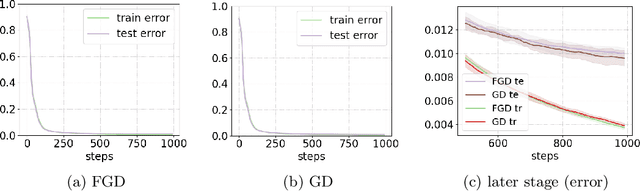
Feb 02, 2019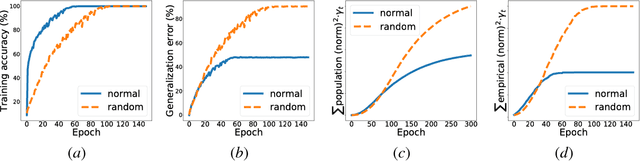
Abstract:Generalization error (also known as the out-of-sample error) measures how well the hypothesis obtained from the training data can generalize to previously unseen data. Obtaining tight generalization error bounds is central to statistical learning theory. In this paper, we study the generalization error bound in learning general non-convex objectives, which has attracted significant attention in recent years. In particular, we study the (algorithm-dependent) generalization bounds of various iterative gradient based methods. (1) We present a very simple and elementary proof of a recent result for stochastic gradient Langevin dynamics (SGLD), due to Mou et al. (2018). Our proof can be easily extended to obtain similar generalization bounds for several other variants of SGLD (e.g., with postprocessing, momentum, mini-batch, acceleration, and more general noises), and improves upon the recent results in Pensia et al. (2018). (2) By incorporating ideas from the PAC-Bayesian theory into the stability framework, we obtain tighter distribution-dependent (or data-dependent) generalization bounds. Our bounds provide an intuitive explanation for the phenomenon reported in Zhang et al. (2017a). (3) We also study the setting where the total loss is the sum of a bounded loss and an additional `l2 regularization term. We obtain new generalization bounds for the continuous Langevin dynamic in this setting by leveraging the tool of Log-Sobolev inequality. Our new bounds are more desirable when the noisy level of the process is not small, and do not grow when T approaches to infinity.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge