Variational Approximations between Mean Field Theory and the Junction Tree Algorithm

Recently, variational approximations such as the mean field approximation have received much interest. We extend the standard mean field method by using an approximating distribution that factorises into cluster potentials. This includes undirected graphs, directed acyclic graphs and junction trees. We derive generalized mean field equations to optimize the cluster potentials. We show that the method bridges the gap between the standard mean field approximation and the exact junction tree algorithm. In addition, we address the problem of how to choose the graphical structure of the approximating distribution. From the generalised mean field equations we derive rules to simplify the structure of the approximating distribution in advance without affecting the quality of the approximation. We also show how the method fits into some other variational approximations that are currently popular.

IPF for Discrete Chain Factor Graphs

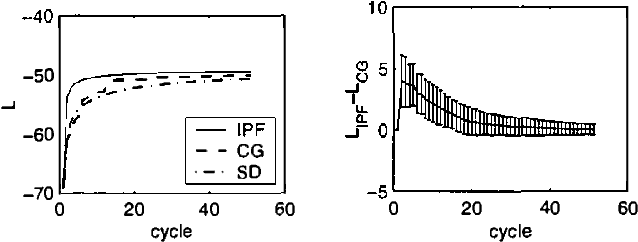
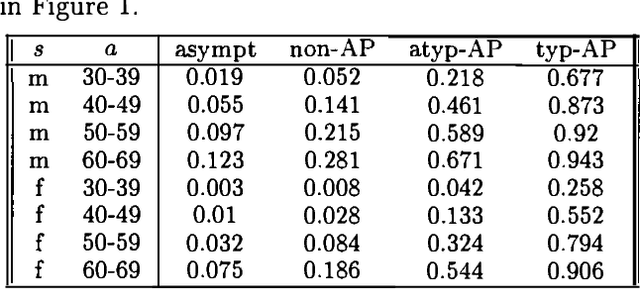
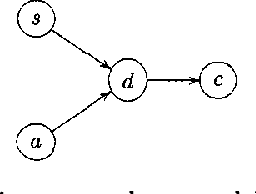
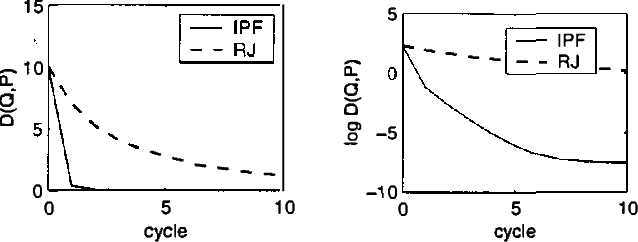
Iterative Proportional Fitting (IPF), combined with EM, is commonly used as an algorithm for likelihood maximization in undirected graphical models. In this paper, we present two iterative algorithms that generalize upon IPF. The first one is for likelihood maximization in discrete chain factor graphs, which we define as a wide class of discrete variable models including undirected graphical models and Bayesian networks, but also chain graphs and sigmoid belief networks. The second one is for conditional likelihood maximization in standard undirected models and Bayesian networks. In both algorithms, the iteration steps are expressed in closed form. Numerical simulations show that the algorithms are competitive with state of the art methods.