Understanding the role of depth in the neural tangent kernel for overparameterized neural networks

Overparameterized fully-connected neural networks have been shown to behave like kernel models when trained with gradient descent, under mild conditions on the width, the learning rate, and the parameter initialization. In the limit of infinitely large widths and small learning rate, the kernel that is obtained allows to represent the output of the learned model with a closed-form solution. This closed-form solution hinges on the invertibility of the limiting kernel, a property that often holds on real-world datasets. In this work, we analyze the sensitivity of large ReLU networks to increasing depths by characterizing the corresponding limiting kernel. Our theoretical results demonstrate that the normalized limiting kernel approaches the matrix of ones. In contrast, they show the corresponding closed-form solution approaches a fixed limit on the sphere. We empirically evaluate the order of magnitude in network depth required to observe this convergent behavior, and we describe the essential properties that enable the generalization of our results to other kernels.

Design and Implementation of an Heuristic-Enhanced Branch-and-Bound Solver for MILP

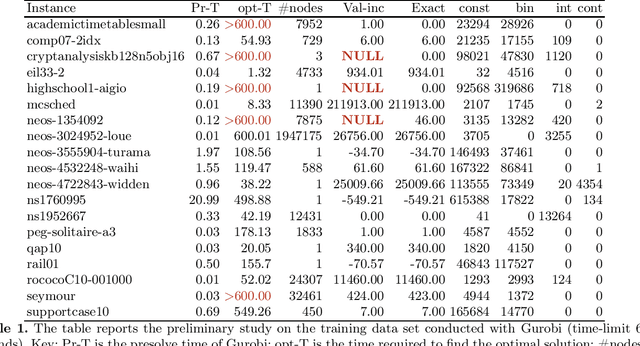
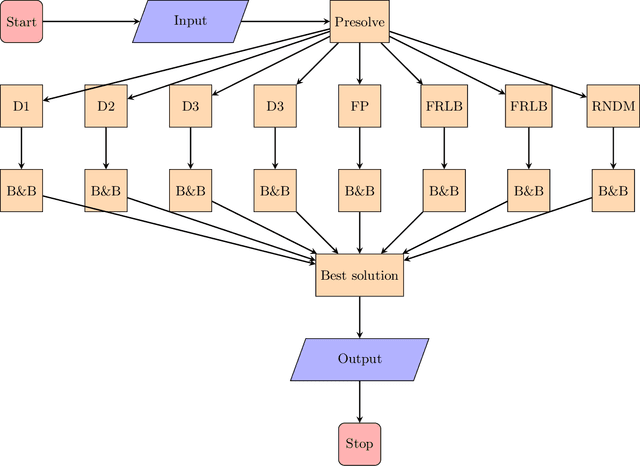
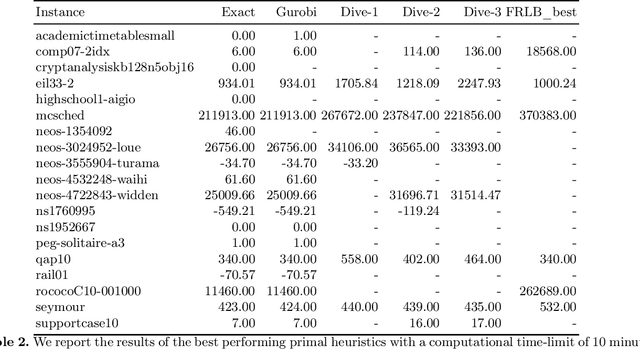
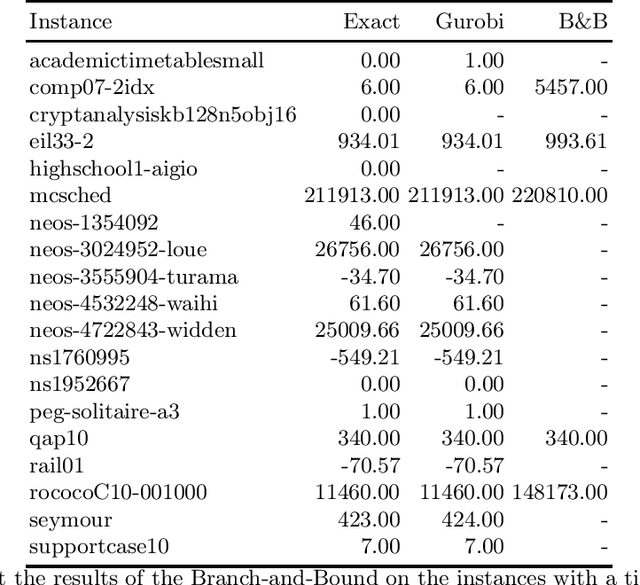
We present a solver for Mixed Integer Programs (MIP) developed for the MIP competition 2022. Given the 10 minutes bound on the computational time established by the rules of the competition, our method focuses on finding a feasible solution and improves it through a Branch-and-Bound algorithm. Another rule of the competition allows the use of up to 8 threads. Each thread is given a different primal heuristic, which has been tuned by hyper-parameters, to find a feasible solution. In every thread, once a feasible solution is found, we stop and we use a Branch-and-Bound method, embedded with local search heuristics, to ameliorate the incumbent solution. The three variants of the Diving heuristic that we implemented manage to find a feasible solution for 10 instances of the training data set. These heuristics are the best performing among the heuristics that we implemented. Our Branch-and-Bound algorithm is effective on a small portion of the training data set, and it manages to find an incumbent feasible solution for an instance that we could not solve with the Diving heuristics. Overall, our combined methods, when implemented with extensive computational power, can solve 11 of the 19 problems of the training data set within the time limit. Our submission to the MIP competition was awarded the "Outstanding Student Submission" honorable mention.