Learning richness modulates equality reasoning in neural networks

Equality reasoning is ubiquitous and purely abstract: sameness or difference may be evaluated no matter the nature of the underlying objects. As a result, same-different tasks (SD) have been extensively studied as a starting point for understanding abstract reasoning in humans and across animal species. With the rise of neural networks (NN) that exhibit striking apparent proficiency for abstractions, equality reasoning in NNs has also gained interest. Yet despite extensive study, conclusions about equality reasoning vary widely and with little consensus. To clarify the underlying principles in learning SD, we develop a theory of equality reasoning in multi-layer perceptrons (MLP). Following observations in comparative psychology, we propose a spectrum of behavior that ranges from conceptual to perceptual outcomes. Conceptual behavior is characterized by task-specific representations, efficient learning, and insensitivity to spurious perceptual details. Perceptual behavior is characterized by strong sensitivity to spurious perceptual details, accompanied by the need for exhaustive training to learn the task. We develop a mathematical theory to show that an MLP's behavior is driven by learning richness. Rich-regime MLPs exhibit conceptual behavior, whereas lazy-regime MLPs exhibit perceptual behavior. We validate our theoretical findings in vision SD experiments, showing that rich feature learning promotes success by encouraging hallmarks of conceptual behavior. Overall, our work identifies feature learning richness as a key parameter modulating equality reasoning, and suggests that equality reasoning in humans and animals may similarly depend on learning richness in neural circuits.

No Free Lunch From Random Feature Ensembles

Given a budget on total model size, one must decide whether to train a single, large neural network or to combine the predictions of many smaller networks. We study this trade-off for ensembles of random-feature ridge regression models. We prove that when a fixed number of trainable parameters are partitioned among $K$ independently trained models, $K=1$ achieves optimal performance, provided the ridge parameter is optimally tuned. We then derive scaling laws which describe how the test risk of an ensemble of regression models decays with its total size. We identify conditions on the kernel and task eigenstructure under which ensembles can achieve near-optimal scaling laws. Training ensembles of deep convolutional neural networks on CIFAR-10 and a transformer architecture on C4, we find that a single large network outperforms any ensemble of networks with the same total number of parameters, provided the weight decay and feature-learning strength are tuned to their optimal values.

MLPs Learn In-Context

In-context learning (ICL), the remarkable ability to solve a task from only input exemplars, has commonly been assumed to be a unique hallmark of Transformer models. In this study, we demonstrate that multi-layer perceptrons (MLPs) can also learn in-context. Moreover, we find that MLPs, and the closely related MLP-Mixer models, learn in-context competitively with Transformers given the same compute budget. We further show that MLPs outperform Transformers on a subset of ICL tasks designed to test relational reasoning. These results suggest that in-context learning is not exclusive to Transformers and highlight the potential of exploring this phenomenon beyond attention-based architectures. In addition, MLPs' surprising success on relational tasks challenges prior assumptions about simple connectionist models. Altogether, our results endorse the broad trend that ``less inductive bias is better" and contribute to the growing interest in all-MLP alternatives to task-specific architectures.

Contrasting random and learned features in deep Bayesian linear regression

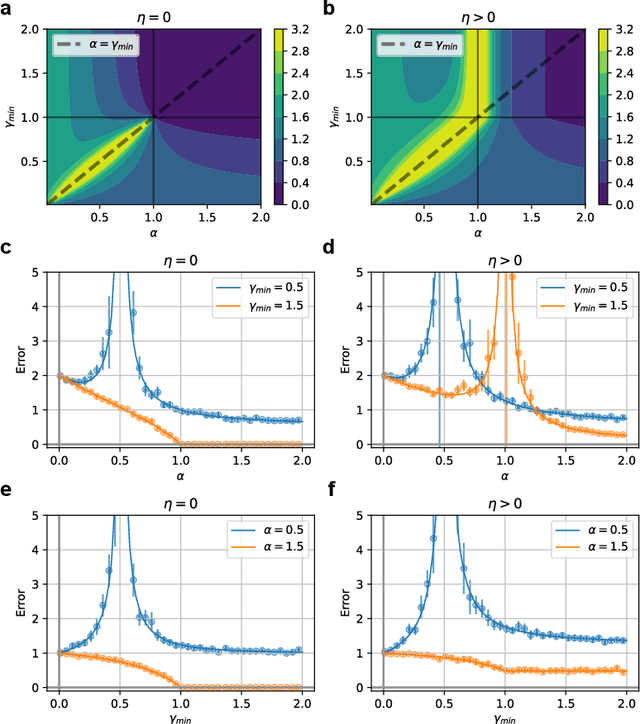
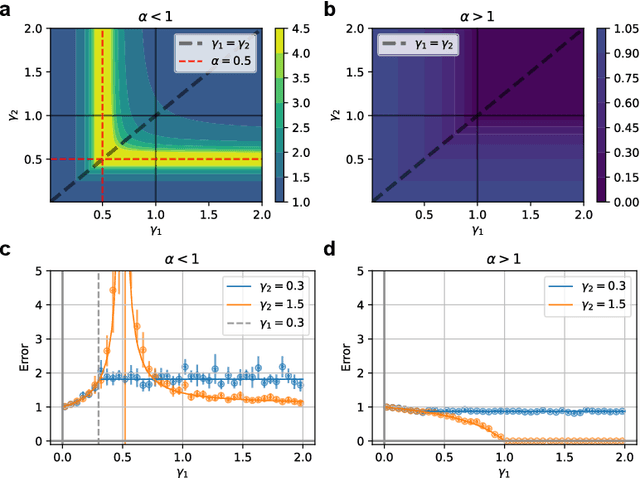
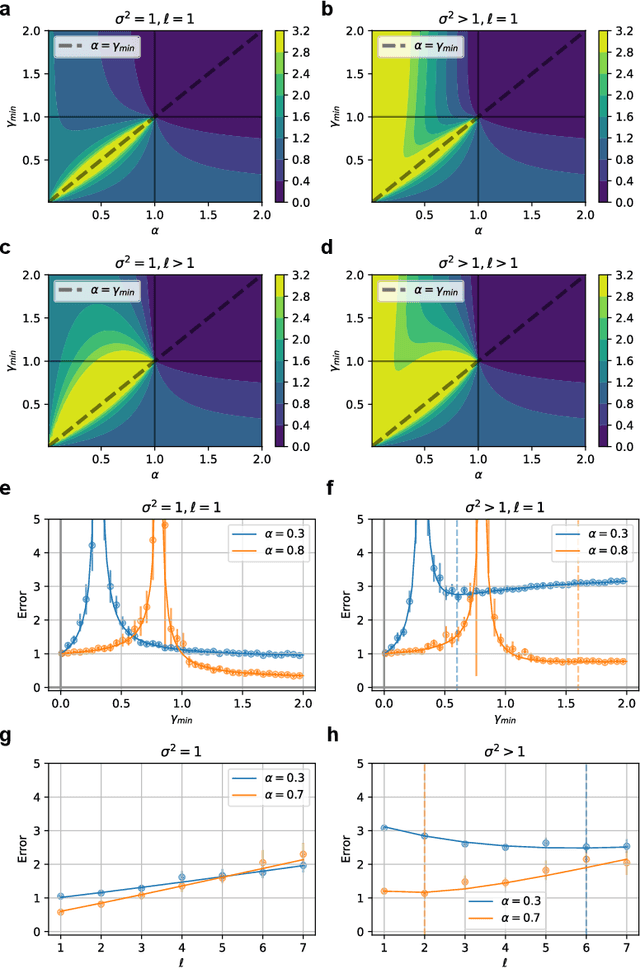
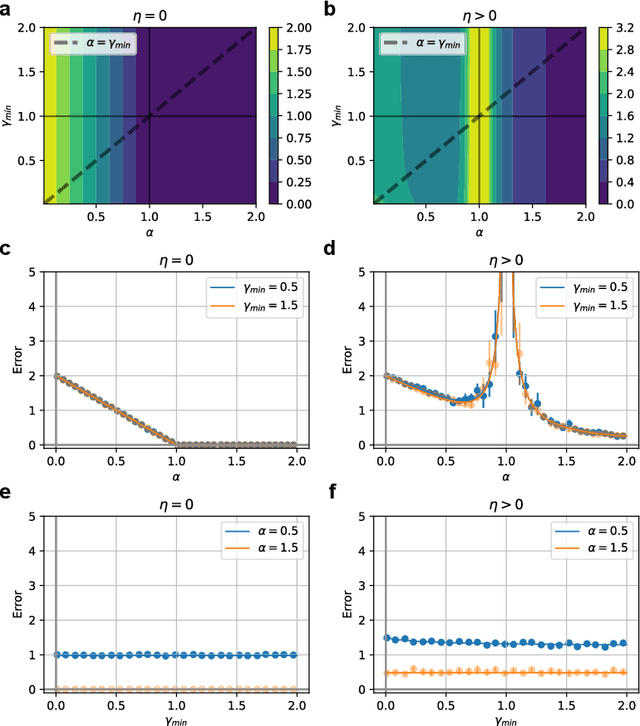
Understanding how feature learning affects generalization is among the foremost goals of modern deep learning theory. Here, we study how the ability to learn representations affects the generalization performance of a simple class of models: deep Bayesian linear neural networks trained on unstructured Gaussian data. By comparing deep random feature models to deep networks in which all layers are trained, we provide a detailed characterization of the interplay between width, depth, data density, and prior mismatch. We show that both models display sample-wise double-descent behavior in the presence of label noise. Random feature models can also display model-wise double-descent if there are narrow bottleneck layers, while deep networks do not show these divergences. Random feature models can have particular widths that are optimal for generalization at a given data density, while making neural networks as wide or as narrow as possible is always optimal. Moreover, we show that the leading-order correction to the kernel-limit learning curve cannot distinguish between random feature models and deep networks in which all layers are trained. Taken together, our findings begin to elucidate how architectural details affect generalization performance in this simple class of deep regression models.