Sparsification and Reconstruction from the Perspective of Representation Geometry

Sparse Autoencoders (SAEs) have emerged as a predominant tool in mechanistic interpretability, aiming to identify interpretable monosemantic features. However, how does sparse encoding organize the representations of activation vector from language models? What is the relationship between this organizational paradigm and feature disentanglement as well as reconstruction performance? To address these questions, we propose the SAEMA, which validates the stratified structure of the representation by observing the variability of the rank of the symmetric semipositive definite (SSPD) matrix corresponding to the modal tensor unfolded along the latent tensor with the level of noise added to the residual stream. To systematically investigate how sparse encoding alters representational structures, we define local and global representations, demonstrating that they amplify inter-feature distinctions by merging similar semantic features and introducing additional dimensionality. Furthermore, we intervene the global representation from an optimization perspective, proving a significant causal relationship between their separability and the reconstruction performance. This study explains the principles of sparsity from the perspective of representational geometry and demonstrates the impact of changes in representational structure on reconstruction performance. Particularly emphasizes the necessity of understanding representations and incorporating representational constraints, providing empirical references for developing new interpretable tools and improving SAEs. The code is available at \hyperlink{https://github.com/wenjie1835/SAERepGeo}{https://github.com/wenjie1835/SAERepGeo}.

A Fast Matrix-Completion-Based Approach for Recommendation Systems

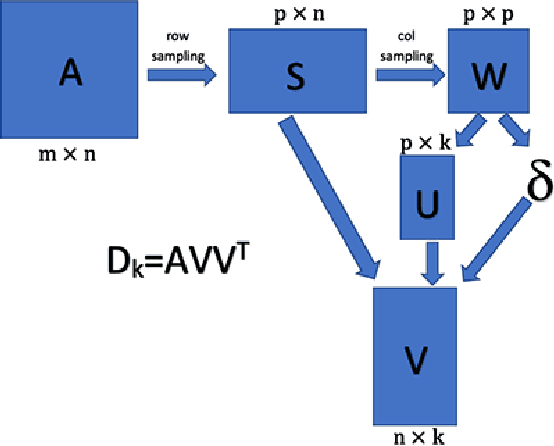
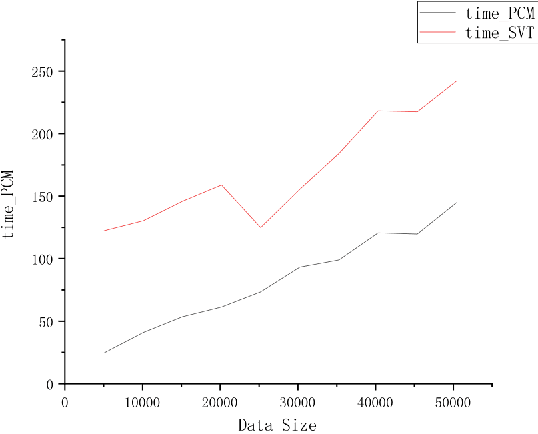
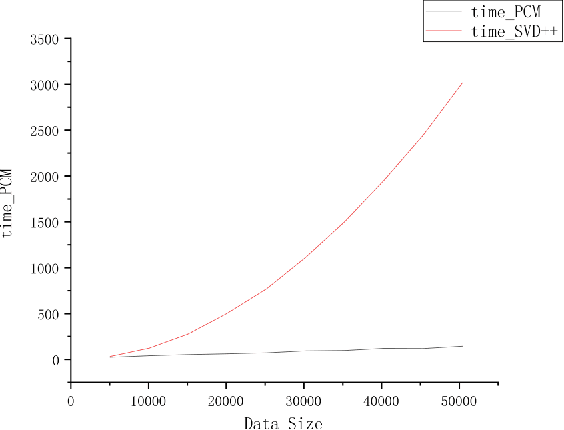
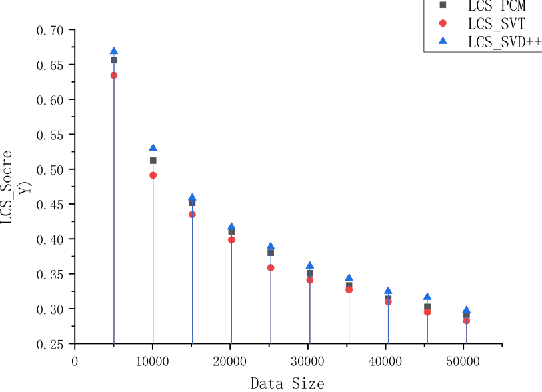
Matrix completion is widely used in machine learning, engineering control, image processing, and recommendation systems. Currently, a popular algorithm for matrix completion is Singular Value Threshold (SVT). In this algorithm, the singular value threshold should be set first. However, in a recommendation system, the dimension of the preference matrix keeps changing. Therefore, it is difficult to directly apply SVT. In addition, what the users of a recommendation system need is a sequence of personalized recommended results rather than the estimation of their scores. According to the above ideas, this paper proposes a novel approach named probability completion model~(PCM). By reducing the data dimension, the transitivity of the similar matrix, and singular value decomposition, this approach quickly obtains a completion matrix with the same probability distribution as the original matrix. The approach greatly reduces the computation time based on the accuracy of the sacrifice part, and can quickly obtain a low-rank similarity matrix with data trend approximation properties. The experimental results show that PCM can quickly generate a complementary matrix with similar data trends as the original matrix. The LCS score and efficiency of PCM are both higher than SVT.